AVL 平衡树的旋转理解
AVL 平衡树的完全代码见 https://www.cnblogs.com/fanlumaster/p/13824006.html
首先我们明确一个定义:平衡因子:树的一个节点的左、右子树的高度差称为该节点的平衡因子。一棵 AVL 树的平衡因子只能有 0、-1、1 三种取值。
单旋转
LL 情况下的单旋转
左边是旋转前,右边是旋转后
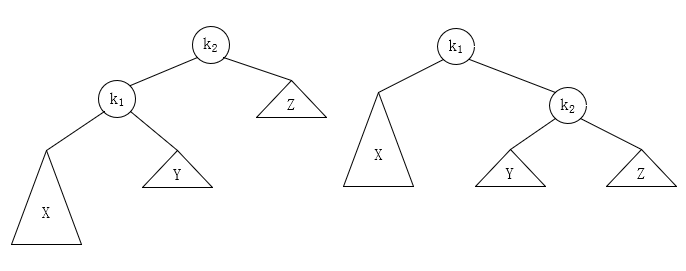
LL情况:插入一个新节点到根节点的左子树(Left)的左子树(Left),导致根节点的平衡因子由 1 变为 2,如上图,在根节点 \(k_2\) 的左子树的左边插入节点 \(X\),导致 \(k_2\) 的平衡因子由 1 变成了 2。
为使树恢复平衡,我们把 \(k_1\) 变成这棵树的新根节点,因为 \(k_2\) 大于 \(k_1\),所以把 \(k_2\) 置为 \(k_1\) 的右子树,而原本在 \(k_1\) 的右子树的 \(Y\) 大于 \(k_1\) 且小于 \(k_2\),所以我们需要把 \(Y\) 置为 \(k_2\) 的左子树。这样一来,这棵树就重新恢复平衡。
简单来讲,我们只需要把 \(k_1\) 给“拎”上去,然后再把 \(Y\) 转移到 \(k_2\) 的左子树的位置就可以了。
一个旋转样例:
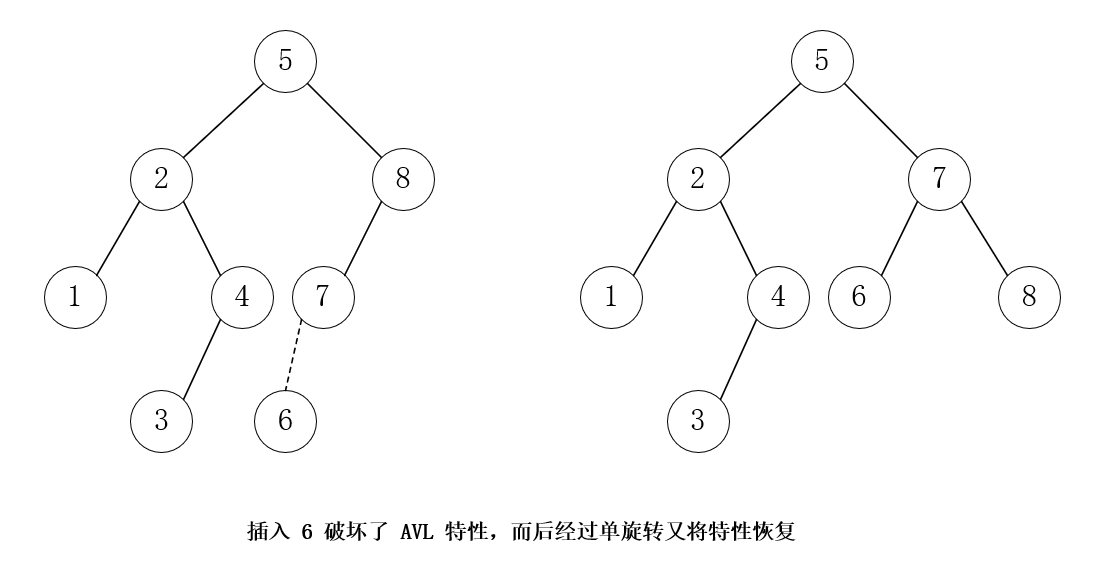
代码:
/* This function can be called only if K2 has a left child */
/* Perform a rotate between a node (K2) and its left child */
/* Update heights, then return new root */
// LL 单旋转
static Position
SingleRotateWithLeft(Position K2)
{
Position K1;
// 旋转操作
K1 = K2->Left;
K2->Left = K1->Right;
K1->Right = K2;
// 更新节点的高度
K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1;
K1->Height = Max(Height(K1->Left), K2->Height) + 1;
return K1; /* New root 新的根节点 */
}
RR 情况下的单旋转
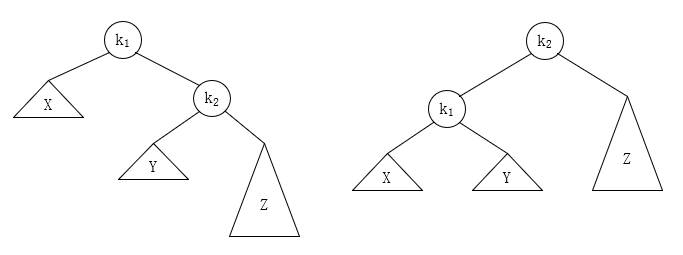
RR情况:和上面的类似,相当于对称的情况。
简单理解就是,把 \(k_2\) 给“拎”上去,然后 \(Y\) 根据相应的情况转移到 \(k_1\) 的右子树位置上。
代码:
/* This function can be called only if K1 has a right child */
/* Perform a rotate between a node (K1) and its right child */
/* Update heights, then return new root */
// RR 单旋转
static Position
SingleRotateWithRight(Position K1)
{
Position K2;
// 旋转操作
K2 = K1->Right;
K1->Right = K2->Left;
K2->Left = K1;
// 更新节点高度
K1->Height = Max(Height(K1->Left), Height(K1->Right)) + 1;
K2->Height = Max(Height(K2->Right), K1->Height) + 1;
return K2; /* New root */
}
双旋转
LR 情况下的双旋转
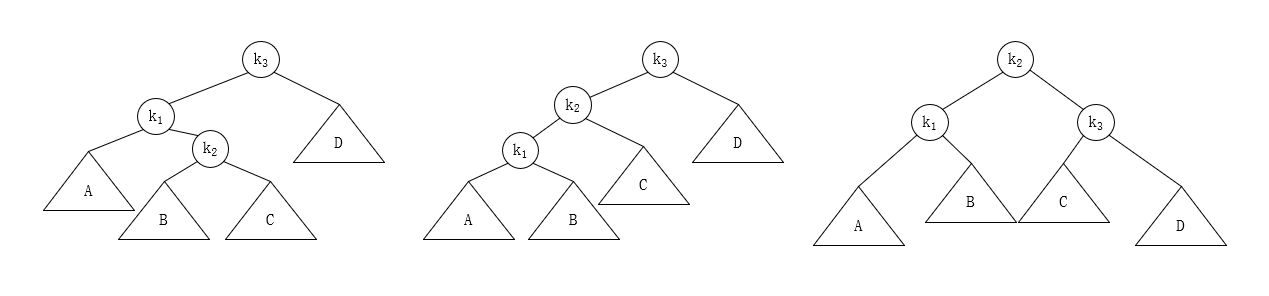
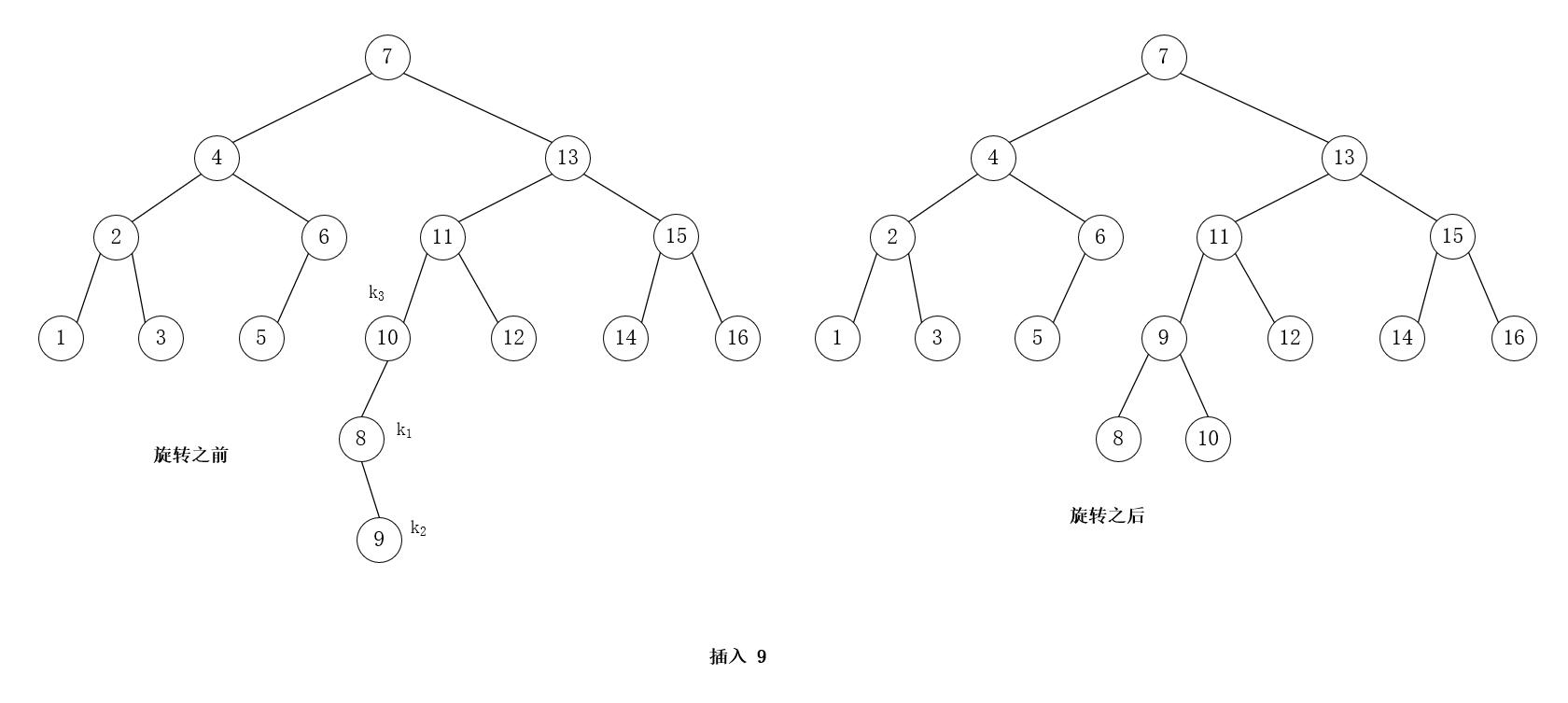
结合上面的图解,可以发现,LR 情况下的双旋转其实是两个单旋转:
- 先对 \(k_1\) 进行 RR 单旋转,即,把 \(k_2\) 给“拎”上来
- 然后对 \(k_3\) 进行 LL 单旋转,即,把 \(k_2\) 给“拎”上来
代码:
/* This function can be called only if K3 has a left */
/* child and K3's left child has a right child */
/* Do the left-right double rotation */
/* Update heights, then return new root */
// LR 双旋转
static Position
DoubleRotateWithLeft(Position K3)
{
/* Rotate between K1 and K2 */
K3->Left = SingleRotateWithRight(K3->Left); // 先进行 RR 旋转
/* Rotate between K3 and K2 */
return SingleRotateWithLeft(K3); // 然后进行 LL 旋转
}
RL 情况下的双旋转
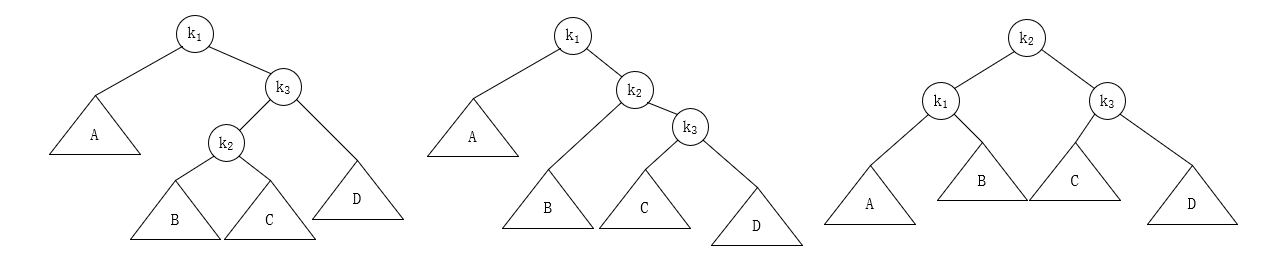
和 LR 类似,RL 情况下的双旋转也是两个单旋转:
- 先对 \(k_3\) 进行 LL 单旋转,把 \(k_2\) 给“拎”上来
- 然后对 \(k_1\) 进行 RR 单旋转,把 \(k_2\) 给“拎”上来
代码:
/* This function can be called only if K1 has a right */
/* child and K1's right child has a left child */
/* Do the right-left double rotation */
/* Update heights, then return new root */
// RL 双旋转
static Position
DoubleRotateWithRight(Position K1)
{
/* Rotate between K3 and K2 */
K1->Right = SingleRotateWithLeft(K1->Right);
/* Rotate between K1 and K2 */
return SingleRotateWithRight(K1);
}
一个例子
插入 3,2,3,在插入 1 的时候进行 LL 单旋转
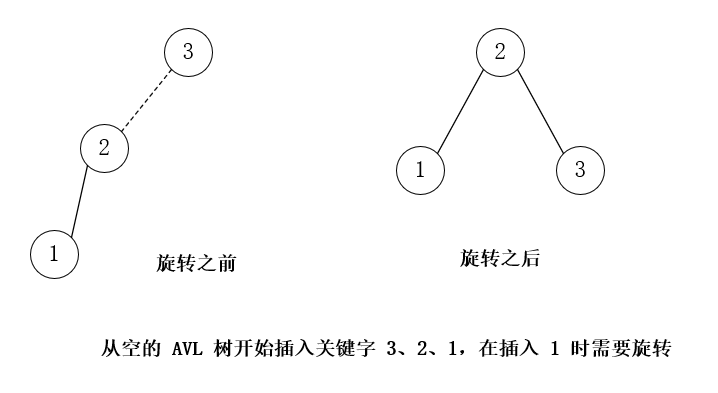
插入 5,RR 单旋转
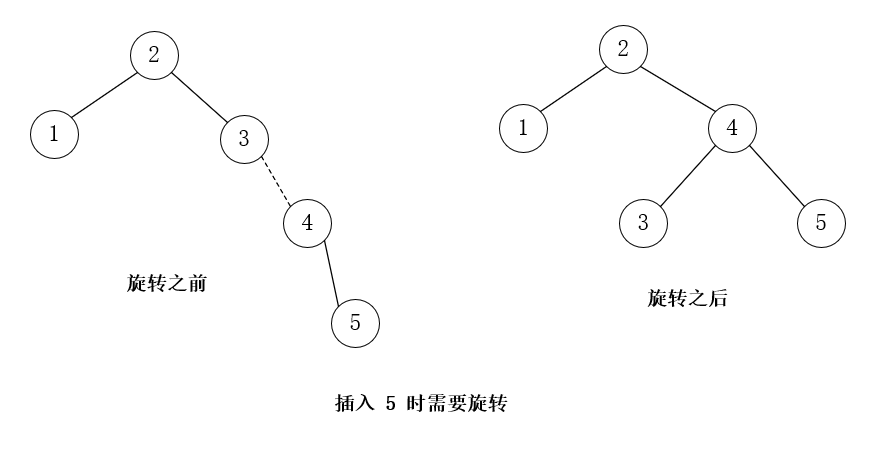
插入 6,RR 单旋转
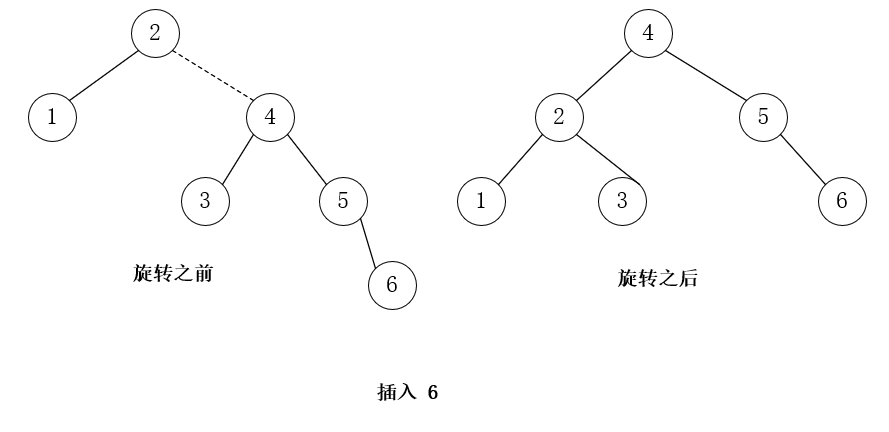
插入 7,RR 单旋转
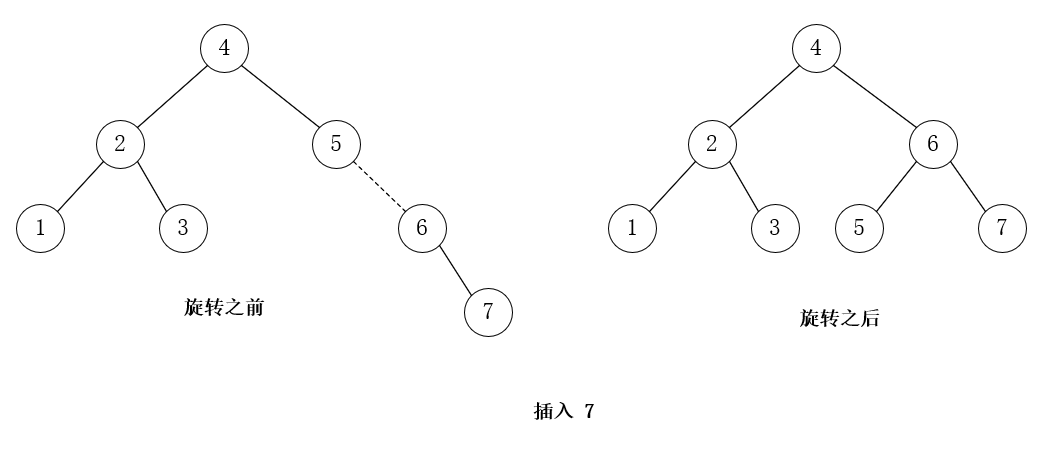
插入 15,16,RL 双旋转
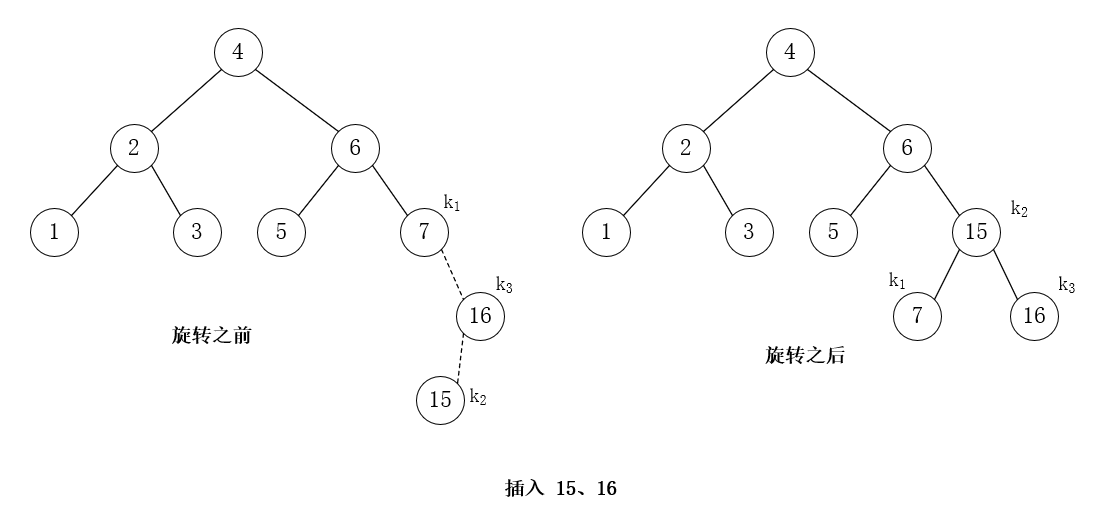
插入 14,RL 双旋转
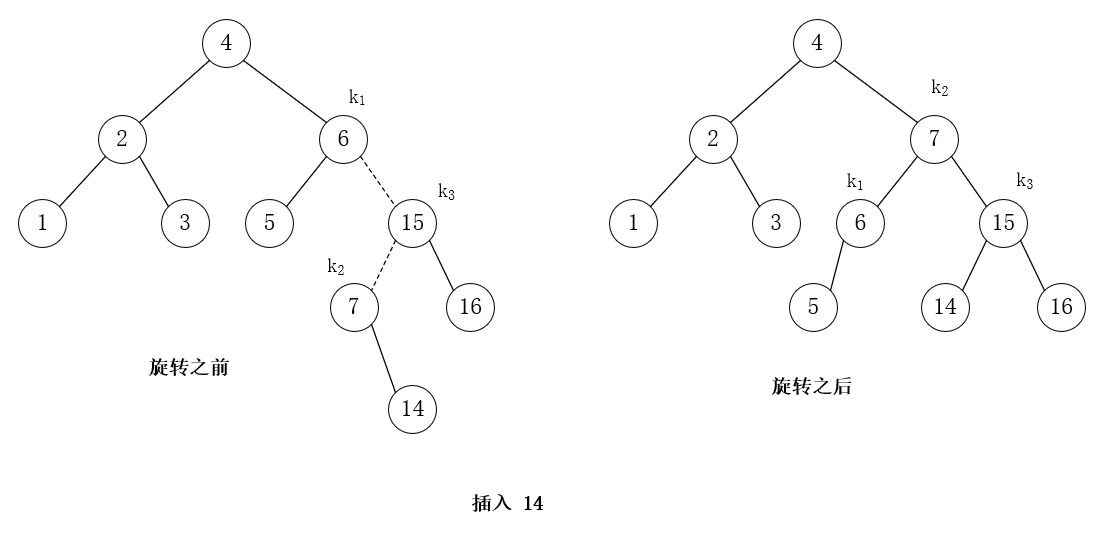
插入 13,RR 单旋转
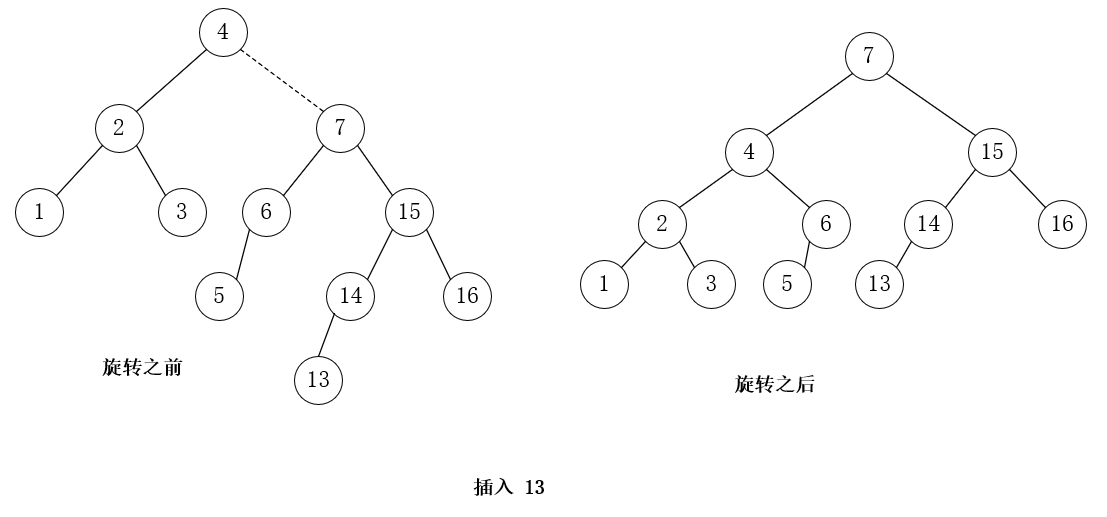
插入 12,LL 单旋转
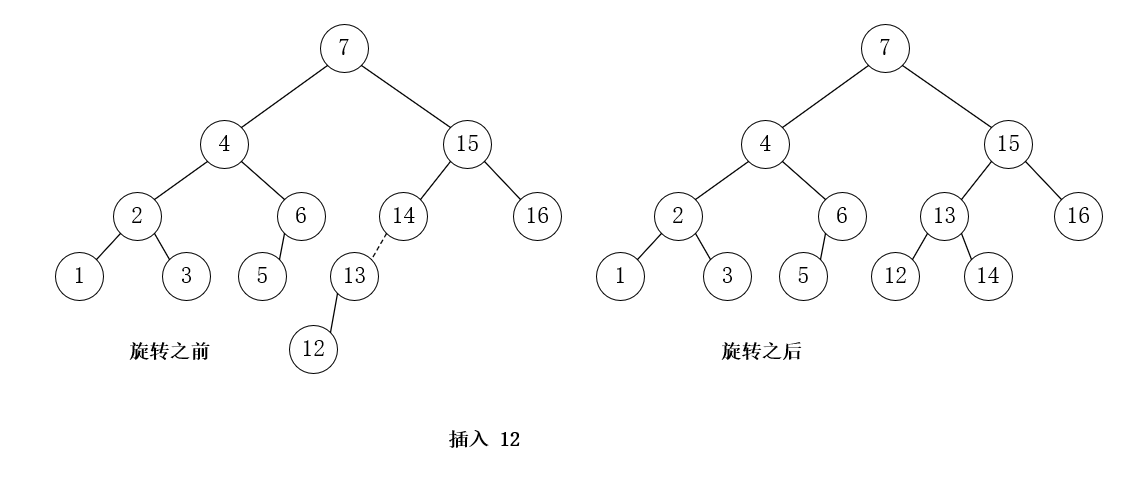
插入 11,10,8,略过过程,其中,插入 11 和 10 都需要单旋转,插入 8 不需要旋转
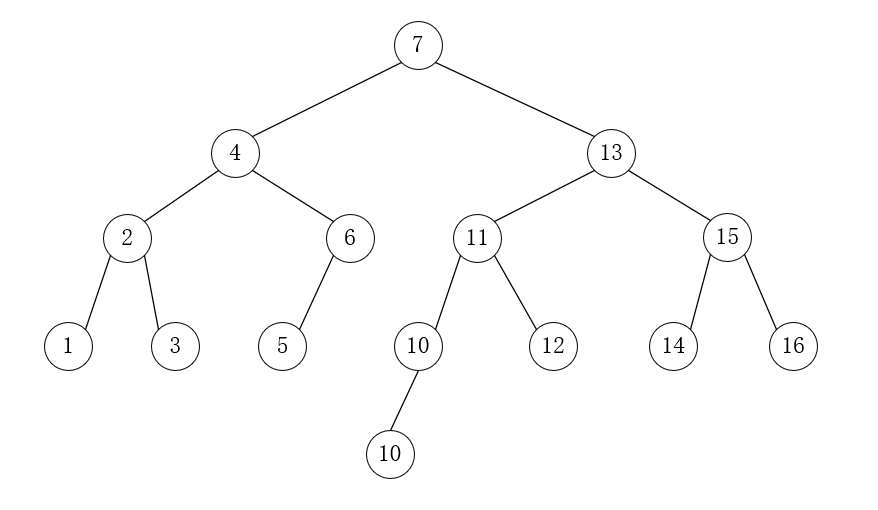
插入 9,LR 双旋转