约瑟夫环问题的两种解法(循环链表和公式法)
问题描述
这里是数据结构课堂上的描述:
- N people form a circle, eliminate a person every k people, who is the final survior?
- Label each person with 0, 1, 2, ..., n - 1, denote(表示,指代) J(n, k) the labels of surviors when there are n people.(J(n, k) 表示了当有 n 个人时幸存者的标号)
- First eliminate the person labeled k - 1, relabel the rest, starting with 0 for the one originally labeled k.
0 1 2 3 ... k-2 k-1 k k+1 ... n-1
... k-2 0 1 ...
Dynamic programming
J(n, k) = J(J(n - 1, k) + k) % n, if n > 1,
J(1, k) = 0
用中文的方式简单翻译一下就是 (吐槽:为啥课上不直接用中文呢?淦!) 有 n 个人围成一圈,从第一个人开始,从 1 开始报数,报 k 的人就将被杀死,然后从下一个人开始重新从 1 开始报数,往后还是报 k 的人被杀掉,杀到最后只剩一个人时,其人就为幸存者。(上面的英文是从 0 开始的,是因为我们写程序时使用了数组,所以下标从 0 开始)
解决方案
循环链表方法
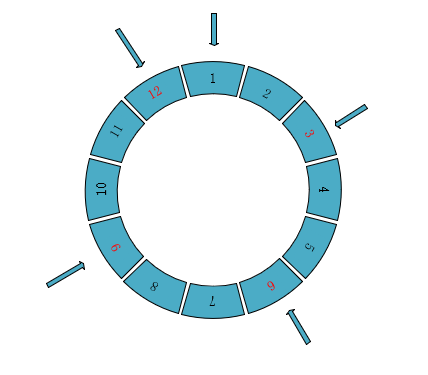
算法思路很简单,我们这里使用了循环链表模拟了这个过程:节点 1 指向节点 2,节点 2 指向节点 3,...,然后节点 N 再指向节点 1,这样就形成了一个圆环。如图所示,n 取 12,k 取 3,从 1 开始报数,然后依次删除 3, 6, 9, 12:
#include<stdio.h>
#include<stdlib.h>
typedef struct Node // 节点存放一个数据和指向下一个节点的指针
{
int data;
struct Node *next;
} *NList; // NList为指向 Node 节点的指针
// 创建一个节点数为 n 的循环链表
NList createList(int n)
{
// 先创建一个节点
NList p, tmp, head;
p = (NList)malloc(sizeof(struct Node));
head = p; // 保存头节点
p->data = 1; // 第一个节点
for (int i = 2; i <=n ; i++)
{
tmp = (NList)malloc(sizeof(struct Node));
tmp->data = i;
p->next = tmp;
p = tmp;
}
p->next = head; // 最后一个节点指回开头
return head;
}
// 从 编号为 1 的人开始报数,报到 k 的人出列,被杀掉
void processList(NList head, int k)
{
if (!head) return;
NList p = head;
NList tmp;
while (p->next != p)
{
for (int i = 0; i < k - 1; i++)
{
tmp = p;
p = p->next;
}
printf("%d 号被杀死\n", p->data);
tmp->next = p->next;
free(p);
p = NULL; // 防止产生野指针,下同
p = tmp->next;
}
printf("幸存者为 %d 号", p->data);
free(p);
p = NULL;
}
int main()
{
NList head = createList(11);
processList(head, 3);
return 0;
}
测试结果:
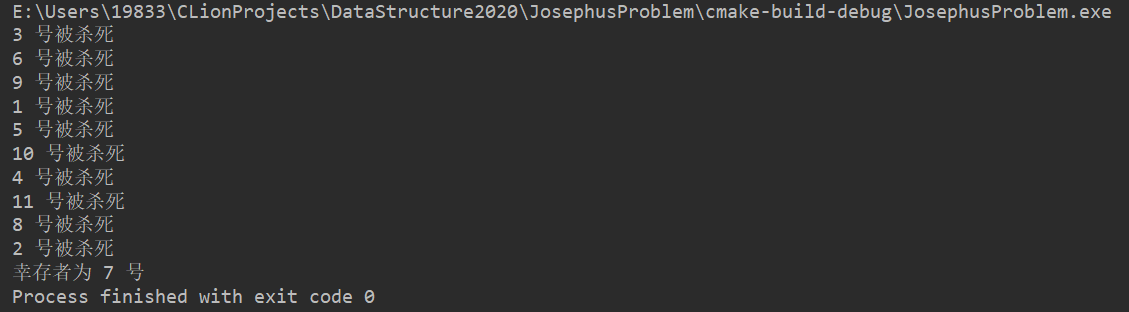
易知,这个算法的时间复杂度为 \(O(nk)\),显然,这不是一个好的算法。
公式法
在问题描述里,我们就有提到公式:
J(n, k) = J(J(n - 1, k) + k) % n, if n > 1,
J(1, k) = 0
下面,我们就来简单证明一下这个算法。
举例,我们用数字表示每一个人:
一共 11 个人,他们排成一排,假设报到 3 的人被杀掉。
- 刚开始时,头一个人编号是1,从他开始报数,第一轮被杀掉的是编号3的人。
- 编号4的人从1开始重新报数,这时候我们可以认为编号4这个人是队伍的头。第二轮被杀掉的是编号6的人。
- 编号7的人开始重新报数,这时候我们可以认为编号7这个人是队伍的头。第三轮被杀掉的是编号9的人。
- ……
- 第九轮时,编号2的人开始重新报数,这时候我们可以认为编号2这个人是队伍的头。这轮被杀掉的是编号8的人。
- 下一个人还是编号为2的人,他从1开始报数,不幸的是他在这轮被杀掉了。
- 最后的胜利者是编号为7的人。
表格演示(表头代表数组的下标):
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 1 | 2 | |
| 7 | 8 | 9 | 10 | 11 | 1 | 2 | 4 | 5 | ||
| 10 | 11 | 1 | 2 | 4 | 5 | 7 | 8 | |||
| 2 | 4 | 5 | 7 | 8 | 10 | 11 | ||||
| 7 | 8 | 10 | 11 | 2 | 4 | |||||
| 11 | 2 | 4 | 7 | 8 | ||||||
| 7 | 8 | 11 | 2 | |||||||
| 2 | 7 | 8 | ||||||||
| 2 | 7 | |||||||||
| 7 |
我们用上面的数据验证一下公式的正确性,其中,J(n, k) 表示的是幸存者在这一轮的下标位置:
- \(J(1, 3) = 0\);只有一个人,此人是最后的幸存者,其在数组中的下标为 0
- \(J(2, 3) = 1 = (J(1, 3) + 3) % 2\);还剩 2 个人时
- \(J(3, 3) = 1 = (J(2, 3) + 3) % 3\);还剩 3 个人时
- \(J(4, 3) = 0 = (J(3, 3) + 3) % 4\)
- \(J(5, 3) = 3 = (J(4, 3) + 3) % 5\)
- ...
- \(J(11, 3) = 6 = (J(10, 3) + 3) % 11\);最终计算出待求的情况
我们通过实例只是验证了这一种情况是成立的,这能够很好地辅助我们理解,但是,我们还需要这个公式的具体推导,下面,就以问答的方式来推导这个公式。
问题1:假设我们已经知道 11 个人时,幸存者的下标位置为 6,那么下一轮 10 个人时,幸存者下标的位置是多少?
答:我们在第 1 轮杀掉第 3 个人时,后面的人都往前面移动了 3 位,幸存者也往前移动了 3 位,所以他的下标由 6 变成了 3。
问题2:假设我们呢已经知道 10 个人时,幸存者的下标位置为 3,那么上一轮 11 个人时,幸存者下标的位置是多少?
答:这可以看成是上一个问题的逆过程,所以由 10 变成 11 个人时,所有人都往后移动 3 位,所以 \(J(11, 3) = J(10, 3) + 3\),不过数组可能会越界,我们可以想象成数组的首尾是相接的环,那么越界的元素就要重新回到开头,所以这个式子还要模上当前的人数(注意,这里是当前数组,在这里就是人数为 11 的这个数组):\(J(11,3) = (J(10, 3) + 3) % 11\)。
问题3:推及到一般情况,人数为 n,报到 k 时,把那个人杀掉,那么数组又是怎么移动的?
答:由上面的推导,我们应该很容易就能得出,若已知 n - 1 个人时,幸存者的下标位置为 \(J(n - 1, k)\),那么 n 个人的时候,就是往后移动 k 位,同样的,因为可能数组越界,所以式子要变成:\(J(n, k) = (J(n - 1, k) + 3) % n\)
C语言代码实现:
#include <stdio.h>
int JoseCir(int n, int k)
{
int p = 0; // 只剩一个人时,数组下标为 0
for (int i = 2; i <= n; i++)
{
p = (p + k) % i; // i 是当前的人数,即数组的规模
}
return p + 1; // 因为数组是从 0 开始,所以返回的幸存者编号需要加 1
}
int main()
{
int n = 11, k = 3;
int res;
res = JoseCir(n, k);
printf("幸存者的编号为:%d", res);
return 0;
}
测试结果:

参考:
https://blog.csdn.net/u011500062/article/details/72855826
https://blog.csdn.net/wenhai_zh/article/details/9620847





