[array] leetcode - 42. Trapping Rain Water - Hard

leetcode - 42. Trapping Rain Water - Hard

descrition

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

For example,
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

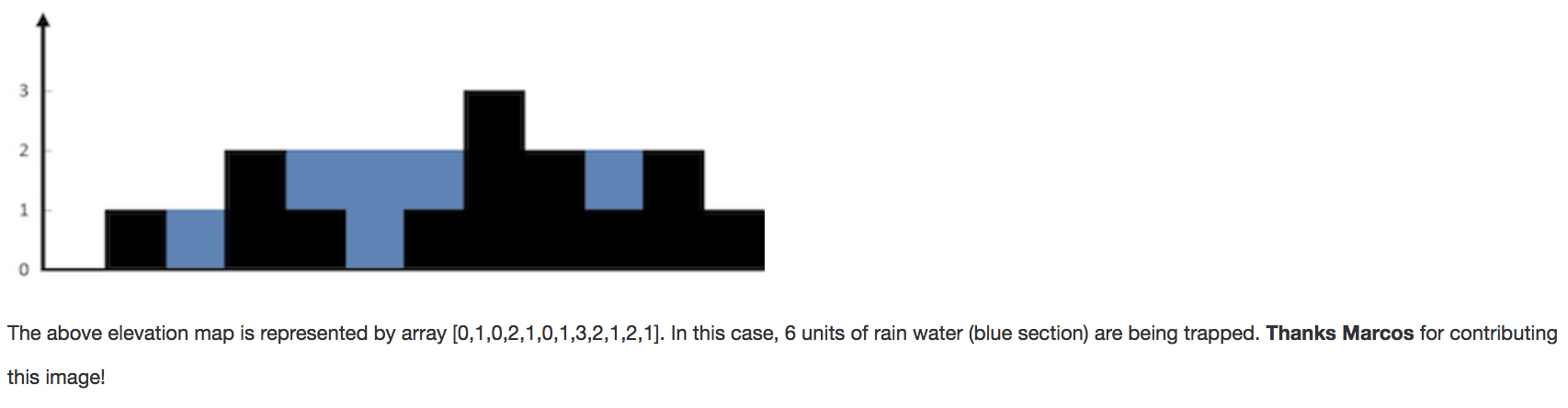
解析

关键是要想到暴力的解法，然后逐步优化。理解的过程中建议作图。

height[]，每个槽的宽度为 1。

方法-1-Brute force

对于任意两个点 i，j，height[i] 和 height[j]，并且 i != j，那么 [i,j] 区间将形成一个储水槽，储水量取决于两则高度偏小的一方。对于任意 k=(i,j) && height[k] < min(height[i], height[j])，那么位置 k 储水量应该为 water_k = min(height[i], height[j]) - height[k]， 将所有满足要求的 k 检查一遍并将储水量相加，则可得到 [i,j] 区间水槽的储水量。

根据上面的基本思路，稍微换个角度，对于任意 k = [0,n-1]，计算其储水量并累加即可得到总的储水量。对于任意位置 k 有，water_k = min(max_left, max_right) - height[k]，其中 max_left 是指 [0,..,k-1] 中最大的高度，max_right 指 [k+1,...,n-1] 中最大的高度。
其实很容易理解，对于任意位置 k，我们希望计算其储水量，需要找到包含它的水槽即可，假设水槽的高度为 height_x，那么 k 在水槽中贡献的储水量为 water_k = height_x - k，此时，若 height_x 越大，那么 water_k 将越大，也就是说 water_k 取决于最大的 height_x，因此我们要找的是包含 k 的最大的水槽，那就是其左边最大的高度 left_max 和右边最大的高度 right_max 形成的水槽。

具体实现见代码。两重循环时间复杂度为 O(n^2)，空间复杂度 O(1)。下面的 3 种方法实际上是在此基础上的改进，主要是通过某种技巧来获取 left_max, right_max 的信息，以达到降低时间复杂度的目的，最优时间复杂度可达到 O(n)

方法-2-Dynamic Programming

方法 1 中，我们计算任意位置 i 的储水量，需要知道 left_max 和 right_max。如果我们可以事先将这些信息存储起来，那么时间复杂度将可以进一步降低。

以空间换时间。假设 left_max[i] 表示 height[0,...,i] 的最大值，right_max[i] 表示height[i,...,n-1] 的最大值。我们实用动态规划的思想可以在 O(n) 时间复杂度内计算得到两个数组的信息，left_max[i] = max(height[i], left_max[i-1]), right_max[i] = max(height[i], right_max[i+1])。在此基础上我们只需要一层循环即可将储水量统计出来，对于任意位置 i，water_i = min(left_max[i], right_max[i]) - height[i]。

因此总的复杂度为 O(n)，空间复杂度为 O(n)。

方法-3-Using Stacks

我们以上计算是从 i 往两边发散，这里的着眼点是否可以是一个方向呢？

我们借助一个栈 stack 来存储当前访问过的下标，stack 所存储下标对应的高度从栈底到栈顶是呈递减有序的（可以参考代码，按照入栈和出栈的规则很容易得到此结论，可以用反证法进行证明）。

算法参考代码。逻辑解释：

假设 icurrent=[0,...n-1]，从前往后遍历，每次循环中我们都检查 stack 栈顶元素，

• 如果 stack.top > height[icurrent]，那么弹出栈顶到 itop，此时如果 stack 为空那么表明 itop 位置左边已经没有比它高的元素不能形成蓄水池，跳出内层循环；否则，由 stack 的性质可以得知，新的栈顶 stack.top 和 icurrent 可以构成蓄水池，蓄水池的宽度由 stack.top 和 icurrent 的距离决定，而高度由 itop 和 icurrent 中较小者决定。
• 当上面的循环解释后，将当前位置入栈。

此处比较核心的点在于时间复杂度的分析。不要看有两重 while 就误认为时间复杂度是 O(n^2)。从 stack 的角度分析，两重 while 循环中，每个元素只能被访问两次，一次是入栈，一次是出栈，总共有 n 个元素，因此循环执行 2n 次，时间复杂度为 O(n)。

另一个值得注意的是，蓄水量的计算方式有所不同

方法-4-Using 2 pointers

方法 2 中，注意到，对于任意位置 i

• (1)当 right_max[i] > left_max[i] 时，储水量取决于 left_max[i]，其中 left_max[i] 存储 [0,...,i] 的最大值；
• (2)当 right_max[i] < left_max[i] 时，储水量取决于 right_max[i]，其中 right_max[i] 存储 [i,...,n-1] 的最大值；

我们可以使用两个指针 left 和 right，分别从左往右，从右往左遍历数组，同时使用两个变量 left_max 和 right_max 记录左边和右边的最大值。在任意时刻，left 或 right 就相当于上面的 i，当 height[left] < height[right] 时，等价于上面的情况 （1），储水量只取决于 left_max，并且继续从左往右遍历，left++；反方向的情况类似。

可以参考官网的 solution，有配图：
leetcode-solution

code

#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>

using namespace std;

class Solution{
public:
	int trap(vector<int>& height){
		//return trap_brute_force(height);
		//return trap_dynamic_programming(height);
		//return trap_stack(height);
		return trap_two_pointer(height);
	}

	// time-O(n^2), space-O(1)
	int trap_brute_force(vector<int>& height){
		int ans = 0;
		for(int i=0; i<height.size(); ++i){
			int left_max = 0, right_max = 0;
			for(int j=i; j>=0; --j)
				left_max = max(left_max, height[j]);
			for(int j=i; j<height.size(); ++j)
				right_max = max(right_max, height[j]);

			ans += min(left_max, right_max) - height[i]; 
		}

		return ans;
	}

	// time-O(n), space-O(n)
	int trap_dynamic_programming(vector<int>& height){
		if(height.empty())
			return 0;

		int n = height.size();
		vector<int> left_max(n, 0);
		vector<int> right_max(n, 0);
		int ans = 0;

		// calcualte left and right max with dynamic programming
		left_max[0] = height[0]; // Note: height can not be empty!
		for(int i=1; i<n; ++i)
			left_max[i] = max(height[i], left_max[i-1]);
		right_max[n-1] = height[n-1];
		for(int i=n-2; i>=0; --i)
			right_max[i] = max(height[i], right_max[i+1]);

		// calculate trapped water
		for(int i=0; i<n; i++){
			ans += min(left_max[i], right_max[i]) - height[i];
		}

		return ans;
	}

	// time-O(n), for each element in height[], they are just visited twice, 
	// push into stack and pop from the stack.
	// space-O(n)
	int trap_stack(vector<int>& height){
		stack<int> st;
		int ans = 0;
		int icur = 0;

		// st is in descending from bottom to top if it work with the following rule
		while(icur < height.size()){
			while(!st.empty() && height[st.top()] < height[icur]){
				int itop = st.top();
				st.pop();
				if(st.empty())
					break;
				int width = icur - st.top() - 1;
				int bounded_height = min(height[icur], height[st.top()]) - height[itop];
				ans += width * bounded_height;
			}
			st.push(icur);
			icur++;
		}

		return ans;
	}

	// time-O(n), space-O(1)
	int trap_two_pointer(vector<int>& height){
		int left = 0;
		int right = height.size() - 1;
		int left_max = 0; // the max hight in range [0, ..., left-1]
		int right_max = 0; // the max hight in range [right+1, ..., n-1]
		int ans = 0;
		while(left < right){
			if(height[left] < height[right]){
				// the water trapped would be dependant on height of bar in current 
				// direction (from left to right)
				height[left] >= left_max ? (left_max = height[left]) 
				                         : ans += (left_max - height[left]);
				left++;
			}else{
				//height[left] >= height[right]
				// the water trapped would be dependant on height of bar in current 
				// direction (from right to left)
				height[right] >= right_max ? (right_max = height[right]) 
				                            : ans += (right_max - height[right]);
				right--;
			}
		}
		return ans;
	}
};

int main()
{
	return 0;
}