P5663 加工零件
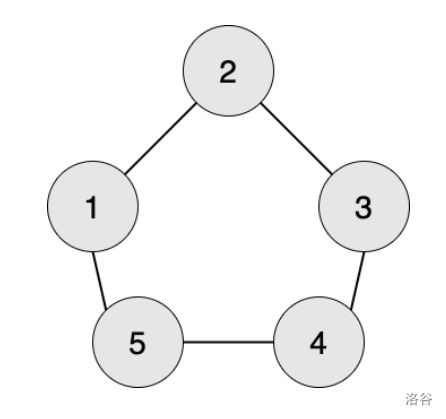
设求第3点为第3阶段时,点1是否需要提供原材料。
【3,3】 => 【2,2】,【4,2】
【2,2】 => 【1,1】,【3,1】
【4,2】 => 【3,1】,【5,1】
【1,1】 => 【2,0】,【5,0】
【3,1】 => 【2,0】,【4,0】
【5,1】 => 【1,0】,【4,0】 # 此处1需要提供原材料
比较容易想到对于每个询问进行暴搜,若点1为0,则Yes
时间复杂度很高,必然超时。
40-60分算法
#include <bits/stdc++.h> using namespace std; const int MAXN=1005; int vex[MAXN],k,n,m,q; struct edge { int u,v,next; }e[MAXN*2]; int vis[MAXN][MAXN]; void add(int u,int v){ k++; e[k].u=u; e[k].v=v; e[k].next=vex[u]; vex[u]=k; } void dfs(int u,int s){ if(s==-1||vis[u][s]) return; vis[u][s]=1; for(int i=vex[u];i;i=e[i].next){ int v=e[i].v; dfs(v,s-1); } return; } int main(){ cin>>n>>m>>q; while(m--){ int u,v; cin>>u>>v; add(u,v); add(v,u); } while(q--){ int u,L; memset(vis,0,sizeof(vis)); cin>>u>>L; dfs(u,L); if(vis[1][0]) cout<<"Yes"<<endl; else cout<<"No"<<endl; } return 0; }
满分算法
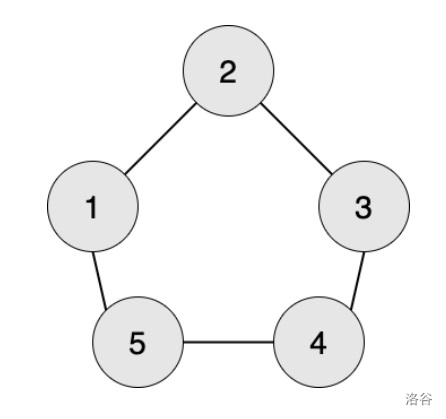
观察发现,由于1->2的路径长度为1,只要点2的阶段为奇数,则点1一定要提供原材料(1->2->1->2->...)
观察发现,由于1->2->3的路径长度为2,只要点3的阶段为偶数,则点1一定要提供原材料
从1到v,路径很多,长度不尽相同。如果1到v的路径长度存在4时,v在阶段4、6、8、10…时,1肯定可以为0。当v的路径长度存在3时,v在3、5、7、9…阶段,1肯定可以为0。
因此要求的就是1到v的最短奇数路径和最短偶数路径。
若v的阶段为偶数x,存在v的最短偶数路径y,满足x>=y,1即可为0。
若v的阶段为奇数x,存在v的最短奇数路径y,满足x>=y,1即可为0。
设dis[v][0]为1到v的最短偶数路径,设dis[v][1]为1到v的最短奇数路径,
则有:
dis[v][0] = min(dis[v][0],dis[u][1]+1)
dis[v][1] = min(dis[v][1],dis[u][0]+1)
对于初始点1,dis[1][0]显然等于0,dis[1][1]显然不可能,设为无穷大。
#include <bits/stdc++.h> using namespace std; const int MAXN=1e5+5; int vex[MAXN],k,n,m,q; struct edge { int u,v,next; } e[MAXN*2]; int vis[MAXN][2],dis[MAXN][2],que[MAXN*10],q2[MAXN*10],head,rear; void add(int u,int v) { k++; e[k].u=u; e[k].v=v; e[k].next=vex[u]; vex[u]=k; } void SPFA() { for(int i=1; i<=n; i++) dis[i][0]=dis[i][1]=1e9; dis[1][0]=0; head=1; rear=0; que[++rear]=1; while(head<=rear) { int u=que[head]; int t=q2[head]; head++; vis[u][t]=0; for(int i=vex[u]; i; i=e[i].next) { int v=e[i].v; if(dis[v][0]>dis[u][1]+1) { dis[v][0]=dis[u][1]+1; if(!vis[v][0]) { vis[v][0]=1; que[++rear]=v; q2[rear]=0; } } if(dis[v][1]>dis[u][0]+1) { dis[v][1]=dis[u][0]+1; if(!vis[v][1]) { vis[v][1]=1; que[++rear]=v; q2[rear]=1; } } } } return; } int main() { freopen("work.in","r",stdin); freopen("work.out","w",stdout); cin>>n>>m>>q; while(m--) { int u,v; cin>>u>>v; add(u,v); add(v,u); } SPFA(); if(vex[1]==0) dis[1][0]=1e9; //补丁,若1点没有连接边,则1的偶数路径没有。 while(q--) { int u,L; cin>>u>>L; if(L>=dis[u][L%2]) cout<<"Yes"<<endl; else cout<<"No"<<endl; } return 0; }


