【模板】LCA(tarjan)
1 #include<iostream> 2 #include<vector> 3 using namespace std; 4 const int N = 10010; 5 vector<int>tree[N]; 6 vector<int>que[N]; 7 int par[N]; 8 int anc[N]; 9 int in[N]; 10 bool visited[N]; 11 12 int getpar(int x){ 13 if(par[x] != x) 14 par[x] = getpar(par[x]); 15 return par[x]; 16 } 17 void merge(int x, int y){ 18 int fx = getpar(x); 19 int fy = getpar(y); 20 if(fx == fy) return; 21 else 22 par[fx] = fy; 23 } 24 void tarjan(int x){ 25 for(int i = 0; i < tree[x].size(); i++){ 26 tarjan(tree[x][i]); 27 merge(tree[x][i], x); 28 anc[getpar(x)] = x; 29 } 30 visited[x] = true; 31 for(int i = 0; i < que[x].size(); i++){ 32 if(visited[que[x][i]]) 33 cout<<x<<" "<<que[x][i]<<" "<<anc[getpar(que[x][i])]<<endl; 34 } 35 } 36 int main(){ 37 int n, i; 38 cin>>n; 39 for(i = 1; i < n; i++){ 40 int x, y; 41 cin>>x>>y; 42 tree[x].push_back(y); 43 in[y]++; 44 } 45 int root; 46 for(i = 1; i <= n; i++){ 47 par[i] = i; 48 anc[i] = i; 49 if(in[i]==0){ 50 root = i; 51 break; 52 } 53 } 54 int m; 55 cin>>m; 56 for(i = 1; i <= m; i++){ 57 int x, y; 58 cin>>x>>y; 59 que[x].push_back(y); 60 que[y].push_back(x); 61 } 62 tarjan(root); 63 return 0; 64 }
备注:
终于搞明白了tarjan找LCA~撒花!
以上是我“自认为美的代码”,完全按自己的代码风格写的,感觉比网上的代码都要简洁清楚哈哈哈。
看了好多资料,很多都写得很不清楚啊,代码也乱七八糟的。http://www.mamicode.com/info-detail-1067269.html的描述颇为详细,也是让我思路清晰起来的一篇。
tarjan找lca是离线的,所谓离线查询,就是指必须事先读入要查询的所有点对,因为遍历的过程就要进行查询。
这个算法,精髓在于,利用了dfs的访问顺序。当遍历完一棵子树时,回溯到这棵子树的根节点,把这棵子树合并为一个集合(并查集实现),也就是说子树的根节点就是当前节点。然后进行查询,如果此时要查询的另一个节点,如果已经访问过,那么它的祖先(anc)就是它们俩的lca。这就是最近的。
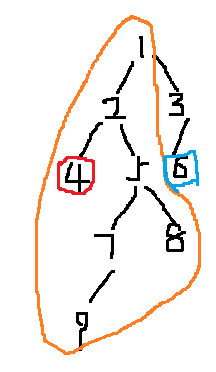
补充:比如说这幅我亲手绘的图。。虽然比较丑
当前访问完的点是6,即x为6。这时假如6还有子结点,那它们现在都合并在了6上,虽然这跟我们即将要进行的查询毫无关系。
假设我们要查询的点是4(求4和6的lca),为啥我们搜完4的时候没求出来呢,因为那会儿6还没有访问到。但现在情况就不一样了,4已经访问过了,并且现在右边橘黄色的大圈是一个大子树,4的祖先是1,而6是从1走到的,所以4和6的lca就是1.
所以,我刚才没理解的点就是,合并操作和当前要查询的点和partner没有关系,而在查询它的parner和它时才派上用场。虽然看表述只是交换了一下位置。。但其实“交换律”也是离线查询的精髓所在。。
复杂度是O(m+n),及查询数加节点数。
不要忘了初始化par和anc数组。
还有就是注意一下输入都是有向边。tarjan是从一个入度为1,即整棵树根节点开始。



