e到底是什么?
e到底是什么?
今天看到一个下面这么一个简单的求极限问题-

一时恍惚了,为什么结果是e^m。 这个e是什么呢?
然后就百度了下,发现不少文章介绍这个e.
有几篇写得很赞 -
下面摘录下第一篇文章中的部分内容,通过复利的方式来介绍e -
Money Changes Everything
But money is different. As soon as we earn a penny of interest, that penny can start earning micro-pennies of its own. We don’t need to wait until we earn a complete dollar in interest — fresh money doesn’t need to mature.
Based on our old formula, interest growth looks like this:
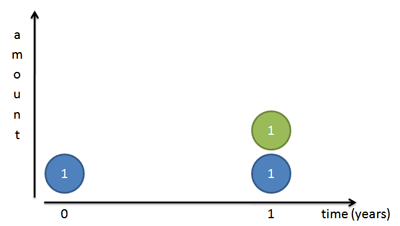
But again, this isn’t quite right: all the interest appears on the last day. Let’s zoom in and split the year into two chunks. We earn 100% interest every year, or 50% every 6 months. So, we earn 50 cents the first 6 months and another 50 cents in the last half of the year:
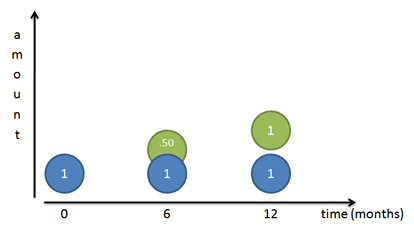
But this still isn’t right! Sure, our original dollar (Mr. Blue) earns a dollar over the course of a year. But after 6 months we had a 50-cent piece, ready to go, that we neglected! That 50 cents could have earned money on its own:
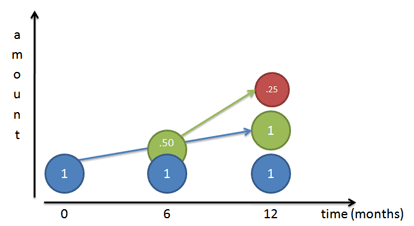
Because our rate is 50% per half year, that 50 cents would have earned 25 cents (50% times 50 cents). At the end of 1 year we’d have
- Our original dollar (Mr. Blue)
- The dollar Mr. Blue made (Mr. Green)
- The 25 cents Mr. Green made (Mr. Red)
Giving us a total of $2.25. We gained $1.25 from our initial dollar, even better than doubling!
Let’s turn our return into a formula. The growth of two half-periods of 50% is:
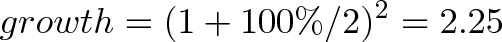
Diving into Compound Growth
It’s time to step it up a notch. Instead of splitting growth into two periods of 50% increase, let’s split it into 3 segments of 33% growth. Who says we have to wait for 6 months before we start getting interest? Let’s get more granular in our counting.
Charting our growth for 3 compounded periods gives a funny picture:
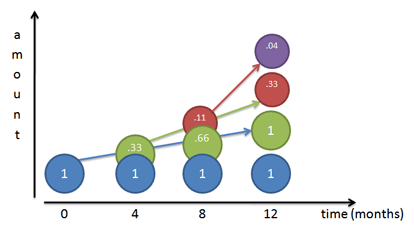
Think of each color as shoveling money upwards towards the other colors (its children), at 33% per period:
Month 0: We start with Mr. Blue at $1.
Month 4: Mr. Blue has earned 1/3 dollar on himself, and creates Mr. Green, shoveling along 33 cents.
Month 8: Mr. Blue earns another 33 cents and gives it to Mr. Green, bringing Mr. Green up to 66 cents. Mr. Green has actually earned 33% on his previous value, creating 11 cents (33% * 33 cents). This 11 cents becomes Mr. Red.
Month 12: Things get a bit crazy. Mr. Blue earns another 33 cents and shovels it to Mr. Green, bringing Mr. Green to a full dollar. Mr. Green earns 33% return on his Month 8 value (66 cents), earning 22 cents. This 22 cents gets added to Mr. Red, who now totals 33 cents. And Mr. Red, who started at 11 cents, has earned 4 cents (33% * .11) on his own, creating Mr. Purple.
Phew! The final value after 12 months is: 1 + 1 + .33 + .04 or about 2.37.
Take some time to really understand what’s happening with this growth:
- Each color earns interest on itself and hands it off to another color. The newly-created money can earn money of its own, and on the cycle goes.
- I like to think of the original amount (Mr. Blue) as never changing. Mr. Blue shovels money to create Mr. Green, a steady 33 every 4 months since Mr. Blue does not change. In the diagram, Mr. Blue has a blue arrow showing how he feeds Mr. Green.
- Mr. Green just happens to create and feed Mr. Red (green arrow), but Mr. Blue isn’t aware of this.
- As Mr. Green grows over time (being constantly fed by Mr. Blue), he contributes more and more to Mr. Red. Between months 4-8 Mr. Green gives 11 cents to Mr. Red. Between months 8-12 Mr. Green gives 22 cents to Mr. Red, since Mr. Green was at 66 cents during Month 8. If we expanded the chart, Mr. Green would give 33 cents to Mr. Red, since Mr. Green reached a full dollar by Month 12.
Make sense? It’s tough at first — I even confused myself a bit while putting the charts together. But see that each dollar creates little helpers, who in turn create helpers, and so on.
We get a formula by using 3 periods in our growth equation:
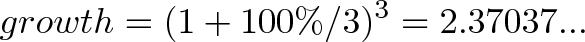
We earned $1.37, even better than the $1.25 we got last time!
Can We Get Infinite Money?
Why not take even shorter time periods? How about every month, day, hour, or even nanosecond? Will our returns skyrocket?
Our return gets better, but only to a point. Try using different numbers of n in our magic formula to see our total return:
- n (1 + 1/n)^n
- 1 2
- 2 2.25
- 3 2.37
- 5 2.488
- 10 2.5937
- 100 2.7048
- 1,000 2.7169
- 10,000 2.71814
- 100,000 2.718268
- 1,000,000 2.7182804
...
The numbers get bigger and converge around 2.718. Hey… wait a minute… that looks like e!
Yowza. In geeky math terms, e is defined to be that rate of growth if we continually compound 100% return on smaller and smaller time periods:
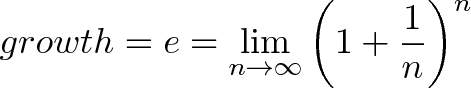
This limit appears to converge, and there are proofs to that effect. But as you can see, as we take finer time periods the total return stays around 2.718.
But what does it all mean?
The number e (2.718…) is the maximum possible result when compounding 100% growth for one time period. Sure, you started out expecting to grow from 1 to 2 (that’s a 100% increase, right?). But with each tiny step forward you create a little dividend that starts growing on its own. When all is said and done, you end up with e (2.718…) at the end of 1 time period, not 2. e is the maximum, what happens when we compound 100% as much as possible.
So, if we start with $1.00 and compound continuously at 100% return we get 1e. If we start with $2.00, we get 2e. If we start with $11.79, we get 11.79e.
e is like a speed limit (like c, the speed of light) saying how fast you can possibly grow using a continuous process. You might not always reach the speed limit, but it’s a reference point: you can write every rate of growth in terms of this universal constant.
(Aside: Be careful about separating the increase from the final result. 1 becoming e (2.718…) is an increase (growth rate) of 171.8%. e, by itself, is the final result you observe after all growth is taken into account (original + increase)).
What about different rates?
Good question. What if we grow at 50% annually, instead of 100%? Can we still use e?
Let’s see. The rate of 50% compound growth would look like this:
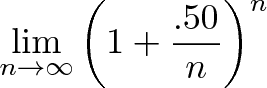
Hrm. What can we do here? Remember, 50% is the total return, and n is the number of periods to split the growth into for compounding. If we pick n=50, we can split our growth into 50 chunks of 1% interest:
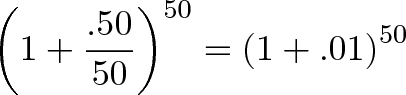
Sure, it’s not infinity, but it’s pretty granular. Now imagine we also divided our regular rate of 100% into chunks of 1%:
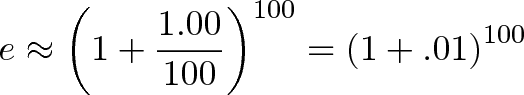
Ah, something is emerging here. In our regular case, we have 100 cumulative changes of 1% each. In the 50% scenario, we have 50 cumulative changes of 1% each.
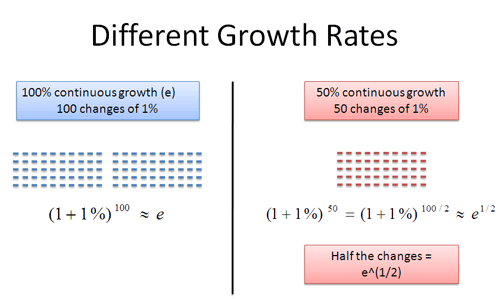
What is the difference between the two numbers? Well, it’s just half the number of changes:
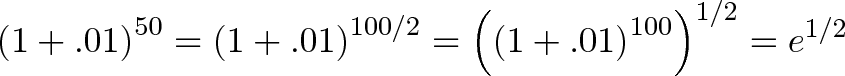
This is pretty interesting. 50 / 100 = .5, which is the exponent we raise e to. This works in general: if we had a 300% growth rate, we could break it into 300 chunks of 1% growth. This would be triple the normal amount for a net rate of e3.
Even though growth can look like addition (+1%), we need to remember that it’s really a multiplication (x 1.01). This is why we use exponents (repeated multiplication) and square roots (e1/2 means “half” the number of changes, i.e. half the number of multiplications).
Although we picked 1%, we could have chosen any small unit of growth (.1%, .0001%, or even an infinitely small amount!). The key is that for any rate we pick, it’s just a new exponent on e:
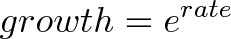
What about different times?
Suppose we have 300% growth for 2 years. We’d multiply one year’s growth (e3) by itself:
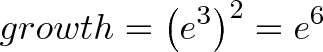
And in general:
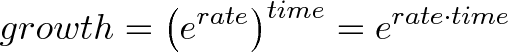
Because of the magic of exponents, we can avoid having two powers and just multiply rate and time together in a single exponent.
--------------------------------------
Regards,
FangwenYu



