描述
给定一个字符串s,找到其中最长的回文子序列。可以假设s的最大长度为1000。
示例 1:
输入:
"bbbab"
输出:
4
一个可能的最长回文子序列为 "bbbb"。
示例 2:
输入:
"cbbd"
输出:
2
一个可能的最长回文子序列为 "bb"。
解析
基本思路
我们说这个问题对 dp 数组的定义是:在子串 s[i..j] 中,最长回文子序列的长度为 dp[i][j]。一定要记住这个定义才能理解算法。
为啥这个问题要这样定义二维的 dp 数组呢?我们前文多次提到,找状态转移需要归纳思维,说白了就是如何从已知的结果推出未知的部分,这样定义容易归纳,容易发现状态转移关系。
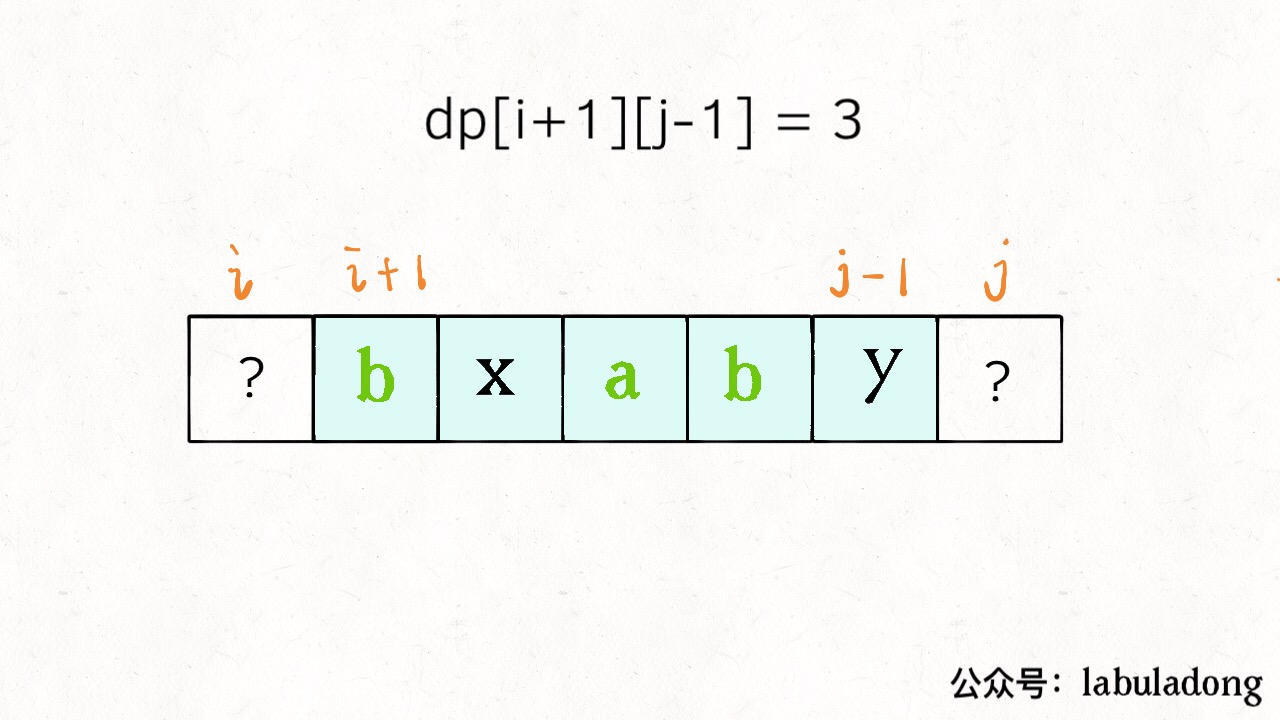
具体来说,如果我们想求 dp[i][j],假设你知道了子问题 dp[i+1][j-1] 的结果(s[i+1..j-1] 中最长回文子序列的长度),你是否能想办法算出 dp[i][j] 的值(s[i..j] 中,最长回文子序列的长度)呢?
可以!这取决于 s[i] 和 s[j] 的字符:
如果它俩相等,那么它俩加上 s[i+1..j-1] 中的最长回文子序列就是 s[i..j] 的最长回文子序列:

如果它俩不相等,说明它俩不可能同时出现在 s[i..j] 的最长回文子序列中,那么把它俩分别加入 s[i+1..j-1] 中,看看哪个子串产生的回文子序列更长即可:
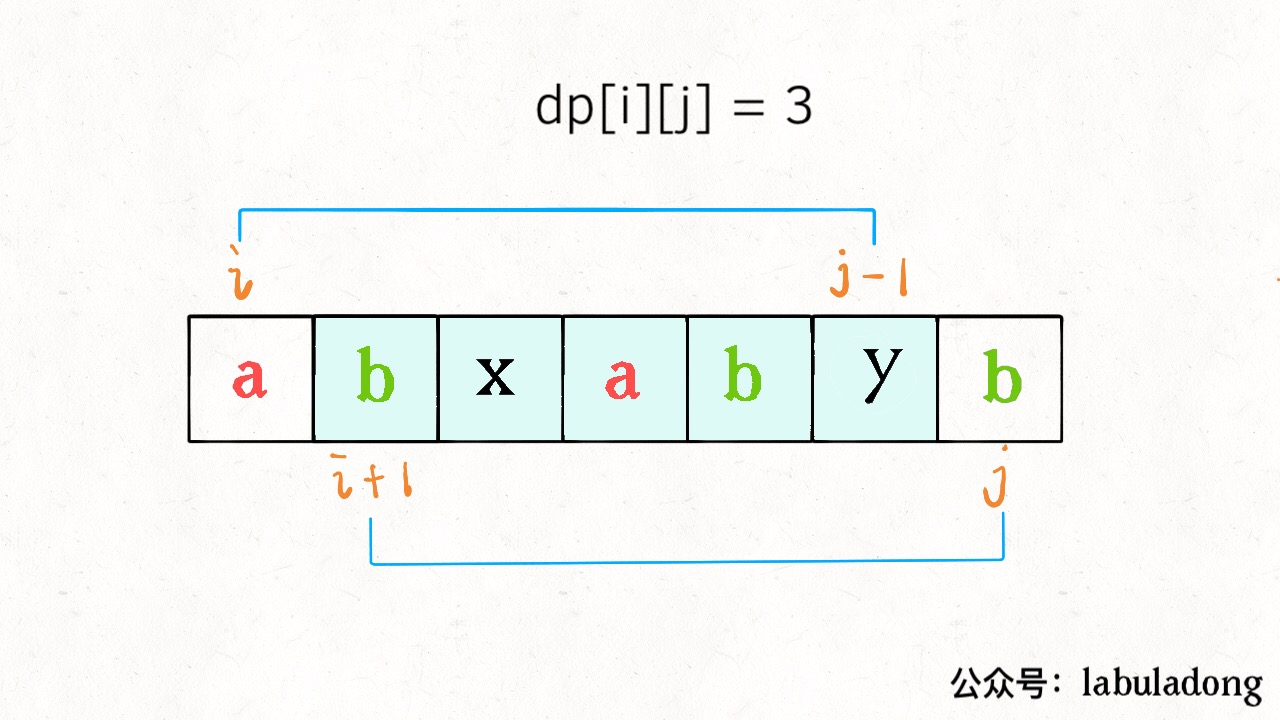
以上两种情况写成代码就是这样:
if (s[i] == s[j]) // 它俩一定在最长回文子序列中 dp[i][j] = dp[i + 1][j - 1] + 2; else // s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长? dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
至此,状态转移方程就写出来了,根据 dp 数组的定义,我们要求的就是 dp[0][n - 1],也就是整个 s 的最长回文子序列的长度。
具体实现
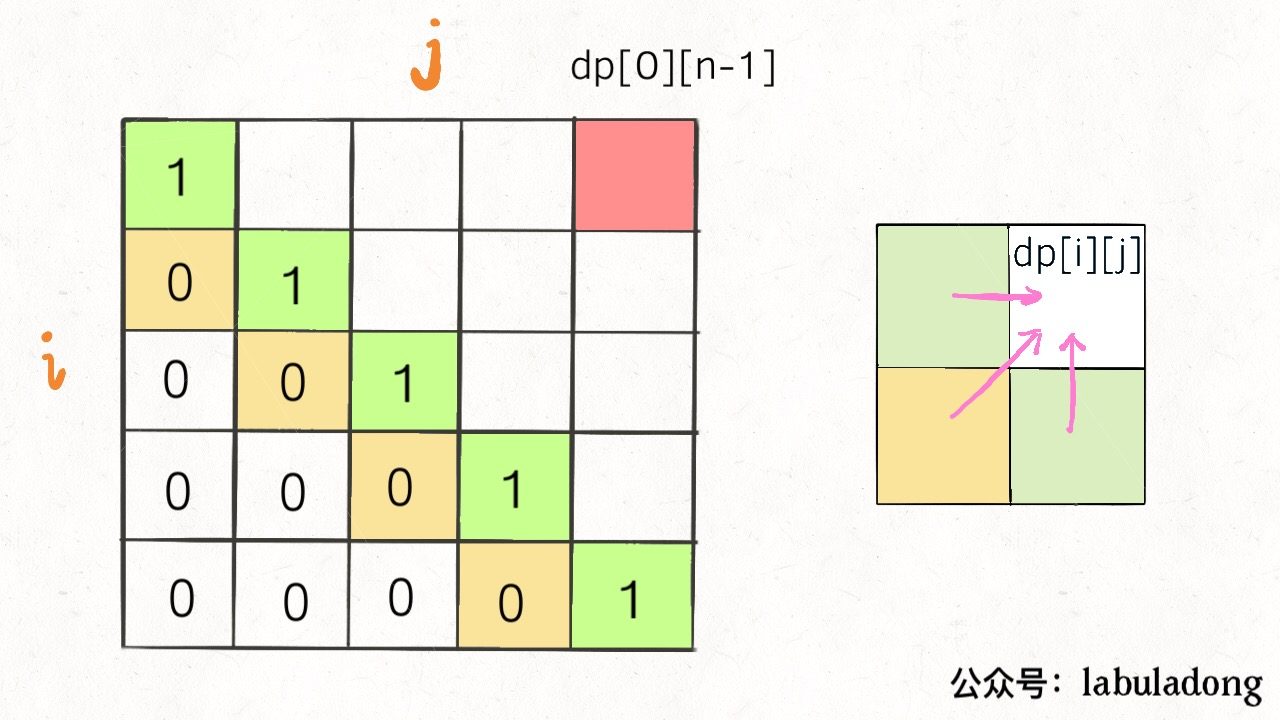
首先明确一下 base case,如果只有一个字符,显然最长回文子序列长度是 1,也就是 dp[i][j] = 1 (i == j)。
因为 i 肯定小于等于 j,所以对于那些 i > j 的位置,根本不存在什么子序列,应该初始化为 0。
另外,看看刚才写的状态转移方程,想求 dp[i][j] 需要知道 dp[i+1][j-1],dp[i+1][j],dp[i][j-1] 这三个位置;再看看我们确定的 base case,填入 dp 数组之后是这样:
为了保证每次计算 dp[i][j],左下右方向的位置已经被计算出来,只能斜着遍历或者反着遍历:
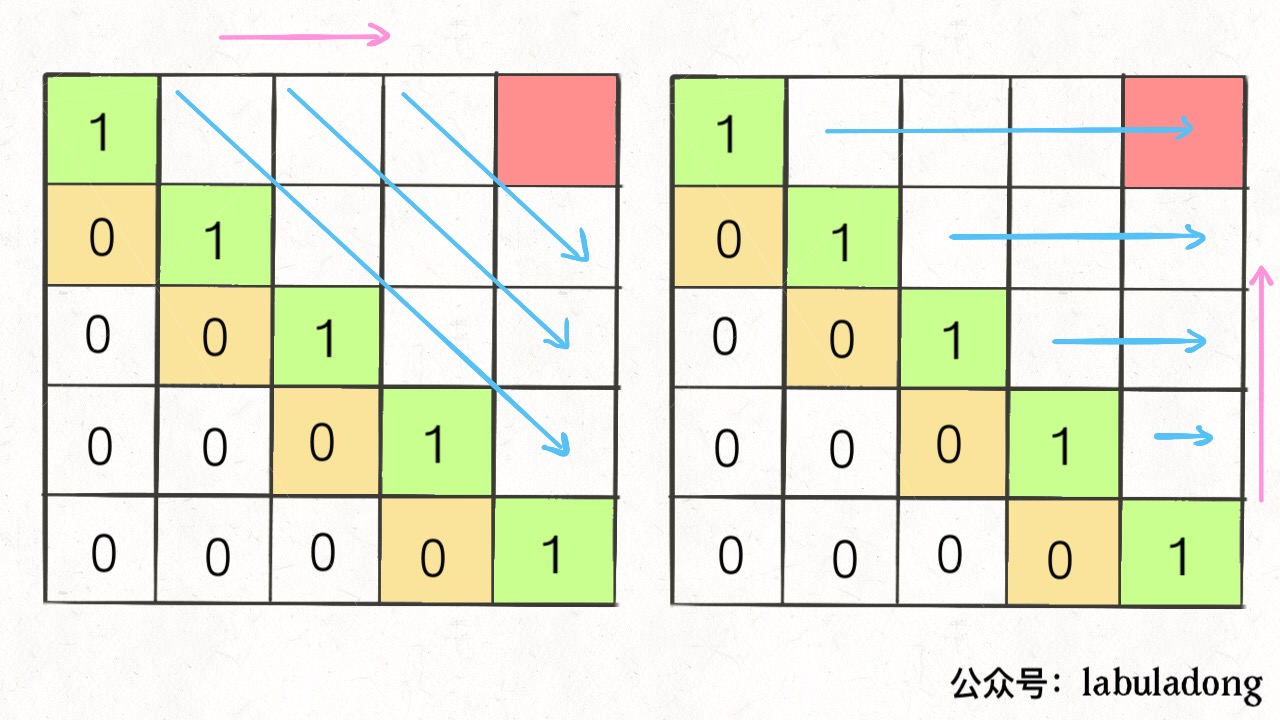
我选择反着遍历,代码如下:
代码
int longestPalindromeSubseq(String s) { int n = s.size(); // dp 数组全部初始化为 0 int[][] dp = new int[n][n];// base case for (int i = 0; i < n; i++) dp[i][i] = 1; // 反着遍历保证正确的状态转移 for (int i = n - 1; i >= 0; i--) { for (int j = i + 1; j < n; j++) { // 状态转移方程 if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1] + 2; else dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); } } // 整个 s 的最长回文子串长度 return dp[0][n - 1]; }



