描述
给你一个字符串 S、一个字符串 T,请在字符串 S 里面找出:包含 T 所有字母的最小子串。
示例:
输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"
说明:
如果 S 中不存这样的子串,则返回空字符串 ""。
如果 S 中存在这样的子串,我们保证它是唯一的答案。
解析
题目不难理解,就是说要在 S(source) 中找到包含 T(target) 中全部字母的一个子串,顺序无所谓,但这个子串一定是所有可能子串中最短的。
如果我们使用暴力解法,代码大概是这样的:
for (int i = 0; i < s.size(); i++) for (int j = i + 1; j < s.size(); j++) if s[i:j] 包含 t 的所有字母: 更新答案
思路很直接吧,但是显然,这个算法的复杂度肯定大于 O(N^2) 了,不好。
滑动窗口算法的思路是这样:
1、我们在字符串 S 中使用双指针中的左右指针技巧,初始化 left = right = 0,把索引闭区间 [left, right] 称为一个「窗口」。
2、我们先不断地增加 right 指针扩大窗口 [left, right],直到窗口中的字符串符合要求(包含了 T 中的所有字符)。
3、此时,我们停止增加 right,转而不断增加 left 指针缩小窗口 [left, right],直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同时,每次增加 left,我们都要更新一轮结果。
4、重复第 2 和第 3 步,直到 right 到达字符串 S 的尽头。
这个思路其实也不难,第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解。左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动。
下面画图理解一下,needs 和 window 相当于计数器,分别记录 T 中字符出现次数和窗口中的相应字符的出现次数。
初始状态:
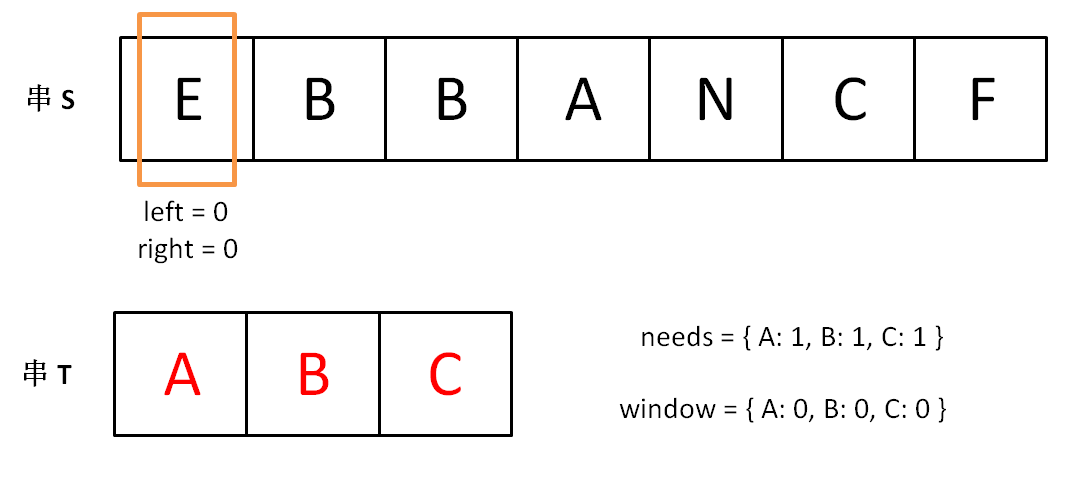
增加 right,直到窗口 [left, right] 包含了 T 中所有字符:
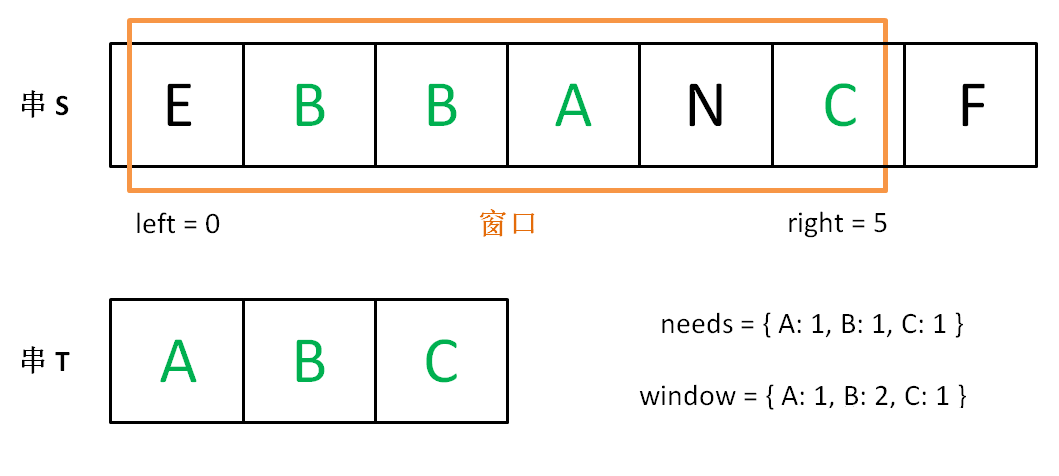
现在开始增加 left,缩小窗口 [left, right]。
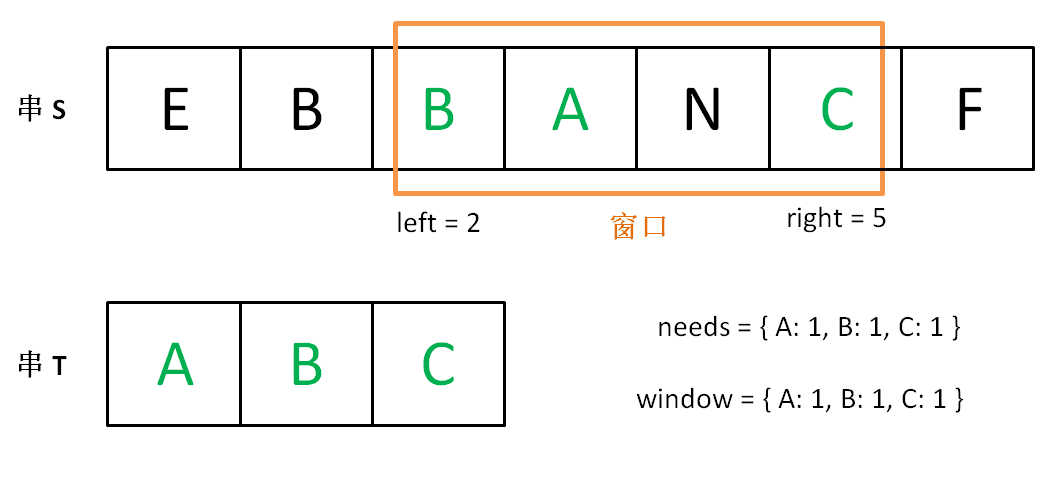
直到窗口中的字符串不再符合要求,left 不再继续移动。

之后重复上述过程,先移动 right,再移动 left…… 直到 right 指针到达字符串 S 的末端,算法结束。
如果你能够理解上述过程,恭喜,你已经完全掌握了滑动窗口算法思想。至于如何具体到问题,如何得出此题的答案,都是编程问题,等会提供一套模板,理解一下就会了。
上述过程可以简单地写出如下伪码框架:
string s, t; // 在 s 中寻找 t 的「最小覆盖子串」 int left = 0, right = 0; string res = s; while(right < s.size()) { window.add(s[right]); right++; // 如果符合要求,移动 left 缩小窗口 while (window 符合要求) { // 如果这个窗口的子串更短,则更新 res res = minLen(res, window); window.remove(s[left]); left++; } } return res;
如果上述代码你也能够理解,那么你离解题更近了一步。现在就剩下一个比较棘手的问题:如何判断 window 即子串 s[left...right] 是否符合要求,是否包含 t 的所有字符呢?
可以用两个哈希表当作计数器解决。用一个哈希表 needs 记录字符串 t 中包含的字符及出现次数,用另一个哈希表 window 记录当前「窗口」中包含的字符及出现的次数,如果 window 包含所有 needs 中的键,且这些键对应的值都大于等于 needs 中的值,那么就可以知道当前「窗口」符合要求了,可以开始移动 left 指针了。
如果直接甩给你这么一大段代码,我想你的心态是爆炸的,但是通过之前的步步跟进,你是否能够理解这个算法的内在逻辑呢?你是否能清晰看出该算法的结构呢?
这个算法的时间复杂度是 O(M + N)O(M+N),MM 和 NN 分别是字符串 SS 和 TT 的长度。因为我们先用 forfor 循环遍历了字符串 TT 来初始化 needsneeds,时间 O(N)O(N),之后的两个 whilewhile 循环最多执行 2M2M 次,时间 O(M)O(M)。
也许认为嵌套的 while 循环复杂度应该是平方级,但是你这样想,while 执行的次数就是双指针 left 和 right 走的总路程,最多是 2M 嘛。
代码
class Solution { public String minWindow(String s, String target) { if (s == null || target == null || s.length() == 0 || target.length() == 0 || target.length() > s.length()) { return ""; } Map<Character, Integer> needs = new HashMap<>(); for (char ch : target.toCharArray()) { int nums = needs.getOrDefault(ch, 0); needs.put(ch, nums + 1); } int sLength = s.length(); int tLength = target.length(); int left = 0;//左指针 int right = 0;//右指针 int resLeftRight = Integer.MAX_VALUE;//保存最小的left、right的间隔 int minLeft = 0;//保存间隔最小的符合条件的left Map<Character, Integer> windows = new HashMap<>(); while (right < sLength) { char curChar = s.charAt(right); int curNum = windows.getOrDefault(curChar, 0); windows.put(curChar, curNum + 1); right++; while (right - left >= tLength && minWindowHelp(windows, needs)) { int curLeftRight = right - left; if (curLeftRight < resLeftRight) { //可能有很多符合条件的,比较出left、right间隔最小的 minLeft = left; resLeftRight = curLeftRight; } char leftChar = s.charAt(left); int leftCharNum = windows.get(leftChar); if (leftCharNum == 1) { windows.remove(leftChar); } else { windows.put(leftChar, leftCharNum - 1); } left++; } } return resLeftRight == Integer.MAX_VALUE ? "" : s.substring(minLeft, minLeft + resLeftRight); } public boolean minWindowHelp(Map<Character, Integer> windows, Map<Character, Integer> needs) { if (windows.size() < needs.size()) { return false; } for (Map.Entry<Character, Integer> entry : needs.entrySet()) { Character key = entry.getKey(); int num = entry.getValue(); if (!windows.containsKey(key) || windows.get(key) < num) { return false; } } return true; } }


