行列有序的二维数组查找

描述

在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。

请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。 

输入描述:

array： 待查找的二维数组

target：查找的数字

输出描述:

查找到返回true，查找不到返回false

 

解析

分冶法

这种行和列分别递增的矩阵，有一个专有名词叫做杨氏矩阵，由剑桥大学数学家杨表在1900年推提出，在这个矩阵中的查找，俗称杨氏矩阵查找。
以查找数字6为例，因为矩阵的行和列都是递增的，所以整个矩阵的对角线上的数字也是递增的，故我们可以在对角线上进行二分查找，如果要找的数是6介于对角线上相邻的两个数4、10，可以排除掉左上和右下的两个矩形，而在左下和右上的两个矩形继续递归查找，如下图所示：

定位法

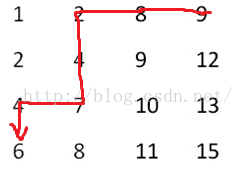
首先直接定位到最右上角的元素，再配以二分查找，比要找的数（6）大就往左走，比要找数（6）的小就往下走，直到找到要找的数字（6）为止，这个方法的时间复杂度O（m+n）。如下图所示：

代码

定位法

public class Solution {
    public boolean Find(int target, int [][] array) {
        if (null == array || array.length <= 0) {
            return false;
        }
        int row = array.length;
        int rol = array[0].length;
        int i = row - 1;
        int j = 0;
        while (i >= 0 && j < rol) {
            if (array[i][j] == target) {
                return true;
            } else if (array[i][j] > target) {
                i--;
            } else {
                j++;
            }
        }
        return false;
    }
}