题目描述
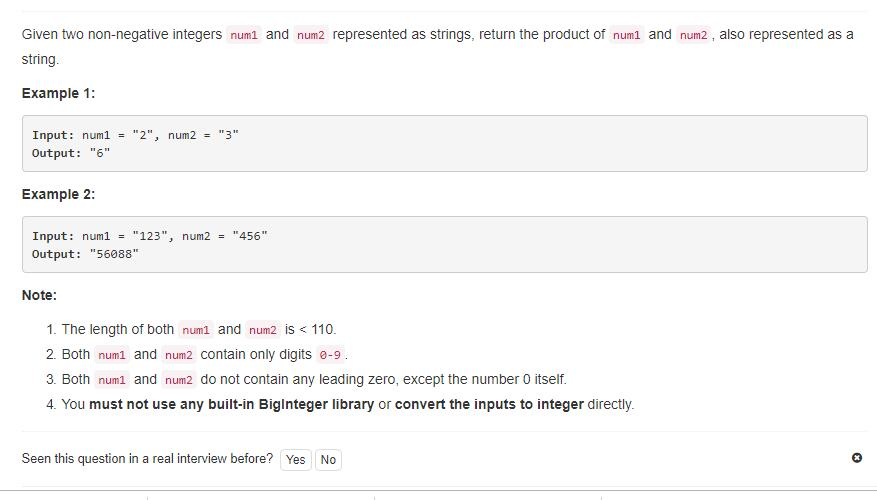
就是两个数相乘,输出结果,只不过数字很大很大,都是用 String 存储的。也就是传说中的大数相乘。
解法一
我们就模仿我们在纸上做乘法的过程写出一个算法。

个位乘个位,得出一个数,然后个位乘十位,全部乘完以后,就再用十位乘以各个位。然后百位乘以各个位,最后将每次得出的数相加。十位的结果要补 1 个 0 ,百位的结果要补两个 0 。相加的话我们可以直接用之前的大数相加。直接看代码吧。
public String multiply(String num1, String num2) { if (num1.equals("0") || num2.equals("0")) { return "0"; } String ans = "0"; int index = 0; //记录当前是哪一位,便于后边补 0 for (int i = num2.length() - 1; i >= 0; i--) { int carry = 0; //保存进位 String ans_part = ""; //直接用字符串保存每位乘出来的数 int m = num2.charAt(i) - '0'; //乘上每一位 for (int j = num1.length() - 1; j >= 0; j--) { int n = num1.charAt(j) - '0'; int mul = m * n + carry; ans_part = mul % 10 + "" + ans_part; carry = mul / 10; } if (carry > 0) { ans_part = carry + "" + ans_part; } //补 0 for (int k = 0; k < index; k++) { ans_part = ans_part + "0"; } index++; //和之前的结果相加 ans = sumString(ans, ans_part); } return ans; } //大数相加 private String sumString(String num1, String num2) { int carry = 0; int num1_index = num1.length() - 1; int num2_index = num2.length() - 1; String ans = ""; while (num1_index >= 0 || num2_index >= 0) { int n1 = num1_index >= 0 ? num1.charAt(num1_index) - '0' : 0; int n2 = num2_index >= 0 ? num2.charAt(num2_index) - '0' : 0; int sum = n1 + n2 + carry; carry = sum / 10; ans = sum % 10 + "" + ans; num1_index--; num2_index--; } if (carry > 0) { ans = carry + "" + ans; } return ans; }
时间复杂度:O(m * n)。m,n 是两个字符串的长度。
空间复杂度:O(1)。
解法二
参考这里。
上边的解法非常简单粗暴,但是不够优雅。我们看一下从未见过的一种竖式计算。
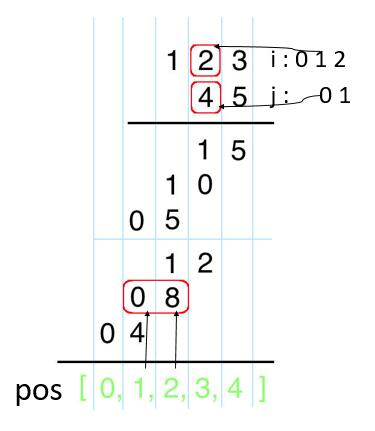
我们把进位先不算,写到对应的位置。最后再统一更新 pos 中的每一位。
而对于运算中的每个结果,可以观察出一个结论。
num1 的第 i 位乘上 num2 的第 j 位,结果会分别对应 pos 的第 i + j 位和第 i + j + 1 位。
例如图中的红色部分,num1 的第 1 位乘上 num2 的第 0 位,结果就对应 pos 的第 1 + 0 = 1 和 1 + 0 + 1 = 2 位。
有了这一点,我们就可以遍历求出每一个结果,然后更新 pos 上的值就够了。
public String multiply(String num1, String num2) { if (num1.equals("0") || num2.equals("0")) { return "0"; } int n1 = num1.length(); int n2 = num2.length(); int[] pos = new int[n1 + n2]; //保存最后的结果 for (int i = n1 - 1; i >= 0; i--) { for (int j = n2 - 1; j >= 0; j--) { //相乘的结果 int mul = (num1.charAt(i) - '0') * (num2.charAt(j) - '0'); //加上 pos[i+j+1] 之前已经累加的结果 int sum = mul + pos[i + j + 1]; //更新 pos[i + j] pos[i + j] += sum / 10; //更新 pos[i + j + 1] pos[i + j + 1] = sum % 10; } } StringBuilder sb = new StringBuilder(); for (int i = 0; i < pos.length; i++) { //判断最高位是不是 0 if (i == 0 && pos[i] == 0) { continue; } sb.append(pos[i]); } return sb.toString(); }
时间复杂度:O(m * n)。m,n 是两个字符串的长度。
空间复杂度:O(m + n)。m,n 是两个字符串的长度。
解法三(me) 完全模拟乘法进位
public String multiply(String ss, String tt) { if (null == ss || ss.length() <= 0 || null == tt || tt.length() <= 0) { return null; } if (ss.equals("0") || tt.equals("0")) { return "0"; } int ssLen = ss.length(); int ttLen = tt.length(); int[] res = new int[ssLen + ttLen];//用数组存不用long,是为了防止数字越界 int startIndex = 0;//最低位开始的index,确定是10^startIndex 的多少倍值 for (int i = ssLen - 1; i >= 0; i--) { int oldStartIndex = startIndex; int iNum = Integer.parseInt(String.valueOf(ss.charAt(i))); for (int k = ttLen - 1; k >= 0; k--) { int kNum = Integer.parseInt(String.valueOf(tt.charAt(k))); int curNum = iNum * kNum; res[startIndex] += curNum % 10; if (res[startIndex] >= 10) {//进位 res[startIndex] = res[startIndex] % 10; res[startIndex + 1] += 1; } res[startIndex + 1] += curNum / 10; if (res[startIndex + 1] >= 10) {//进位 res[startIndex + 1] = res[startIndex + 1] % 10; res[startIndex + 2] += 1; } startIndex++; } startIndex = oldStartIndex + 1; } StringBuilder sb = new StringBuilder(); boolean isStart0 = false;//去掉最高位的0 for (int i = res.length - 1; i >= 0; i--) { if (res[i] != 0 || isStart0) { sb.append(res[i]); isStart0 = true; } } return sb.toString(); }




