295. Find Median from Data Stream&数据流中的中位数
295. Find Median from Data Stream
题目
Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.
Examples:
[2,3,4] , the median is 3
[2,3], the median is (2 + 3) / 2 = 2.5
Design a data structure that supports the following two operations:
void addNum(int num) - Add a integer number from the data stream to the data structure.
double findMedian() - Return the median of all elements so far.
For example:
add(1)
add(2)
findMedian() -> 1.5
add(3)
findMedian() -> 2
题目描述
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
解析
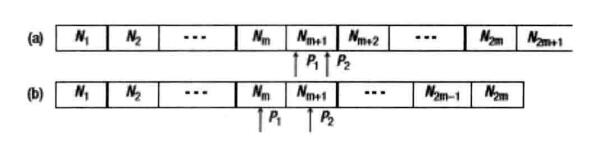
如上图所示,如果数据在容器中已经排序,那么中位数可以由P1和P2指向的数得到。如果容器中数据的个数是奇数,那么P1和P2指向同一个数据。
注意到,整个容器被分隔成了两部分。位于容器左边部分的数据比右边的数据小。另外 P1指向的是左边的最大数据, P2指向的是右边部分最小的数。
如果能够保证数据容器左边的数据都小于右边的数据,这样即使左右两边内部的数据没有排序,也可以根据左边最大的数和右边最小的数得到中位数。用最大推可以快速的从一个数据容器中找出最大数,最小堆可以快速的从一个数据容器中找出最小的数。
用一个最大堆实现左边的数据容器,用最小堆实现右边的数据容器。
首先,要保证数据平均分配到两个堆中。为了实现平均分配,可以在数据的总数目是偶数时把新数据插入到最小堆,否则插入到最大堆中。
还要保证最大堆中的数据都要小于最小堆中的数据。如果当前数据的总数目是偶数,也就是要插入最小堆,但是它比最大堆中的一些数还要小。此时,先将这个数插入到最大堆中,然后把最大堆中最大的数取出,插入到最小堆中。如果当前数据的总数目是奇数,也就是要插入最大堆,但是它比最小堆中的一些数还要大。此时,先将这个数插入到最小堆中,然后把最小堆中最小的数取出,插入到最大堆中。
代码实现
Time Complexity: addNum - O(logn) , findMedian - O(1), Space Complexity - O(n)
class MedianFinder { private PriorityQueue<Integer> maxOrientedHeap; private PriorityQueue<Integer> minOrientedHeap; public MedianFinder() { this.minOrientedHeap = new PriorityQueue<Integer>(); this.maxOrientedHeap = new PriorityQueue<Integer>(10, new Comparator<Integer>() { public int compare(Integer i1, Integer i2) { return i2 - i1; } }); } // Adds a number into the data structure. public void addNum(int num) { maxOrientedHeap.add(num); // O(logn) minOrientedHeap.add(maxOrientedHeap.poll()); // O(logn) if(maxOrientedHeap.size() < minOrientedHeap.size()) { maxOrientedHeap.add(minOrientedHeap.poll()); //O(logn) } } // Returns the median of current data stream public double findMedian() { // O(1) if(maxOrientedHeap.size() == minOrientedHeap.size()) return (maxOrientedHeap.peek() + minOrientedHeap.peek()) / 2.0; else return maxOrientedHeap.peek(); } }; // Your MedianFinder object will be instantiated and called as such: // MedianFinder mf = new MedianFinder(); // mf.addNum(1); // mf.findMedian();
class MedianFinder { Queue<Integer> minPQ = new PriorityQueue<>(); Queue<Integer> maxPQ = new PriorityQueue<>(10, (Integer i1, Integer i2) -> i2 - i1); // Adds a number into the data structure. public void addNum(int num) { minPQ.offer(num); maxPQ.offer(minPQ.poll()); if (minPQ.size() < maxPQ.size()) minPQ.offer(maxPQ.poll()); } // Returns the median of current data stream public double findMedian() { if (minPQ.size() == maxPQ.size()) return (minPQ.peek() + maxPQ.peek()) / 2.0; return minPQ.peek(); } }; // Your MedianFinder object will be instantiated and called as such: // MedianFinder mf = new MedianFinder(); // mf.addNum(1); // mf.findMedian();




