[LeetCode] 41. First Missing Positive ☆☆☆☆☆(第一个丢失的正数)

Given an unsorted integer array, find the smallest missing positive integer.

Example 1:

Input: [1,2,0]
Output: 3
Example 2:

Input: [3,4,-1,1]
Output: 2
Example 3:

Input: [7,8,9,11,12]
Output: 1
Note:

Your algorithm should run in O(n) time and uses constant extra space.

 

思路：这个题刚開始是没有思路的，难就难在O(n)时间内常数量空间，所以此题较为考察思维敏捷性。其解题核心思想是将数组的第i位存正数i+1。最后再遍历一次就可以。

其它人的思想，我也是看了这个思想自己写的代码。

 

 

尽管不能再另外开辟很数级的额外空间，可是能够在输入数组上就地进行swap操作。

思路：交换数组元素。使得数组中第i位存放数值(i+1)。

最后遍历数组，寻找第一个不符合此要求的元素，返回其下标。整个过程须要遍历两次数组，复杂度为O(n)。

下图以题目中给出的第二个样例为例，解说操作过程。

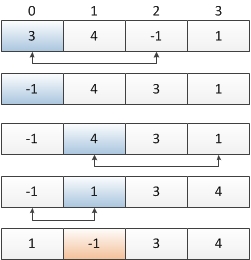
妈蛋。这题挣扎好久。

首先思路上，其次临界条件，这题和以下题异曲同工：

n个元素的数组，里面的数都是0~n-1范围内的，求数组中反复的某一个元素。没有返回-1, 要求时间性能O(n) 空间性能O(1)。

public int firstMissingPositive(int[] nums) {
        if (null == nums || nums.length == 0) {
            return 1;
        }
        for (int i = 0; i < nums.length; i++) {
            while (nums[i] > 0 && nums[i] != i + 1 && nums[i] <= nums.length) {
                int temp = nums[nums[i] - 1];
                nums[nums[i] - 1] = nums[i];
                nums[i] = temp;
            }
        }
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != i + 1) {
                return i + 1;
            }
        }
        return nums.length + 1;
    }

 

 

https://www.cnblogs.com/clnchanpin/p/6727065.html