GPS轨迹压缩之Douglas-Peucker算法
算法1
最近在做的IOT平台涉及到画轨迹线的业务。谈到轨迹线，设备上报上来的数据量巨大，甚至活跃的设备一天上报来的数据都甚至几十万。前端没法对这个数据去处理进行画线取轨迹图像。所以就有了轨迹压缩。
轨迹压缩算法
轨迹压缩算法分为两大类，分别是无损压缩和有损压缩，无损压缩算法主要包括哈夫曼编码，有损压缩算法又分为批处理方式和在线数据压缩方式，其中批处理方式又包括DP（Douglas-Peucker）算法、TD-TR（Top-Down Time-Ratio）算法和Bellman算法，在线数据压缩方式又包括滑动窗口、开放窗口、基于安全区域的方法等。
本次轨迹压缩决定采用相对简单的DP算法。
DP算法步骤如下：
（1）在轨迹曲线在曲线首尾两点A，B之间连接一条直线AB，该直线为曲线的弦；
（2）遍历曲线上其他所有点，求每个点到直线AB的距离，找到最大距离的点C，最大距离记为dmax；
（3）比较该距离dmax与预先定义的阈值Dmax大小，如果dmax<Dmax，则将该直线AB作为曲线段的近似，曲线段处理完毕；
（4）若dmax>=Dmax，则使C点将曲线AB分为AC和CB两段，并分别对这两段进行（1）~（3）步处理；
（5）当所有曲线都处理完毕时，依次连接各个分割点形成的折线，即为原始曲线的路径。
海伦公式
DP算法中需要求点到直线的距离，该距离指的是垂直欧式距离，即直线AB外的点C到直线AB的距离d，此处A、B、C三点均为经纬度坐标；我们采用三角形面积相等法求距离d，具体方法是：A、B、C三点构成三角形，该三角形的面积有两种求法，分别是普通方法（底x高/2）和海伦公式，海伦公式如下：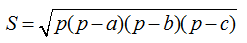
，其中p为半周长：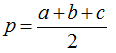
假设有一个三角形，边长分别为a、b、c，三角形的面积S可由以下公式求得：
我们通过海伦公式求得三角形面积，然后就可以求得高的大小，此处高即为距离d。要想用海伦公式，必须求出A、B、C三点两两之间的距离，该距离公式也是一个数学公式。
注意：求出距离后，要加上绝对值，以防止距离为负数。
平均误差
平均误差指的是压缩时忽略的那些点到对应线段的距离之和除以总点数得到的数值。
压缩率
压缩率的计算公式如下：
具体代码实现
1.为了DP算法压缩之后能匹配到本身数据库查询出的结果记录，（因为结果记录列表的每一条字段是可伸缩的KV对且不固定）准备一个点的实体。
@Data @NoArgsConstructor @AllArgsConstructor @ToString public class TYPoint { public String id;//点ID public double lng;//经度 public double lat;//纬度 }
2.DP算法实现类
public class DPUtil { /** * 默认的点到轨迹线最大距离误差阈值（单位：米） */ private static double defaultDMax = 30.0; /** * DP算法入口 * 传入压缩前的轨迹点集合 * 输出压缩后的结果轨迹点集合 * @param originPoints 压缩前的轨迹点集合 * @param dMax 点到轨迹线最大距离误差阈值 * @return */ public static List<TYPoint> dpAlgorithm(List<TYPoint> originPoints, Double dMax){ List<TYPoint> resultPoints = new ArrayList<>(); resultPoints.add(originPoints.get(0));//获取第一个原始经纬度点坐标并添加到过滤后的数组中 resultPoints.add(originPoints.get(originPoints.size()-1));//获取最后一个原始经纬度点坐标并添加到过滤后的数组中 //最大距离误差阈值 if(dMax == null){ dMax = defaultDMax; } int start = 0; int end = originPoints.size()-1; compression(originPoints,resultPoints,start,end,dMax); return resultPoints; } /** * 函数功能：根据最大距离限制，采用DP方法递归的对原始轨迹进行采样，得到压缩后的轨迹 * @param originPoints：原始经纬度坐标点数组 * @param resultPoints：保持过滤后的点坐标数组 * @param start：起始下标 * @param end：终点下标 * @param dMax：预先指定好的最大距离误差 计算 */ public static void compression(List<TYPoint> originPoints, List<TYPoint> resultPoints, int start, int end, double dMax){ if(start < end){//递归进行的条件 double maxDist = 0;//最大距离 int cur_pt = 0;//当前下标 for(int i=start+1;i<end;i++){ //当前点到对应线段的距离 double curDist = distToSegment(originPoints.get(start),originPoints.get(end),originPoints.get(i)); if(curDist > maxDist){ maxDist = curDist; cur_pt = i; }//求出最大距离及最大距离对应点的下标 } //若当前最大距离大于最大距离误差 if(maxDist >= dMax){ resultPoints.add(originPoints.get(cur_pt));//将当前点加入到过滤数组中 //将原来的线段以当前点为中心拆成两段，分别进行递归处理 compression(originPoints,resultPoints,start,cur_pt,dMax); compression(originPoints,resultPoints,cur_pt,end,dMax); } } } /** * 函数功能：使用三角形面积（使用海伦公式求得）相等方法计算点pX到点pA和pB所确定的直线的距离 * @param pA：起始点 * @param pB：结束点 * @param pX：第三个点 * @return distance：点pX到pA和pB所在直线的距离 */ public static double distToSegment(TYPoint pA,TYPoint pB,TYPoint pX){ double a = Math.abs(geoDist(pA, pB)); double b = Math.abs(geoDist(pA, pX)); double c = Math.abs(geoDist(pB, pX)); double p = (a+b+c)/2.0; double s = Math.sqrt(Math.abs(p*(p-a)*(p-b)*(p-c))); double d = s*2.0/a; return d; } /** * 函数功能：根据数学公式求两个经纬度点之间的距离 * @param pA：起始点 * @param pB：结束点 * @return distance：距离 */ public static double geoDist(TYPoint pA,TYPoint pB){ double radLat1 = Rad(pA.lat); double radLat2 = Rad(pB.lat); double delta_lon = Rad(pB.lng - pA.lng); double top_1 = Math.cos(radLat2) * Math.sin(delta_lon); double top_2 = Math.cos(radLat1) * Math.sin(radLat2) - Math.sin(radLat1) * Math.cos(radLat2) * Math.cos(delta_lon); double top = Math.sqrt(top_1 * top_1 + top_2 * top_2); double bottom = Math.sin(radLat1) * Math.sin(radLat2) + Math.cos(radLat1) * Math.cos(radLat2) * Math.cos(delta_lon); double delta_sigma = Math.atan2(top, bottom); double distance = delta_sigma * 6378137.0; return distance; } /** * 函数功能：角度转弧度 * @param d：角度 * @return 返回的是弧度 */ public static double Rad(double d){ return d * Math.PI / 180.0; } }
从入口代码可知dMax是可以传进来的，也就是点到轨迹直线的偏移量阈值是可以设置的。这里我设置默认dMax为30.0测试了一下，4135条数据查询出来有500条，当设置dMax为100时查询出只有289条记录了。具体看业务方需要以多大的压缩限度去压缩。
——————————————————————————————————————————————————
算法2
Douglas-Peuker正是一个对坐标关键点进行抽取的算法。算法原理
dmax，看距离是否小于给定的阈值max（及轨迹精确度）。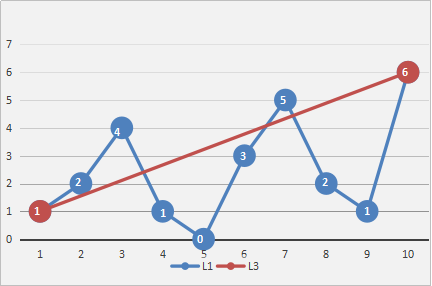
2. a.若dmax < max，则舍弃这条曲线上的所有中间点，将曲线首尾点连成的直线作为这段曲线的近似，这条线段便处理完毕。b.若dmax >= max，则以dmax所在点作为分割点，将原来的曲线分为两段，分出来的两条曲线继续直线步骤1、2，直到所有的dmax < max。
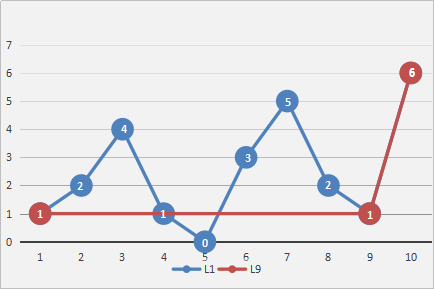
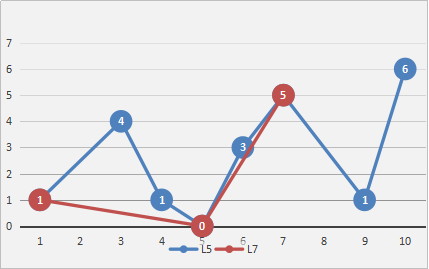
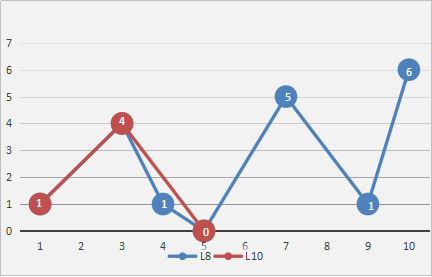
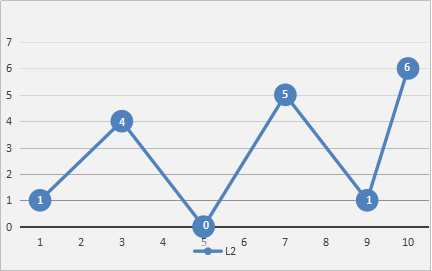
显然，算法的抽稀精读是和阈值相关的，阈值越大，舍弃的点越多，提取的关键点越少。若绘制的轨迹较长，可在对地图进行缩放时动态调整阈值。
算法原理
/** * gps轨迹抽稀算法 * @author: Z1hgq */ /** * 点到直线的距离，直线方程为 ax + by + c = 0 * @param {Number} a 直线参数a * @param {Number} b 直线参数b * @param {Number} c 直线参数c * @param {Object} xy 点坐标例如{ lat: 2, lng: 2 } * @return {Number} */ function getDistanceFromPointToLine(a, b, c, xy) { const x = xy.lng; const y = xy.lat; return Math.abs((a * x + b * y + c) / Math.sqrt(a * a + b * b)); } /** * 根据两个点求直线方程 ax+by+c=0 * @param {Object} xy1 点1,例如{ lat: 1, lng: 1 } * @param {Object} xy2 点2,例如{ lat: 2, lng: 2 } * @return {Array} [a,b,c] 直线方程的三个参数 */ function getLineByPoint(xy1, xy2) { const x1 = xy1.lng; // 第一个点的经度 const y1 = xy1.lat; // 第一个点的纬度 const x2 = xy2.lng; // 第二个点的经度 const y2 = xy2.lat; // 第二个点的纬度 const a = y2 - y1; const b = x1 - x2; const c = (y1 - y2) * x1 - y1 * (x1 - x2); return [a, b, c]; } /** * 稀疏点 * @param {Array} points 参数为[{lat: 1, lng: 2},{lat: 3, lng: 4}]点集 * @param {Number} max 阈值,越大稀疏效果越好但是细节越差 * @return {Array} 稀疏后的点集[{lat: 1, lng: 2},{lat: 3, lng: 4}]，保持和输入点集的顺序一致 */ function sparsePoints(points, max) { if (points.length < 3) { return points; } const xy1 = points[0]; // 取第一个点 const xy2 = points[points.length - 1]; // 取最后一个点 const [a, b, c] = getLineByPoint(xy1, xy2); // 获取直线方程的a,b,c值 let ret = []; // 最后稀疏以后的点集 let dmax = 0; // 记录点到直线的最大距离 let split = 0; // 分割位置 for (let i = 1; i < points.length - 1; i++) { const d = getDistanceFromPointToLine(a, b, c, points[i]); if (d > dmax) { split = i; dmax = d; } } if (dmax > max) { // 如果存在点到首位点连成直线的距离大于max的,即需要再次划分 // 按split分成左边一份，递归 const child1 = sparsePoints(points.slice(0, split + 1), max); // 按split分成右边一份，递归 const child2 = sparsePoints(points.slice(split), max); // 因为child1的最后一个点和child2的第一个点,肯定是同一个（即为分割点）,合并的时候,需要注意一下 ret = ret.concat(child1, child2.slice(1)); return ret; } else { // 如果不存在点到直线的距离大于阈值的,那么就直接是首尾点了 return [points[0], points[points.length - 1]]; } } export default sparsePoints;
效果展示
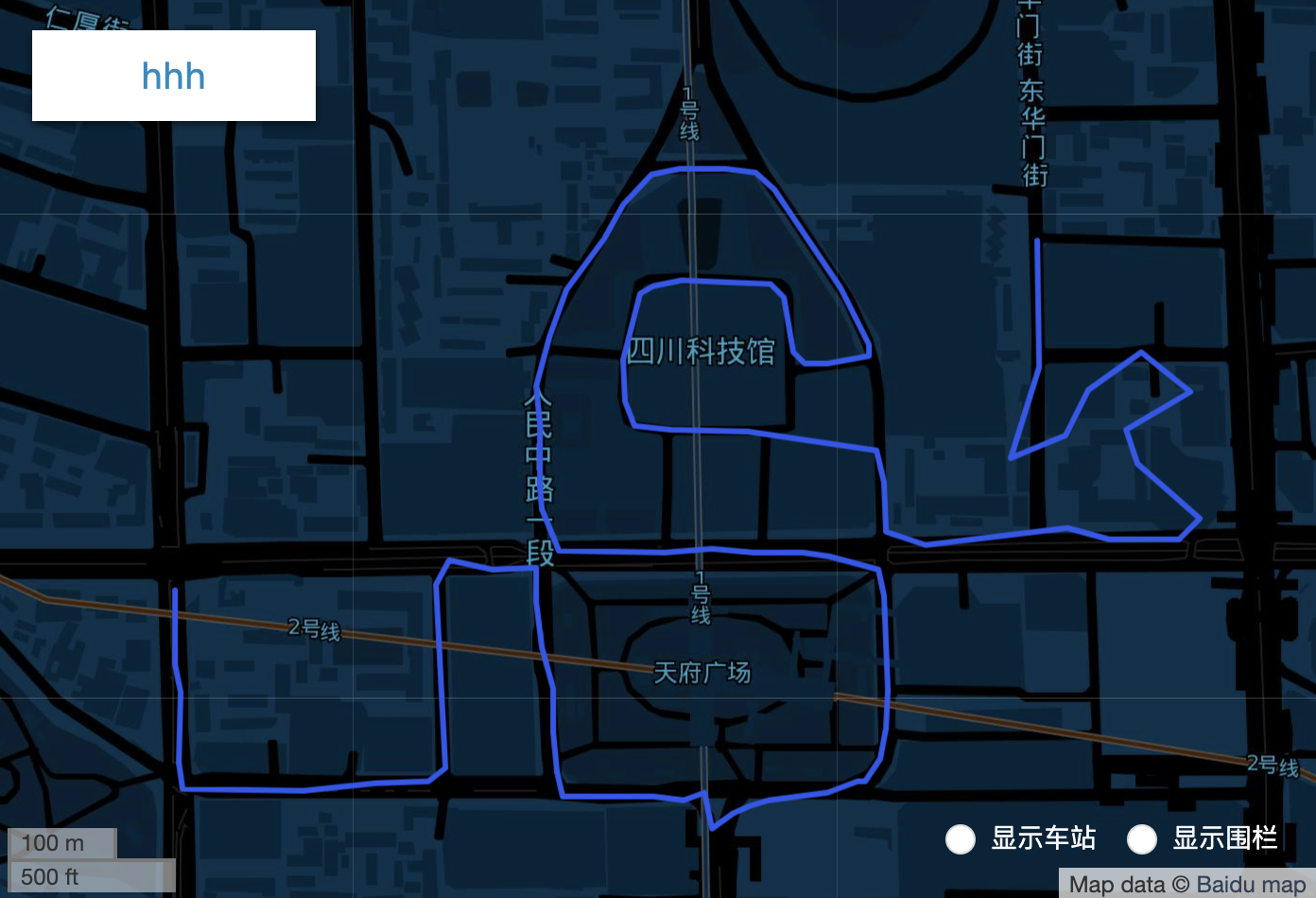
数据点类型为类似30.664147,104.067232，抽稀阈值为0.000005，第一张图为原始gps数据，共265个点，第二张图为抽稀之后的数据，共108个点。
