贝塞尔曲线的理解
Bezier曲线的由来
1962年,法国工程师贝塞尔发表,他运用贝塞尔曲线来为汽车的主体进行设计
Bezier曲线的作用
Bezier曲线是用一系列点控制曲线状态的。主要分为
- 数据点:确定曲线的起始和结束位置
- 控制点:确定曲线的弯曲程度
举例理解:想在AC(起始点和结束点)之间画一个曲线,用B点(控制点)控制这个曲线的弯曲程度


但是控制点是可以多个的,比如两个控制点。以此类推,可以有很多个。

起点和终点都只有一个,但是控制点可以多个,甚至是0,0的时候就是直线啦!
Bezier曲线的原理
为什么几个点就可以得到一个曲线?
先说一个控制点的情况,如图所示:

- A/B/C三点是确定的
- 在AB上任取一点D,得到ratio = AD/AB
- 再由BE/BC = ratio 得到E点
- 连接DE,同理DF/DE = ratio得到F
- 而F点就是曲线上的一点,当然凭着这一点是无法得到整条曲线的
- 于是,再来一遍,重新取D点得到新的F点,以此类推,如图

那么两个控制点呢?
道理是一样的,在AB上任取一点E,得到曲线上的J点。
AE/AB = BF/BC = CG/CD = EH/EF = FI/FG = HJ/HI



最后来个炫酷的四个控制点:

理解Bezier曲线的公式
一次贝塞尔曲线

一次贝塞尔曲线(也是线性贝塞尔曲线)公式:B(t) = (1 - t) * P0 + tP1
- t表示在 P0P1/P0P1之间任取一点P2,t = P0P2/P0P1,也就是比例,公式里的P0和P1同步表示其x轴坐标或者y轴坐标。
- 已知P0的坐标是(a,b),P1的坐标是(c,d),那么假设P2的坐标是(x,y)
- (1-t)/(c-x) = t/(x-a) => x = (1-t)a + tc
- 同理 y = (1-t)d + tb
- 于是简写成 B(t) = (1 - t) * P0 + tP1
二次贝塞尔曲线

- t同上
- 在P0P1上的点是A,在P1P2上的点是B,在AB上的点是C,C也就是曲线上的一点。
- A : tP1 + (1-t)P0
- B : tP2 + (1-t)P1
- C : tB + (1-t)A 将A、B换成上式,进行合并同类项
最后得到
同理可得三次贝塞尔曲线:



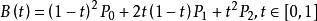

 浙公网安备 33010602011771号
浙公网安备 33010602011771号