插值技术研究
过采样与欠采样&图像重采样（上采样&下采样）
研究图像插值技术：2016年苏州大学的钟宝江等人《图像插值技术综述》[1]
图像插值利用图像已知采样点的灰度值估计未知采样点的灰度值，是图像数据的一种生成过程 。 图像插值的目的在于通过升采样的方式提高图像的分辨率。
插值分类
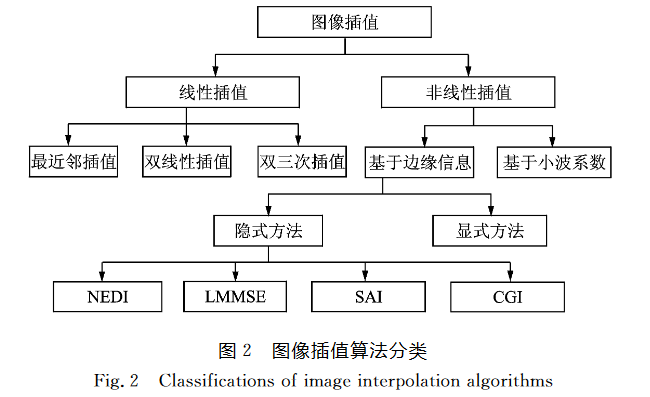
线性插值
1. 最邻近插值
取待插值点周围４个相邻像素点中欧式距离最短的一个邻点的灰度值作为该点的灰度值。
2. 双线性插值
插值原理是待插点像素值取原图像中与其相邻的4个点像素值的水平、垂直两个方向上的线性内插，即根据待采样点与周围4个邻点的距离确定相应的权重，从而计算出待采样点的像素值。
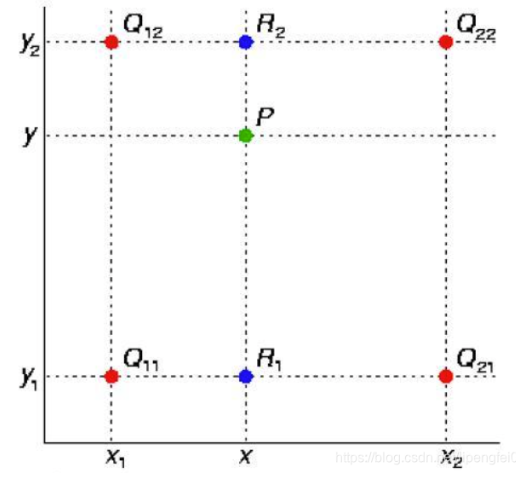[2]
remark: 双线性插值对于不在网格点上的待插值点有效，对于高度向稀疏所要补全的点都是在网格上的，则与一般的线性插值无区别。
3. 双三次插值
原理是利用以采样点为中心的4×4邻域内的16个已知像素点的灰度值来估计采样点的灰度值。双三次插值法不仅考虑到4个直接相邻点的灰度影响，而且考虑到各邻点间灰度值变化率的影响。
查看MATLAB的函数imresize()，支持三种线性插值方法[3]:
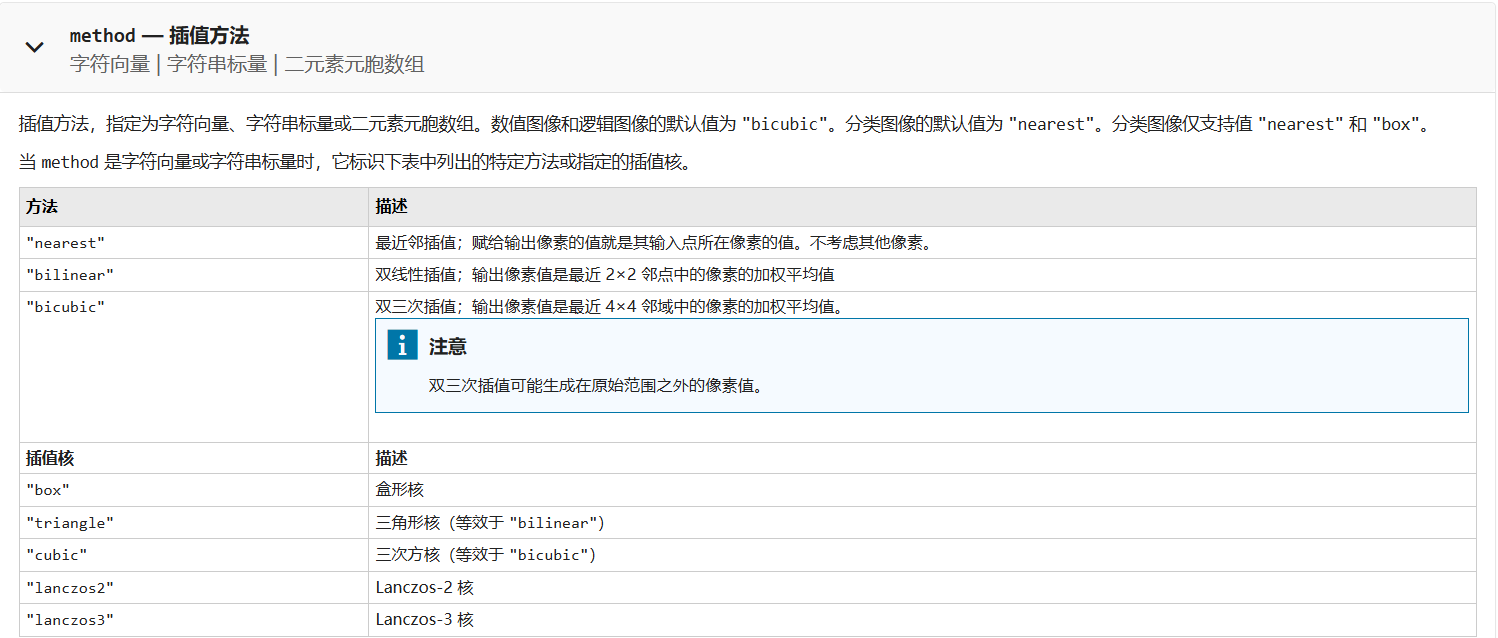
非线性插值
1. 基于小波系数的插值
基本思想是将信号分解到不同的 尺度或者分辨率层上，这样可以在不同的尺度上独立的对信号进行研究和分析。
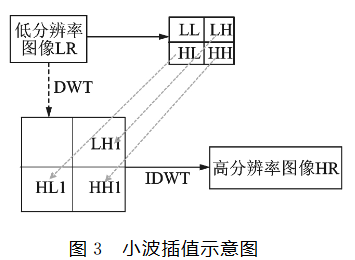
2. 基于边缘信息的插值
多项式插值（线性插值的推广[4]）
定义：多项式插值是线性插值的推广。线性插值是一个线性函数，我们现在用一个更高阶的多项式代替这个插值。
优点：一般情况下，如果我们有n个数据点，那么在所有的数据点中只有一个最多n-1次多项式可以完美拟合。此外，插值是一个多项式，因此是无限可微的。所以我们看到多项式插值克服了线性插值的大部分问题。
局限：与线性内插相比，计算内插多项式的成本是昂贵的。此外，多项式插值可能会出现振荡伪像，特别是在端点（高次插值会产生龙格现象[5]，当点数n 增大（次数m=n-1 也增大）时，有时会在两端产生激烈的震荡，出现函数不收敛的现象，即在两端处波动极大,产生明显的震荡）
1. 牛顿插值法
牛顿插值法通过计算差商确定多项式函数的系数[6]。
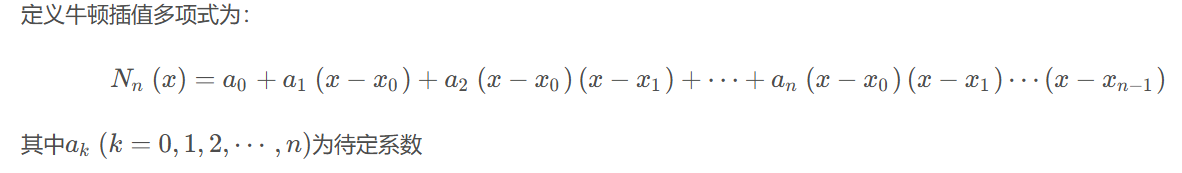
实验结果：
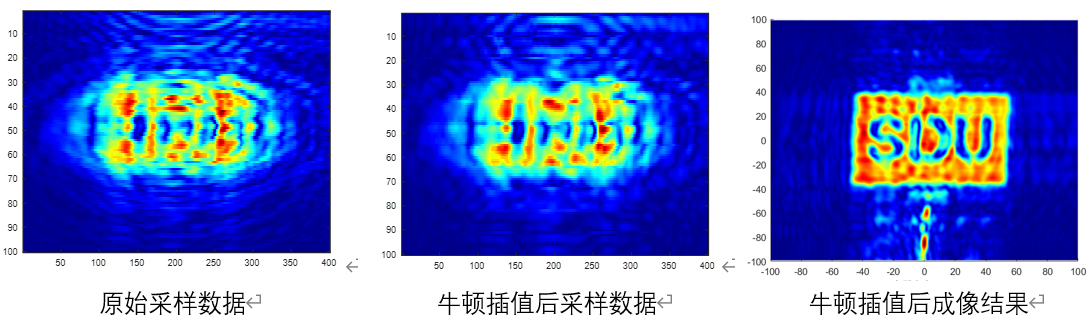
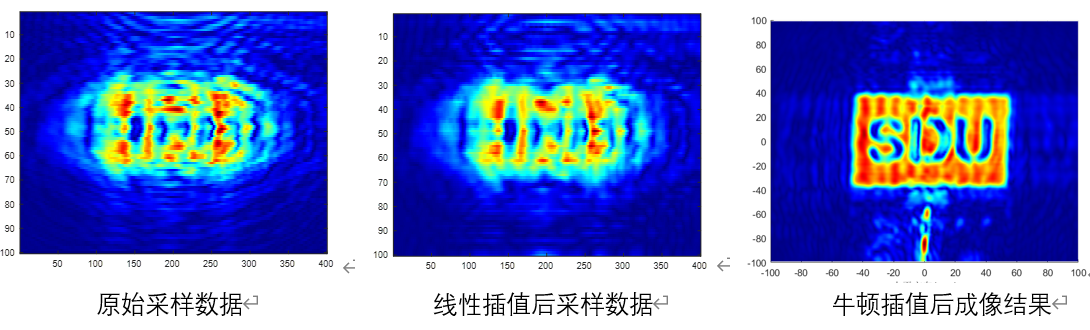
相比线性插值，牛顿插值也没有展现更多特别的优势和好处。
2. 拉格朗日插值[7]
实验结果：
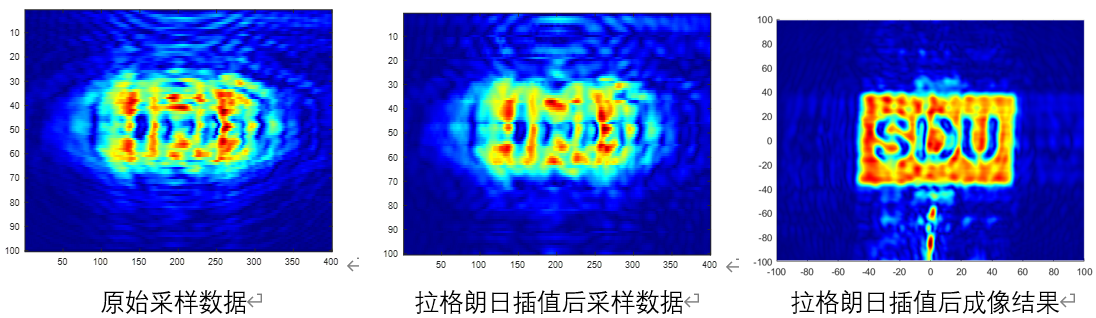
对比：
牛顿插值和拉格朗日插值：拉格朗日插值法和牛顿插值法插值出来的曲线一致，这两种插值方法只根据数值进行插值，不考虑方向，插值的曲线方向变化单一。牛顿插值法是拉格朗日插值法的改进方法，克服了拉格朗日插值法中存在的“增加一个节点时整个计算工作重新开始”的问题，且可以节省乘除法运算次数。拉格朗日插值法的基本思想就是使用多个取值点确定拉格朗日插值基，也就是所谓的插值系数[8]。
3. 三次样条插值[9]
4. Hermite（埃尔米特）插值[10]
5. Sinc插值
sinc插值算法,又叫香农插值算法(whittaker-shannon interpolation formula),是一种用于从离散实信号构造时间连续带限函数的方法[11]。
[12]
插值也是要求原数据是满足采样定律的。
对时域信号的采样得到的是离散的序列，在频域的表现就是原信号频谱的周期延拓，对频率加窗[13]（不同的卷积核）提取基带一个周期从而重建原始信号。
但要是原信号已经是由于欠采样导致混叠后，也就无法提取出一个完整且争取的周期频谱了。
参考：
钟宝江,陆志芳,季家欢.图像插值技术综述[J].数据采集与处理,2016,31(06):1083-1096. ↩︎
https://ww2.mathworks.cn/help/matlab/ref/imresize.html#d126e730731 ↩︎
