如何使用Soft-NMS实现目标检测并提升准确率
非极大值抑制(Non-Maximum suppression,NMS)是物体检测流程中重要的组成部分。它首先基于物体检测分数产生检测框,分数高的检测框M被选中,其他与被选中检测框又明显重叠的检测框被抑制。该过程不断递归的应用于其余检测框。根据算法设计,如果一个物体处于预设的重叠阈值之内,可能会导致检测不到该待检测物体。因此,我们提出了Soft-NMS算法,该连续函数对非最大检测框的检测分数进行衰减而彻底移除。它仅需要对传统的NMS算法进行简单的改动而且不增加额外的参数。该Soft-NMS具有与传统NMS相同的算法复杂度,使用高校。Soft-NMS也不需要额外的训练,并易于实现,它可以轻松的被集成到任何物体检测流程中。
NMS算法介绍
物体检测是计算机视觉领域的一个经典问题,它为特定类别的物体产生检测边框并且对分类打分。传统的物体检测流程常常采用多尺度滑动窗口,根据每个物体类别的前景/背景分数对每个窗口计算其特征。然而,相邻窗口往往具有相关的分数,这会增加检测结果的假阳性,为了避免这样的问题,人们会采用非极大值抑制的方法对检测结果进行后续处理来得到最终的检测结果。目前为止,非极大值抑制算法仍然是流行的物体检测处理算法并能有效的降低检测结果的假阳性。
如下图所示,物体检测框图中,每一个检测框均会产生检测分数,那么对于图片中的一个物体可能对应多个检测分数。这种情况下,除了最正确(检测分数最高)的一个检测框,其余的检测框均产生假阳性结果。非最大值抑制算法针对特定物体类别分别设定重叠阈值来解决这个问题。

传统的非最大值抑制算法首先在被检测图片中产生一系列的检测框B以及对应的分数S。当选中最大分数的检测框M,它被从集合B中移出并放入最终检测结果集合D。与此同时,集合B中任何与检测框M的重叠部分大于重叠阈值Nt的检测框也没随之移除。非极大值抑制算法中的最大问题就是它将相邻检测框的分数均强制归零。在这种情况下,如果一个真实的物体在重叠区域出现,则将会导致对该物体的检测失败并降低类算法的平均检测率(mAP)
换一种思路,如果我们只是通过一个基于与M重叠程度相关的函数来降低相邻检测框的分数而非彻底剔除。虽然分数被降低,单相邻的检测框仍然在物体检测的序列中。下图的实例可以说明这个问题。

Soft-NMS可提升目标检测的平均准确率
针对NMS存在的这个问题,我们提出了一种新的Soft-NMS算法,它秩序改动一行代码即可有效的改进传统贪心NMS算法。在该算法中,我们基于重叠部分的大小为相邻检测框设置一个衰减函数而非彻底将其分数置为0。简单来讲,如果一个检测框与M有大部分重叠,它会有很低的分数,而如果检测框与M只有小部分重叠,那么它的原有检测分数不会受太大影响。在标准数据集Pascal VOC和MS-COCO等标准数据集上,Soft-NMS对现有的物体检测算法在多个重叠物体检测的平均准确率有明显显著的提升。同时Soft-NMS不需要额外的训练且易于实习那,因此,它很容易被集成到目前的检测流程中。

Soft-NMS伪代码,仅需要将NMS代码(红色框)替换为Soft-NMS代码(绿色框)一步即可完成
传统的NMS处理方法可以通过以下的分数重置函数(Rescoring Function)来表达:
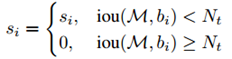
在这个公式中,NMS采用类硬阈值来判断相邻检测框是否保留。但是换一种方法,假设我们对一个与M高度重叠的检测框bi的检测分数进行衰减,而非全部抑制。如果检测框bi中包含不同于M中的物体,那么在检测阈值比较低的情况下,该物体并不会错过检测,但是,如果bi中并包含任何物体,即使在衰减过后,bi的分数仍然较高,它还是会产生一个假阳性的结果。因此,在使用NMS做物体检测处理的时候,需要注意一下几点:
- 相邻检测框的检测分数应该被降低,从而减少假阳性结果,但是衰减后的分数仍然应该比明显的假阳性结果要高
- 通过较低的NMS重叠阈值来移除所有相邻检测框并不是最优解,并且很容易错过被检测物体,特别是在物体高度重叠的地方
- 当NMS采用一个较高的重叠阈值时,平均准确率可能会相应的降低
Soft-NMS中的分数重置函数
通过衰减与检测框M有重叠的相邻检测框的分数是对NMS算法的有效改进。越是与M高度重叠的检测框,越有可能会出现假阳性结果,它们的分数衰减应该更严重。因此作者对NMS原有的分数重置函数做如下改进:
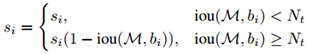
当相邻检测框与M的重叠度超过重叠阈值Nt后,检测框分数成线性衰减。但是上述分数重置函数并不是一个连续函数,在重叠程度超过重叠阈值Nt时,该分数重置函数产生突变,从而可能导致检测结果序列产生大的变动,因此我们更希望找到一个连续的分数重置函数。它对没有重叠的检测框的原有检测分数不产生衰减,同时对高度重叠的检测框产生大的衰减。综合考虑这些因素,作者进一步对soft-NMS中的分数重置函数进行了改进:
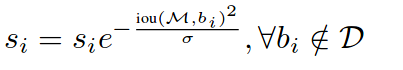
算法的每一步的复杂度为O(N),N为图片中检测框的数量。对于N个检测框,Soft-NMS的算法复杂度为O(N^2),与传统的贪心NMS算法相同。由于分数低于一个最小阈值的检测框会被直接剔除,因此NMS并不需要对所有检测框进行操作,计算量并不庞大,也不会减慢当前检测器的运行速度。
值得注意的是,Soft-NMS也是一种贪心算法,并不能保证找到全局最优的检测框分数重置。但是Soft-NMS算法是一种更加通用的非最大抑制算法,传统NMS算法可以看做是它的一个采用不连续二值权重函数的特例。除了以上两种分数重置函数,我们也可以考虑开发其他包含更多参数的分数重置函数,比如Gompertz函数等。但是它们在完成分数重置的过程中增加类额外的参数。





