算法(双指针|动态规划)

双指针技巧

167 两数之和

输入一个升序的有序数组,找到两数的和等于目标值

const twoSum = (numbers, target) => {
  let start = 0
  let end = numbers.length - 1
  while (start < end) {
    let sum = numbers[start] + numbers[end]
    if (sum == target) {
      return [start + 1, end + 1]
    }
    if (sum > target) {
      end--
      continue
    }
    if (sum < target) {
      start++
      continue
    }
  }
}
console.log(twoSum([1, 2, 3, 4, 5, 6], 11))

125 验证回文串

只考虑数字和字母

//如果遇到不是数字后者字母直接跳过
const isPalindrome = s => {
  let start = 0,
    end = s.length - 1;
  let reg = /[a-z0-9]/
  while (start < end) {
    const pre = s[start].toLowerCase()
    const suf = s[end].toLowerCase()
    if (!reg.test(pre)) {
      start++
      continue
    }
    if (!reg.test(suf)) {
      end--
      continue
    }
    if (pre !== suf) {
      return false
    }
    start++
    end--
  }
  return true
}
console.log(isPalindrome('abba'))

双向冒泡排序

const bubbleSort = arr => {
    let isSwap = '',tail=arr.length-1
    for (let i = 0; i < tail; i++) {
        isSwap = false
        for (let j = tail; j > i; j--) {
            if (arr[j] > arr[j + 1]) {
                isSwap = true
                swap(j, j + 1, arr)
            }
        }
        for (let j = i; j < tail; j++) {
            if (arr[j] > arr[j + 1]) {
                isSwap = true
                swap(j, j + 1, arr)
            }
        }
        if (!isSwap) {
            break
        }
    }
    return arr
}
console.log(bubbleSort([1, 10, 3, 4, 5, 6, 1221, 1, 2, 3, 4, 4, 5]))

41 给定一个未排序的整数数组，找出其中没有出现的最小的正整数

输入: [1,2,0]
输出: 3
示例 2:

输入: [3,4,-1,1]
输出: 2
示例 3:

输入: [7,8,9,11,12]
输出: 1

采用集合

const firstMissing = nums => {
    const set = new Set()
    for (let i = 0; i < nums.length; i++) {
        if (nums[i] >= 0&& nums[i] <= nums.length) {
            set.add(nums[i])
        }
    }
    for (let i = 0; i <= nums.length; i++) {
        if (!set.has(i)) {
            return i
        }
    }
    return nums.length
}

我自己改的

const firstMissing = nums => {
    if (nums == null || nums.length < 1)
        return 1
    let a = nums.filter(v => v > 0).sort((a, b) => a - b)
    let s = 1
    while (s < a.length) {
        if (s < a[s - 1]) {
            return s
        }
        s++
    }
}

如何在 10 亿数中找出前 1000 大的数

const firstMissing = nums => {
    let i = 1
    while (1) {
        if (nums[i] > 1000) {
            return nums[i]
        }
        if (!(typeof nums[i] == "number")) {
            return '不好意思没有找到'
        }
        i++
    }
}

贪心算法

中心思想: 大事化小,小事化了

动态规划

通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法

总结就是:

  • 有最优解的结构

  • 找到子问题

  • 以"自底向上"的方式计算最优解的值

  • 可以从已计算的信息中构建出最优的路径

最少硬币数

确定状态

最后一步(最优策略种使用的最后一枚硬币ak)

化成子问题(最少的硬币拼出最小的面值27-ak)

转移方程

f[x]=Math.min(f[x-2]+1,f[x-5]+1,f[x-7]+1)

初始化条件和边界情况

f[0]=0,如果不能评出Y,f[Y]=正无穷

计算顺序

从小到大

const coinChange = (A, M) => {
  let n = A.length;
  let f = [];
  f[0]=0
  for (let i = 1; i <= M; i++) {
    //选择硬币
    f[i] = Infinity
    for (let j = 0; j < n; j++) {
      //i>=A[j] 你的硬币不能大于我的目标值,相当于我要拼出10块钱,你不能为11块钱
      //i-A[j] 11-1,-3,-5 的值
      if (i >= A[j] && f[i - A[j]] != Infinity && f[i - A[j]] + 1 < f[i]) {
        f[i] = f[i - A[j]] + 1
      }
      console.log(f)
    }
  }
  if (f[M] == Infinity) {
    return -1
  } else {
    return f[M]
  }
}
console.log(coinChange([1,2,5], 15))

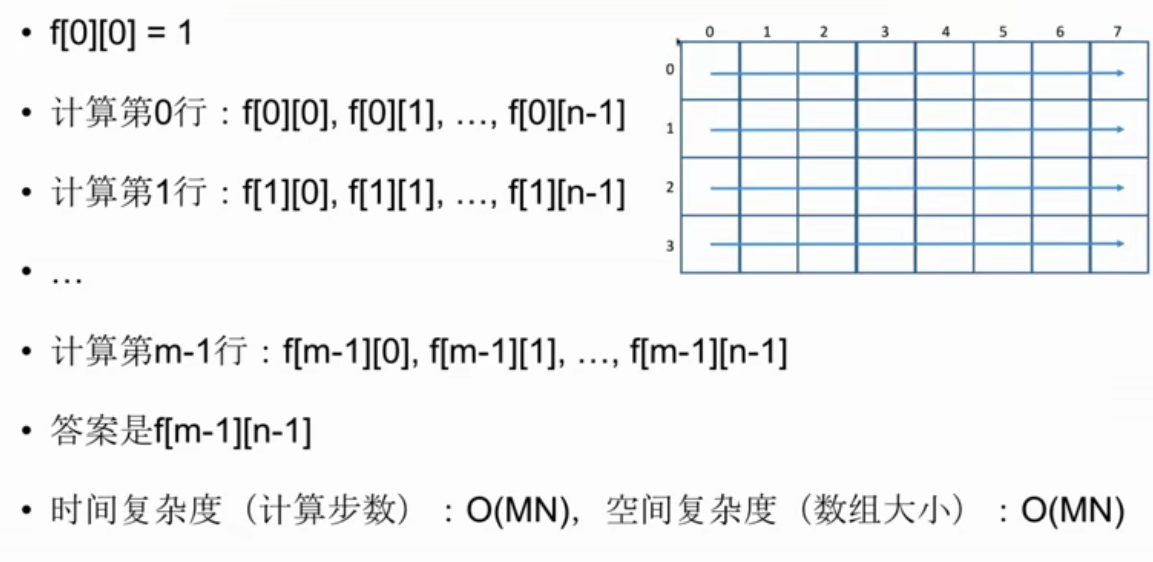
114

给定m行n列的网格,有一个机器人从左上角(0,0)出发,每一步可以向下或者向有走一步,

问有多少种不同的方式

确定状态

  • 左下角左边设为(m-1,n-1)
  • 那么前一步机器人一定是再(m-2,n-1)或者(m-1,n-2)

子问题

  • 那么机器人有x种方式从左上角走到(m-2,n-1)

  • 有y种方式从左上角走到(m-1,n-2)

  • 则机器人有x+y种方式走到(m-1,n-1)

转化方程

对于任意一个格子(i,j)

f[i][j]=f[i-1][j]+f[i][j-1]

有多少种方式走到(i,j)=(i-1,j)+(i,j-1)

初始条件和边界情况

  • 初始条件:f[0][0]=1 因为机器人只有一种方式到左上角
  • 边界情况: i=0 或 j=0 则前一步只能有一个方向过程f[i][j]=1

计算顺序

const Solution = (m, n) => {
  let f = Array.from({length:m},v=>[])
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      //按照行列的情况进行循环
      if (i == 0 || j == 0) {
        f[i][j] = 1;
      } else {
        f[i][j] = f[i - 1][j] + f[i][j - 1]
      }
    }
  }
  return f[m - 1][n - 1]
}
console.log(Solution(3, 3))

116

有n块石头分别在x轴的0,1,...n-1位置

一只青蛙在石头0,想跳到石头n-1

如果青蛙在第i块石头上,他最多可以向右跳距离a[j]

问青蛙能够跳到石头n-1

例子
[2,3,1,1,4]
true
[3,2,1,0,1]
false

存在型动态规划

确定状态

最后一步:如果青蛙能跳到最后一块石头n-1,那我们考虑他跳的最后一步

这一步是从石头i调过来,i<n-1

需要两个条件同时满足:

  • 青蛙可以跳到石头i
  • 最后一步不超过跳跃的最大距离:n-1-i<a[j]

子问题

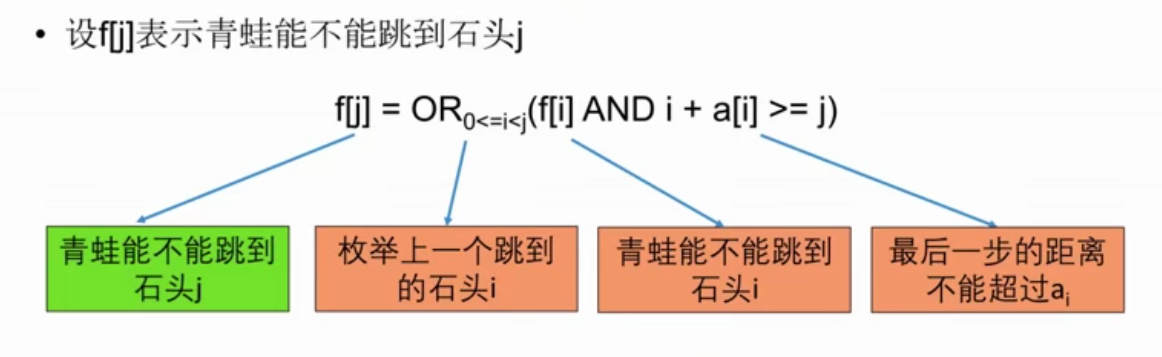
状态:设f[j]表示青蛙能不能跳到石头j

转移方程

计算顺序

const Solution = A => {
  if (A == null || A.length == 0) {
    return false
  }
  let f = [true,]
  for (let i = 1; i < A.length; i++) {
    f[i] = false
    for (let j = 0; j < i; j++) {
      if (f[j] && (j + A[j]) >= i) {
        f[i] = true
        break
      }
    }
  }
  return f[A.length-1]
}
console.log(Solution([2, 3, 1, 1, 4]))
console.log(Solution([3,2,1,0,4]))


###########################...................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

posted @ 2019-07-08 14:40  猫神甜辣酱  阅读(937)  评论(0)  编辑  收藏  举报