算法(平衡二叉树)
科普二叉树
二叉树
二叉数是每个节点最多有两个子树,或者是空树(n=0),或者是由一个根节点及两个互不相交的,分别称为左子树和右子树的二叉树组成
满二叉树
有两个非空子树(二叉树中的每个结点恰好有两个孩子结点切所有叶子结点都在同一层)
也就是一个结点要么是叶结点,要么是有两个子结点的中间结点。
深度为k且含有2^k-1个结点的二叉树
完全二叉树
从左到右依次填充
从根结点开始,依次从左到右填充树结点。
除最后一层外,每一层上的所有节点都有两个子节点,最后一层都是叶子节点。
平衡二叉树
AVL树
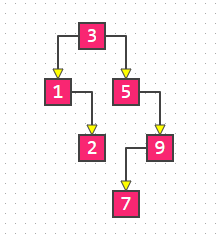
[3,1,2,5,9,7]首先科普下二叉排序树又称二叉查找树,议程二叉搜索树
二叉排序树的规则
比本身大放右边,比本身小放左边
平衡二叉数
- 首先是一个二叉排序树
- 左右两个子树的高度差不大于1
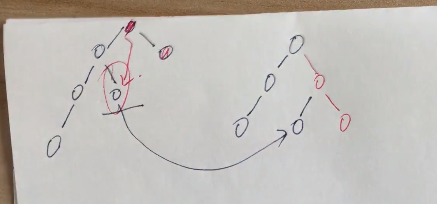
下面图中是平衡的情况
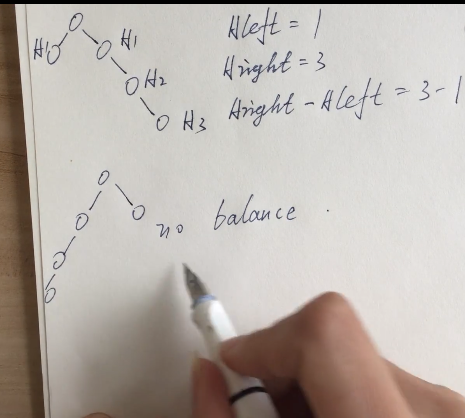
下面是不平衡的情况
引入公式
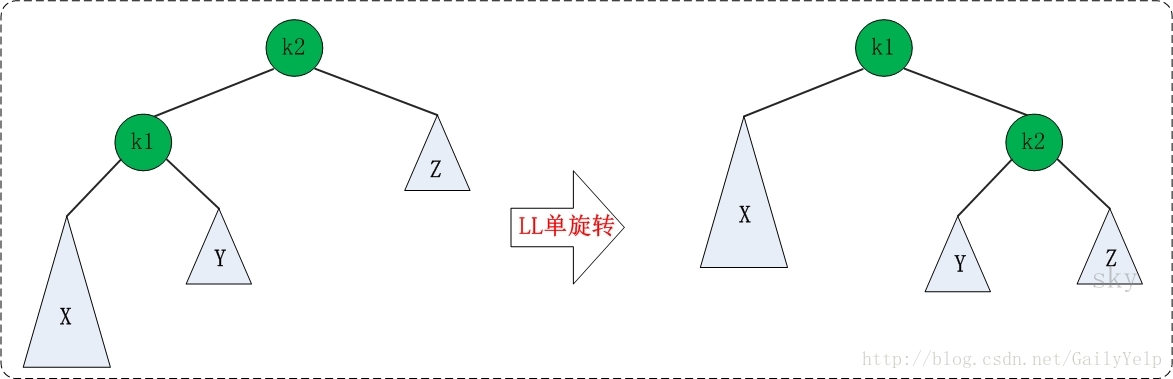
(LL)右旋
function toateRight(AvlNode){ let node=AvlNode.left;//保存左节点 AvlNode.left=node.right; node.right=AvlNode; }
(RR)左旋
function roateLeft(AvlNode){ let node=AvlNode.right;//保存右子节点 AvlNode.right=node.left; node.left=AvlNode; return node; }
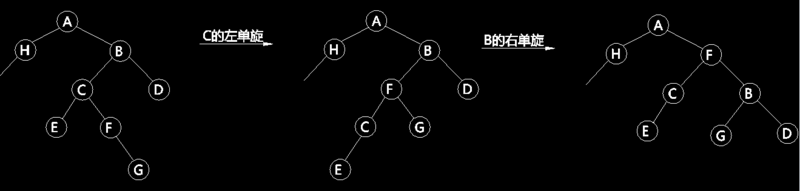
左右旋
大图

判断二叉树是不是平衡树
二叉树任意结点的左右子树的深度不超过1
深度计算
定义一个初始化的二叉树 var nodes = { node: 6, left: { node: 5, left: { node: 4 }, right: { node: 3 } }, right: { node: 2, right: { node: 1 } } }//计算高度 const treeDepth = (root) => { if (root == null) { return 0; } let left = treeDepth(root.left) let right = treeDepth(root.right) return 1+(left>right?left:right) } //判断深度 const isTree=(root)=>{ if (root == null) { return true; } let left=treeDepth(root.left) let right=treeDepth(root.right) let diff=left-right; if (diff > 1 || diff < -1) { return false } return isTree(root.left)&&isTree(root.right) } console.log(isTree(nodes))
判断二叉数是不是搜索二叉树
//第一种 //中序遍历
let last=-Infinity;
const isValidBST=(root)=>{
if (root == null) {
return true;
}
//先从左节点开始
if (isValidBST(root.left)) {
if (last < root.node) {
last=root.node;
return isValidBST(root.right)
}
}
return false
}
console.log(isValidBST(nodes))
//第二种
const isValidBST = root => {
if (root == null) {
return true
}
return dfs(root, -Infinity, Infinity)
}
const dfs = (root, min, max) => {
if (root == null) {
return true
}
if (root.node <= min || root.node >= max) {
return false
}
return dfs(root.left, min, root.node) && dfs(root.right, root.node, max)
}
console.log(isValidBST(nodes))
实现一个二叉树
实现了二叉树的添加,删除,查找,排序
//二叉树结点
class TreeNode {
constructor(n, left, right){
this.n = n;
this.left = left;
this.right = right;
}
}
//二叉树
class BinaryTree {
constructor(){
this.length = 0;
this.root = null;
this.arr = [];
}
//添加对外入口,首个参数是数组,要求数组里都是数字,如果有不是数字则试图转成数字,如果有任何一个无法强制转成数字,则本操作无效
addNode(){
let arr = arguments[0];
if(arr.length == 0) return false;
return this.judgeData('_addNode', arr)
}
//删除结点
deleteNode(){
let arr = arguments[0];
if(arr.length == 0) return false;
return this.judgeData('_deleteNode', arr)
}
//传值判断,如果全部正确,则全部加入叉树
judgeData(func, arr){
let flag = false;
//任何一个无法转成数字,都会失败
if(arr.every(n => !Number.isNaN(n))){
let _this = this;
arr.map(n => _this[func](n));
flag = true;
}
return flag;
}
//添加的真实实现
_addNode(n){
n = Number(n);
let current = this.root;
let treeNode = new TreeNode(n, null, null);
if(this.root === null){
this.root = treeNode;
}
else {
current = this.root;
while(current){
let parent = current;
if(n < current.n){
current = current.left;
if(current === null){
parent.left = treeNode;
}
}
else {
current = current.right;
if(current === null){
parent.right = treeNode;
}
}
}
}
this.length++;
return treeNode;
}
//删除节点的真实实现
_deleteNode(n){
n = Number(n);
if(this.root === null){
return;
}
//查找该节点,删除节点操作比较复杂,为排除找不到被删除的节点的情况,简化代码,先保证该节点是存在的,虽然这样做其实重复了一次查询了,但二叉树的查找效率很高,这是可接受的
let deleteNode = this.findNode(n);
if(!deleteNode){
return;
}
//如果删除的是根节点
if(deleteNode === this.root){
if(this.root.left === null && this.root.right === null){
this.root = null;
}
else if(this.root.left === null){
this.root = this.root.right;
}
else if(this.root.right === null){
this.root = this.root.left;
}
else {
let [replaceNode, replacePNode, rp] = this.findLeftTreeMax(deleteNode);
replacePNode[rp] = null;
replaceNode.left = this.root.left;
replaceNode.right = this.root.right;
this.root = replaceNode;
}
}
else {
//被删除的父节点,子节点在父节点的位置p,有left,right两种可能
let [deleteParent, p] = this.findParentNode(deleteNode);
if(deleteNode.left === null && deleteNode.right === null){
deleteParent[p] = null;
}
else if(deleteNode.left === null){
deleteParent[p] = deleteNode.right;
}
else if(deleteNode.right === null){
deleteParent[p] = deleteNode.left;
}
else {
//用来替换被删除的节点,父节点,节点在父节点的位置
let [replaceNode, replacePNode, rp] = this.findLeftTreeMax(deleteNode);
if(replacePNode === deleteNode){
deleteParent[p] = replaceNode;
}
else {
deleteParent[p] = replaceNode;
replacePNode.right = null;
}
replacePNode[rp] = null;
replaceNode.left = deleteNode.left;
replaceNode.right = deleteNode.right;
}
}
this.length--;
}
//查找
findNode(n){
let result = null;
let current = this.root;
while(current){
if(n === current.n){
result = current;
break;
}
else if(n < current.n){
current = current.left;
}
else {
current = current.right;
}
}
return result;
}
//查找父节点
findParentNode(node){
let [parent, child, p] = [null, null, null];
if(this.root !== node){
parent = this.root;
if(node.n < parent.n){
child = parent.left;
p = 'left';
}
else {
child = parent.right;
p = 'right';
}
while(child){
if(node.n === child.n){
break;
}
else if(node.n < child.n){
parent = child;
child = parent.left;
p = 'left';
}
else {
parent = child;
child = parent.right;
p = 'right';
}
}
}
return [parent, p];
}
//查找当前有左子树的节点的最大值的节点M,如有A个节点被删除,M是最接近A点之一(还有一个是右子树节点的最小值)
findLeftTreeMax(topNode){
let [node, parent, p] = [null, null, null];
if(this.root === null || topNode.left === null){
return [node, parent, p];
}
parent = topNode;
node = topNode.left;
p = 'left';
while(node.right){
parent = node;
node = node.right;
p = 'right';
}
return [node, parent, p];
}
//查找最大值
maxValue(){
if(this.root !== null){
return this._findLimit('right');
}
}
//查找最小值
minValue(){
if(this.root !== null){
return this._findLimit('left');
}
}
//实现查找特殊值
_findLimit(pro){
let n = this.root.n;
let current = this.root;
while(current[pro]){
current = current[pro];
n = current.n;
}
return n;
}
//中序排序,并用数组的形式显示
sortMiddleToArr(){
this._sortMiddleToArr(this.root);
return this.arr;
}
//中序方法
_sortMiddleToArr(node){
if(node !== null){
this._sortMiddleToArr(node.left);
this.arr.push(node.n);
this._sortMiddleToArr(node.right);
}
}
//打印二叉树对象
printNode(){
console.log(JSON.parse(JSON.stringify(this.root)));
}
}
//测试
var binaryTree = new BinaryTree();
binaryTree.addNode([50, 24, 18, 65, 4, 80, 75, 20, 37, 40, 60]);
binaryTree.printNode();//{n: 50, left: {…}, right: {…}}
console.log(binaryTree.maxValue());//80
console.log(binaryTree.minValue());//4
console.log(binaryTree.sortMiddleToArr());// [4, 18, 20, 24, 37, 40, 50, 60, 65, 75, 80]
binaryTree.deleteNode([50]);
binaryTree.printNode();//{n: 40, left: {…}, right: {…}}
排序复习
function ArrayList() {
this.array = [];
}
ArrayList.prototype = {
constructor: ArrayList,
insert: function(item) {
this.array.push(item);
},
toString: function() {
return this.array.join();
},
swap: function(index1, index2) {
var aux = this.array[index2];
this.array[index2] = this.array[index1];
this.array[index1] = aux;
},
//冒泡排序
bubbleSort: function() {
var length = this.array.length;
for (var i = 0; i < length; i++) {
for (var j = 0; j < length - 1 - i; j++) {
if (this.array[j] > this.array[j + 1]) {
this.swap(j, j + 1);
}
}
}
},
//选择排序
selectionSort: function() {
var length = this.array.length;
var indexMin;
for (var i = 0; i < length - 1; i++) {
indexMin = i;
for (var j = i; j < length; j++) {
if (this.array[indexMin] > this.array[j]) {
indexMin = j;
}
}
if (indexMin !== i) {
this.swap(indexMin, i);
}
}
},
//插入排序
insertionSort: function() {
var length = this.array.length;
var j;
var temp;
for (var i = 1; i < length; i++) {
temp = this.array[i];
j = i;
while (j > 0 && this.array[j - 1] > temp) {
this.array[j] = this.array[j - 1];
j--;
}
this.array[j] = temp;
}
},
//归并排序
mergeSort: function() {
function mergeSortRec(array) {
var length = array.length;
if (length === 1) {
return array;
}
var mid = Math.floor(length / 2);
var left = array.slice(0, mid);
var right = array.slice(mid, length);
return merge(mergeSortRec(left), mergeSortRec(right));
}
function merge(left, right) {
var result = [];
var il = 0;
var ir = 0;
while (il < left.length && ir < right.length) {
if (left[il] < right[ir]) {
result.push(left[il++]);
} else {
result.push(right[ir++]);
}
}
while (il < left.length) {
result.push(left[il++]);
}
while (ir < right.length) {
result.push(right[ir++]);
}
return result;
}
this.array = mergeSortRec(this.array);
},
//快速排序
quickSort:function(){
function sort(array){
if (array.length <= 1) {
return array;
}
var pivotIndex = Math.floor(array.length/2);
var pivot = array.splice(pivotIndex,1)[0];
var left = [];
var right = [];
for(var i = 0; i < array.length; i++){
if (array[i] < pivot) {
left.push(array[i]);
}else{
right.push(array[i]);
}
}
return sort(left).concat([pivot],sort(right));
}
this.array = sort(this.array);
}
};
...................................................................................................................###############################################################################################################################################################
决定自己的高度的是你的态度,而不是你的才能
记得我们是终身初学者和学习者
总有一天我也能成为大佬



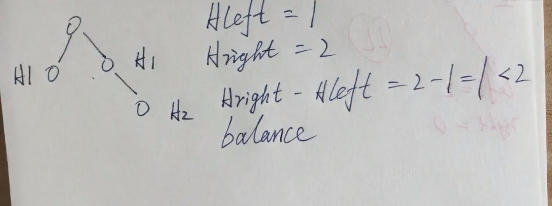


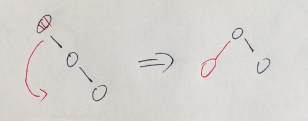




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 开源Multi-agent AI智能体框架aevatar.ai,欢迎大家贡献代码
· Manus重磅发布:全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!