算法 之平衡二叉树

宽容别人，其实也是给自己的心灵让路。

 

结构定义：（c语言）

typedef struct AVLNode *Tree;
typedef int ElementType;

struct AVLNode{
    int depth; //深度
    Tree parent; //父节点
    ElementType val; //结点值
    Tree lchild;
    Tree rchild;

    AVLNode(int val=0) {
        parent = NULL;
        depth = 0;
        lchild = rchild = NULL;
        this->val=val;
    }
};

　

特性：

• 可以是空树
• 假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过1

 

平衡因子：

某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子（BF,Balance Factor），平衡二叉树中不存在平衡因子大于1的节点。
在一棵平衡二叉树中，节点的平衡因子只能取0 、1或者-1，分别对应着左右子树等高，左子树比较高，右子树比较高。

 

平衡二叉树插入失衡调整

找对最小平衡树，然后通过左旋，右旋来进行调整

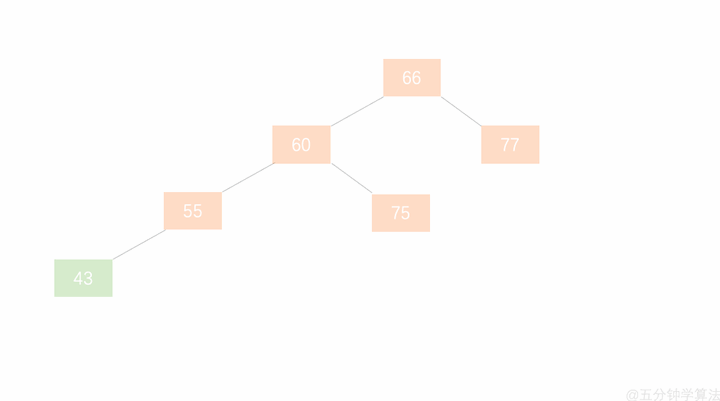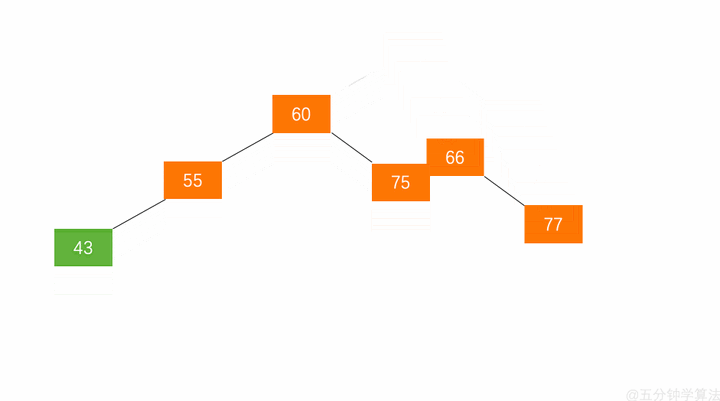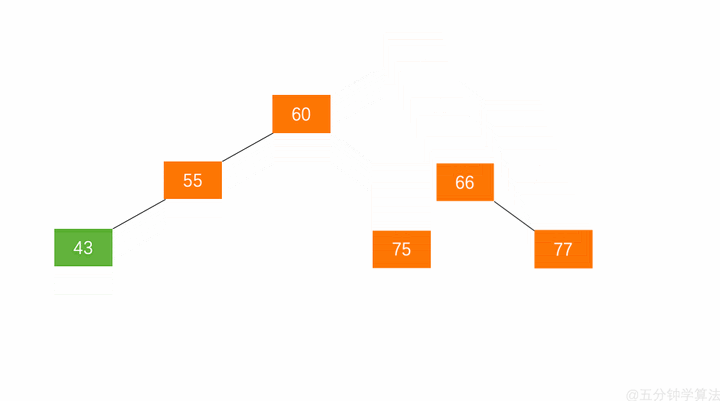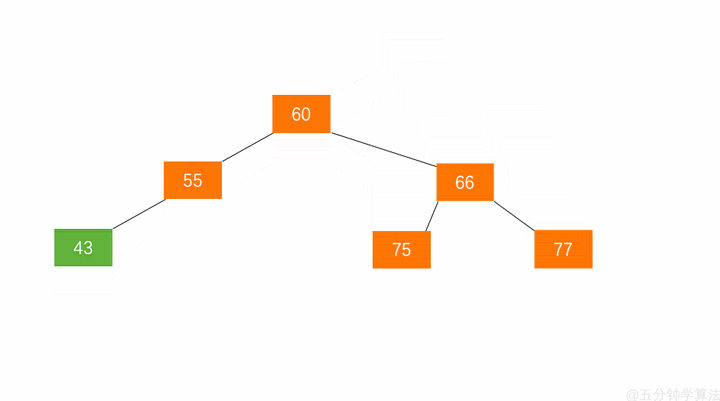
左旋步骤：

1. 节点的右孩子替代此节点位置
2. 右孩子的左子树变为该节点的右子树
3. 节点本身变为右孩子的左子树

如图

 

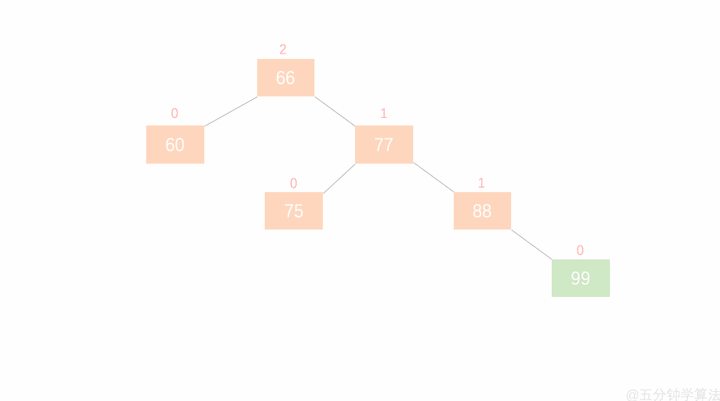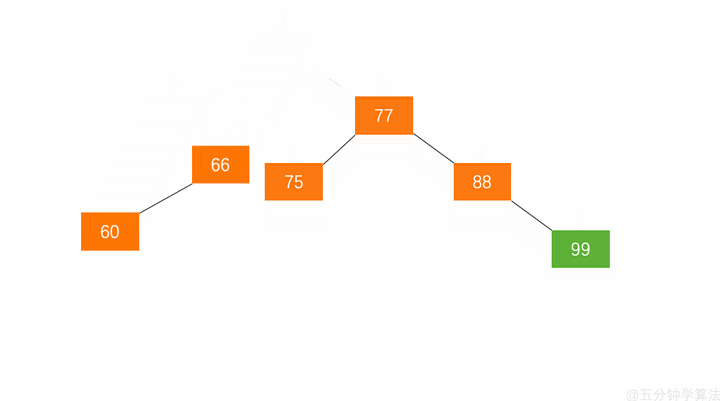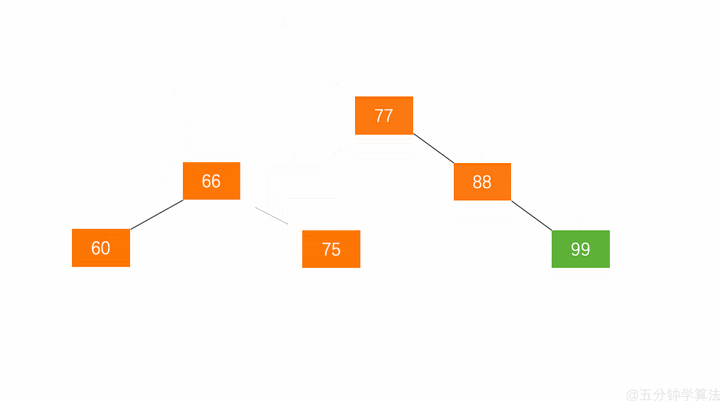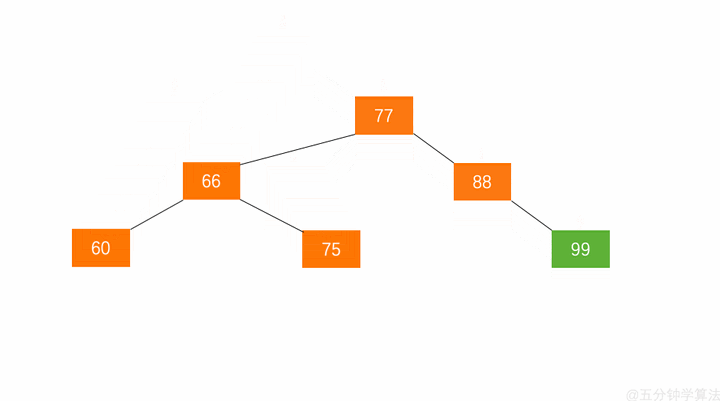
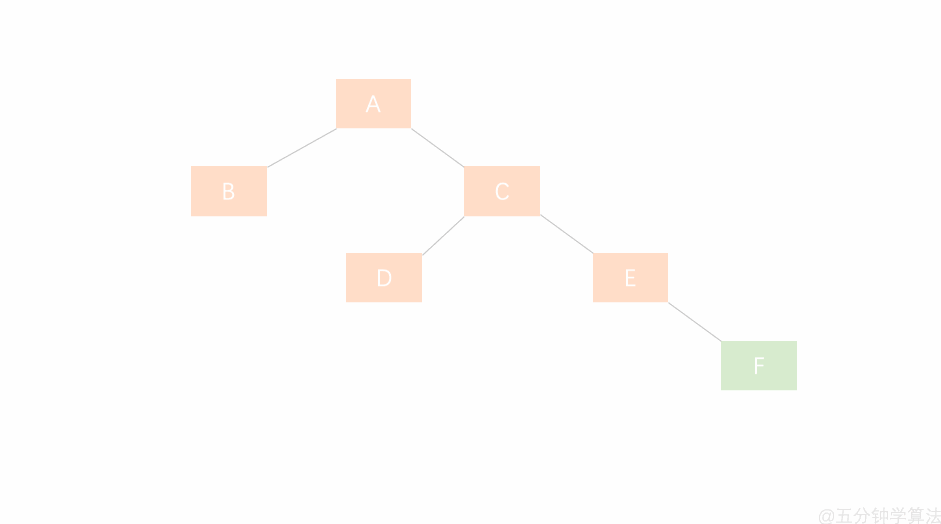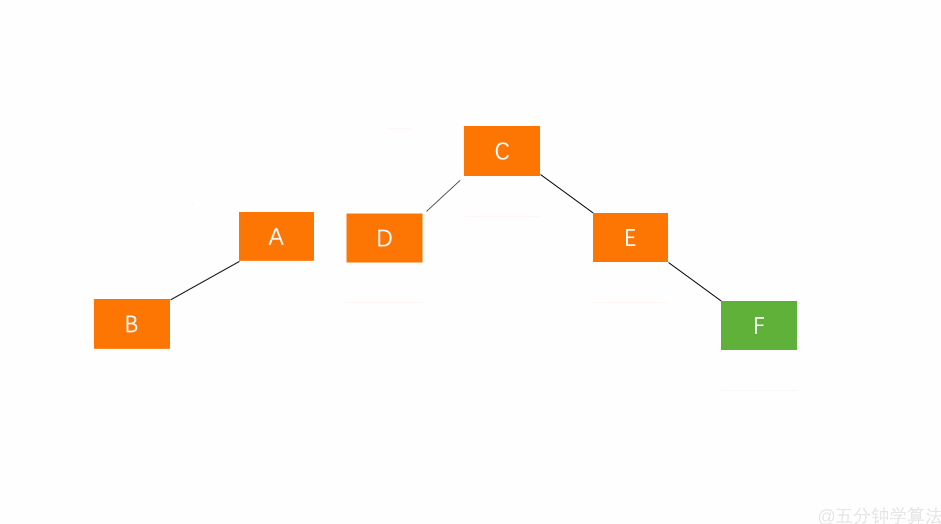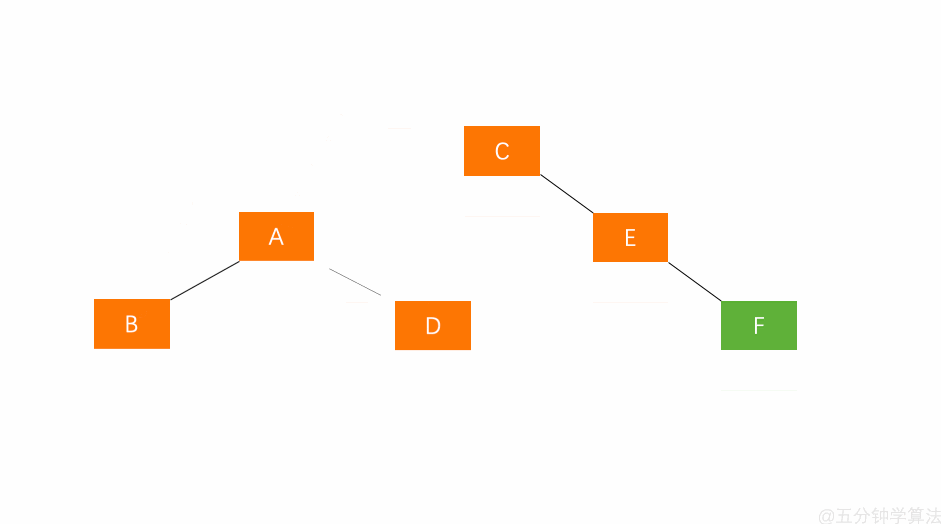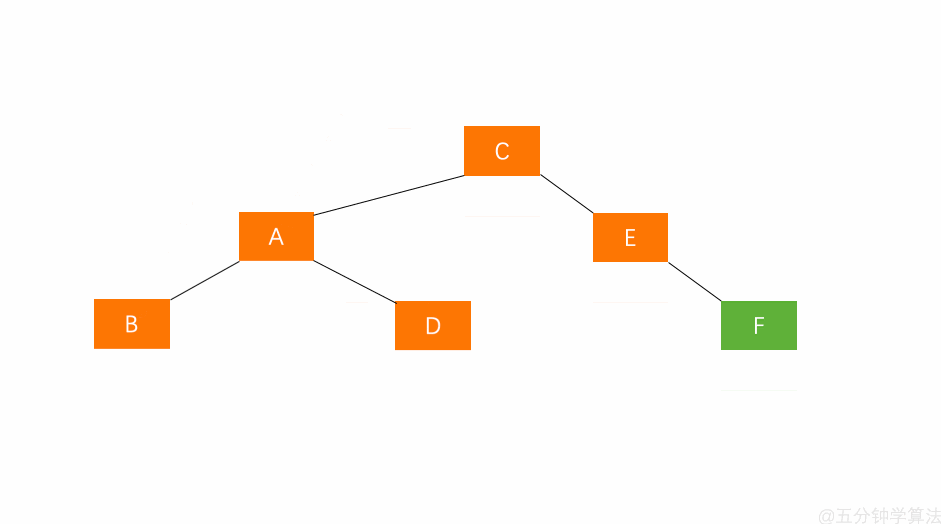
右旋步骤

1. 节点的左孩子代表此节点
2. 节点的左孩子的右子树变为节点的左子树
3. 将此节点作为左孩子节点的右子树

如图

 四种插入节点方式

一、LL | 在 A 的左子树根节点的左子树上插入节点而破坏平衡 | 右旋转 |

二、| RR | 在 A 的右子树根节点的右子树上插入节点而破坏平衡 | 左旋转 |

三、| LR | 在A的左子树根节点的右子树上插入节点而破坏平衡 | 先左旋后右旋 |

有兴趣的可以去找找对应的资料看看，在此就不展示的

四、| RL | 在 A 的右子树根节点的左子树上插入节点而破坏平衡 | 先右旋后左旋 |

 

AVL树的四种删除节点方式

一、删除叶子节点

二、删除的节点只有左子树

三、删除的节点只有右子树

四、删除的节点既有左子树又有右子树