基于MapReduce的大矩阵乘法（Spark实现）

矩阵-向量乘法实现

\[x_i=\sum_{j=1}^nm_{ij}v_{j} \]

Map函数

Map函数应用于M的一个元素，但是如果执行Map任务的计算节点还没有将v读到内存，那么首先以一个整体的方式读入v，然后v就可以被该Map任务中执行的Map函数所用。每个Map任务将整个向量v和矩阵M的一个文件块作为输入。对每个矩阵元素\(m_{ij}\)，Map任务会产生键值对\((i,m_{ij}v_{j})\)。因此，计算\(x_i\)的所有n个求和项\(m_{ij}v_j\)。

Reduce函数

Reduce函数简单地将所有与给定键i关联的值相加即得到结果\((i,x_i)\)。

向量v太大无法放入内存

把矩阵分割成多个宽度相等的垂直条，同时将向量分割成同样数目的水平条。我们的目标是使用足够的条以保证向量的每个条能够方便地放入计算节点的内存中。

矩阵-矩阵乘法

矩阵\(M\)中第\(i\)行第\(j\)列的元素记为\(m_{ij}\)，矩阵\(N\)中第\(j\)行第\(k\)列的元素记为\(n_{jk}\)，矩阵\(P=MN\)，其第\(i\)行第\(k\)列的元素记为\(p_{ik}\)，

\[p_{ik}=\sum_jm_{ij}n_{jk} \]

Map函数

对每个矩阵元素\(m_{ij}\)产生键值对\((j,(M,i,m_{ij}))\)，对每个矩阵元素\(n_{jk}\)产生键值对\((j,(N,k,n_{jk}))\)。

Reduce函数

对每个键\(j\)，对每个\((M,i,m_{ij})\)和\((N,k,n_{jk})\)，产生键值对，其中键为\((i,k)\)，值为\(m_{ij}n_{jk}\)。

Reduce函数

对每个键\((i, k)\)，计算与此键相关联的所有值的和，记为\(((i,k),v)\)

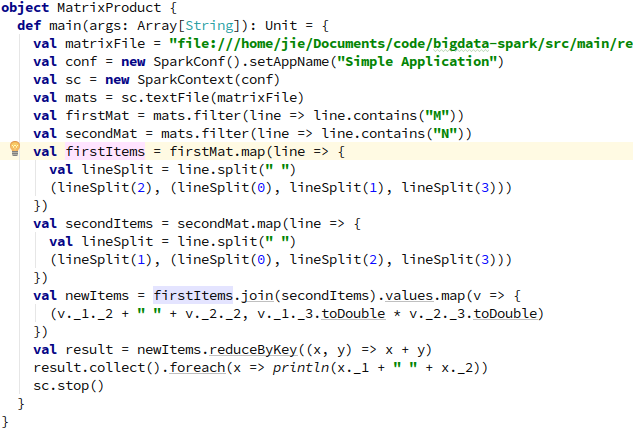
以下是使用Spark来实现上面矩阵与矩阵相乘的算法，输入是一份文件，文件的每一行为矩阵名 行号 列号 值。