使用CMSIS-DSP库进行PID控制

CMSIS-DSP是针对嵌入式系统的优化计算库，支持Cortex-M和Cortex-A内核，可以利用内核的FPU、DSP指令，提高算法的性能。这个库为我们提供了针对内核优化的向量计算、矩阵运算、数字信号处理、电机控制、统计和机器学习算法。

本文将介绍如何使用CMSIS-DSP库，在STM32单片机上，构建增量式PID控制程序。

引入CMSIS-DSP库

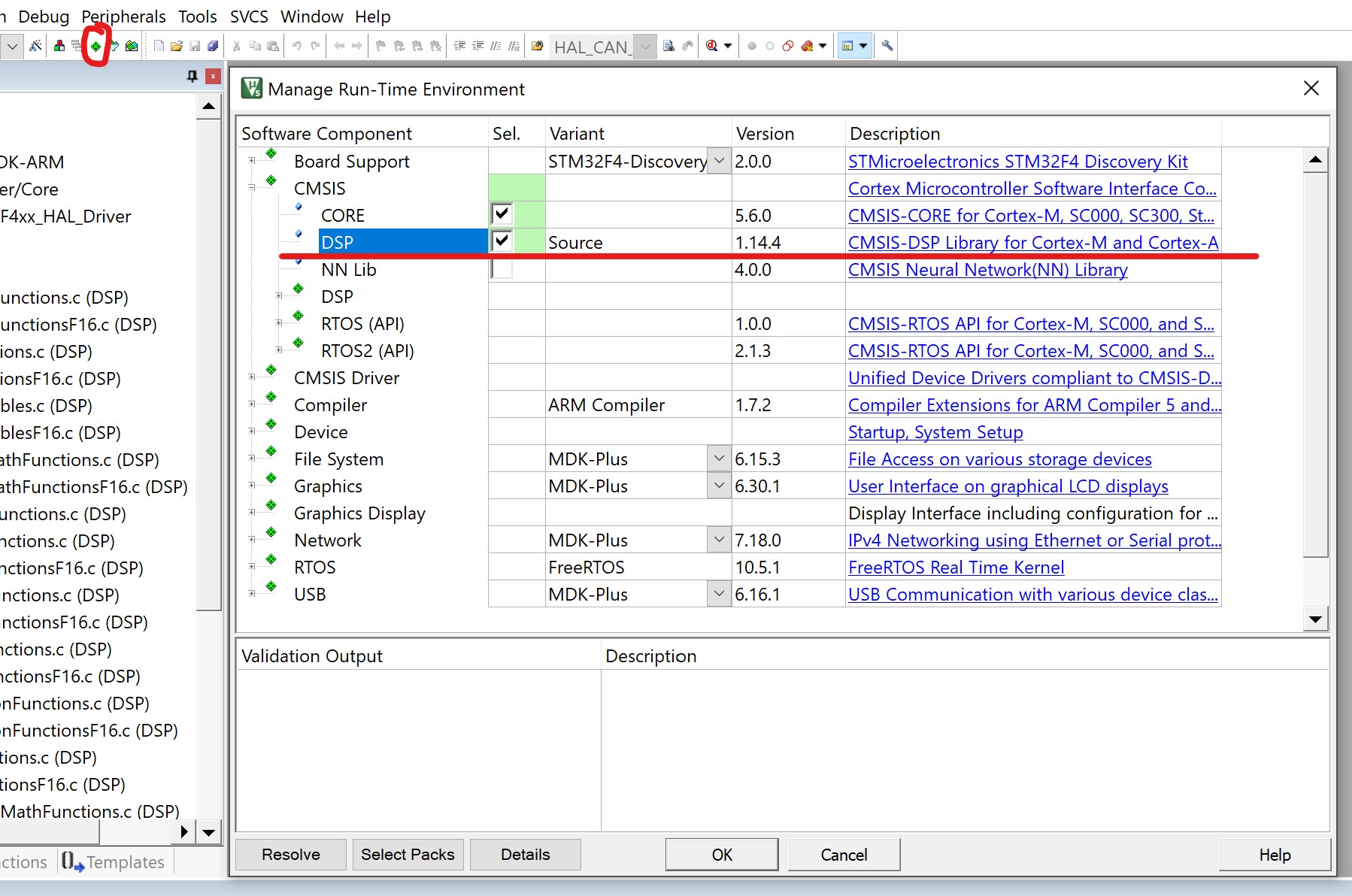
在Keil MDK-Arm中引入CMSIS-DSP库是非常方便的。建立好适用于MDK-Arm的STM32工程后，单击Manage Run-Time Environment，进入MDK-Arm提供的包管理器界面。随后，展开CMSIS，单击DSP右侧的单选框，即可完成库的导入。

MDK添加CMSIS-DSP库

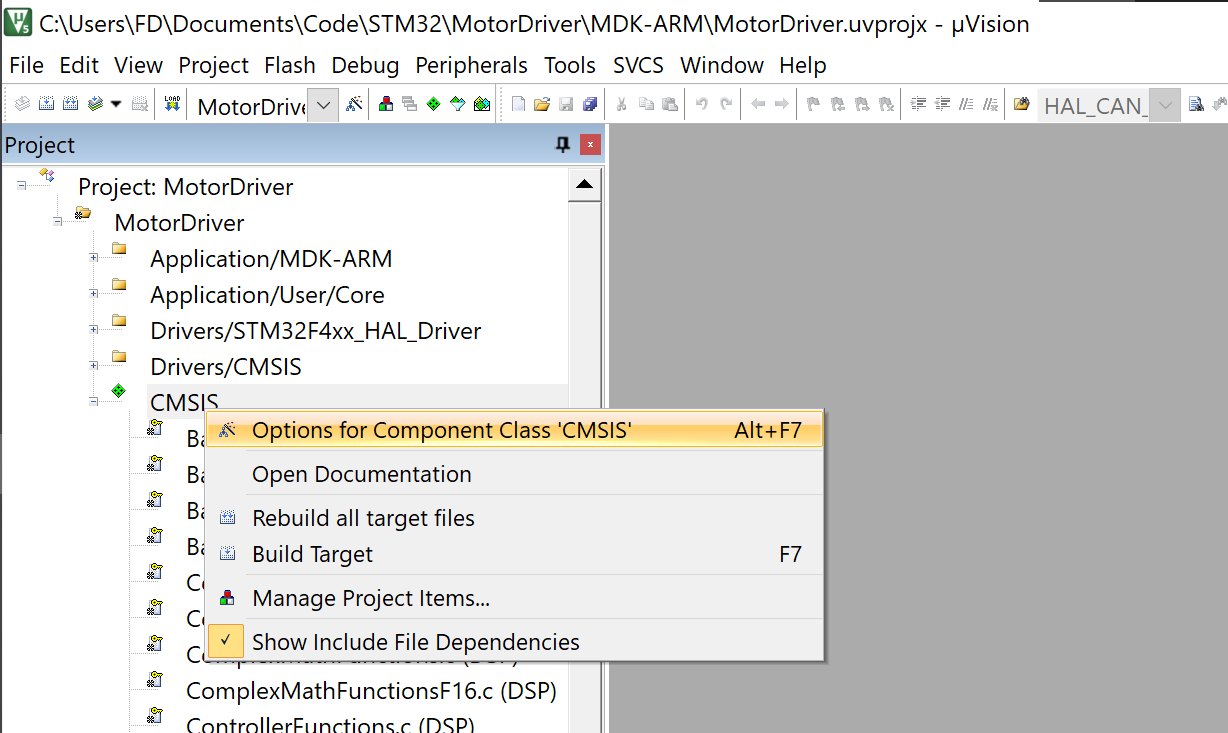
在项目管理器中，右键单击CMSIS库，选择Options for Component Class 'CMSIS'，配置DSP库的编译选项。

包含DSP库

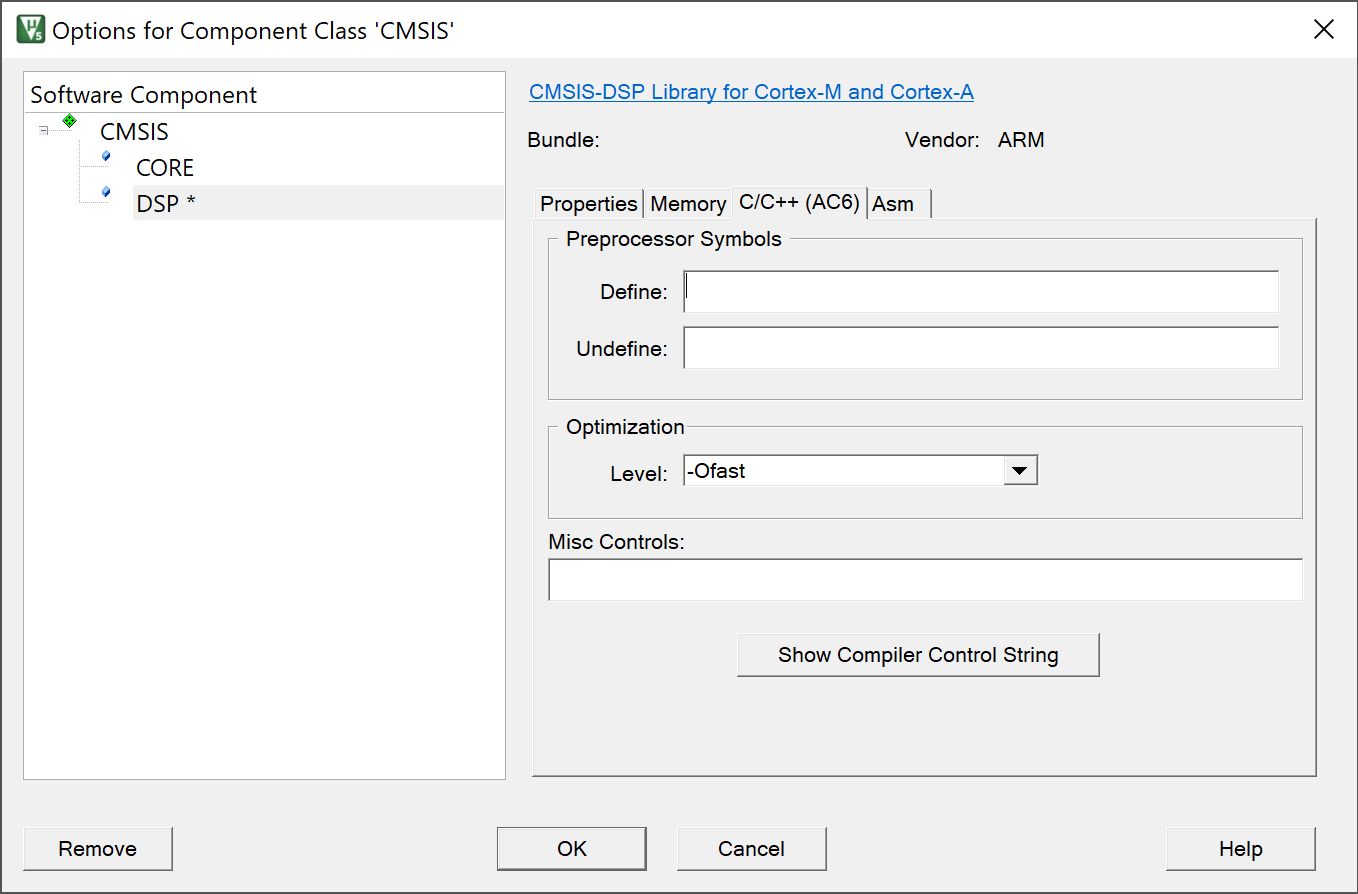
在弹出的界面中，选择DSP库的C/C++编译选项，开启-Ofast优化。

CMSIS-DSP配置

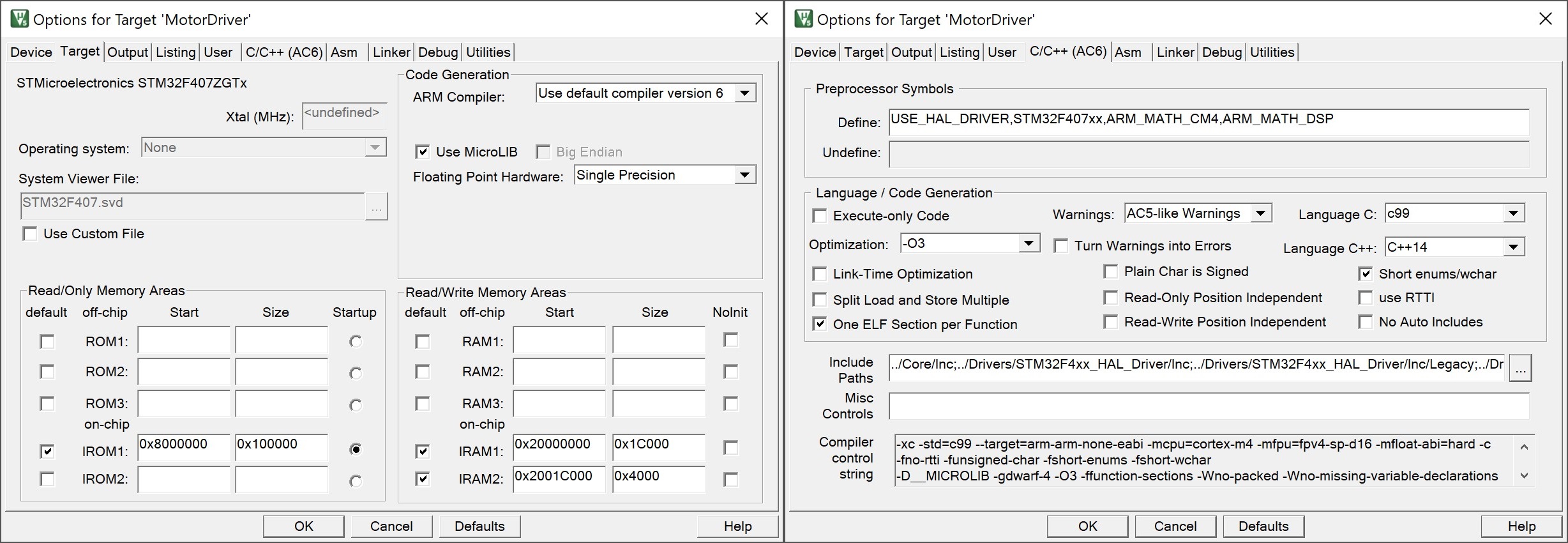
如果您的设备支持FPU，可以在工程的编译选项中，使能Floating Point Hardware并添加ARM_MATH_CM4和ARM_MATH_DSP宏，让CMSIS-DSP库能够利用硬件实现算法的加速。

编译选项

重新编译工程，若未发现错误，则说明我们已经成功引入了CMSIS-DSP库。

CMSIS-DSP提供的PID算法原理与公式推导

PID控制器（比例-积分-微分控制器），由比例单元（Proportional）、积分单元（Integral）和微分单元（Derivative）组成，是一种在工业控制应用中常见的反馈回路部件。PID控制器可以根据历史和当前的数据，来调整对系统的控制，使系统更加准确而稳定。

PID控制器的输出是关于输入量与被控量偏差的函数，是比例单元、积分单元和微分单元的线性组合，即：

$u(t) = K_pe(t) + K_i\int_{0}^{t}e(\tau)d\tau + K_i\frac{de(t)}{dt}\tag{1}$

一个完整的PID控制系统的系统框图如下所示：

PID系统框图

在本文中，我们称这个系统中的：

$y(t)$ 为被控量，表示我们需要控制的被控对象的输出量；
$r(t)$ 为输入量，是我们希望被控量在 $t$ 时刻达到的状态或目标；
$e(t)$ 为输入量与被控量之间的偏差，即： $e(t) = r(t) - y(t)$ ；
$u(t)$ 为操纵量（执行元件的输入）；
$K_p$ 、 $K_i$ 、 $K_d$ 分别是比例项、积分项和微分项的比例系数，也是我们后续进行PID参数整定所需要调整的参数。

当然，我们在使用MCU进行编程时，我们往往用的是PID控制器的离散形式，即将积分项变为累加项，微分项变为差分项，如下式所示：

$u[t] = K_pe[t] + K_i \sum_{\tau = 0}^{t}e[\tau]\Delta t + K_d\frac{e[t] - e[t - 1]}{\Delta t}\tag{2}$

式中， $\Delta t$ 为两次相邻采样的时间间隔。我们称这样的PID控制方式为位置式PID。

考虑相邻时刻，操纵量 $u[t]$ 的变化量 $\Delta u[t] = u[t] - u[t - 1]$ ，我们可以得到：

$\Delta u[t] = K_p \left(e[t] - e[t - 1]\right) + K_ie[t]\Delta t + \frac{K_d}{\Delta t} \left(e[t] - 2e[t - 1] + e[t - 2]\right)\tag{3}$

将上式化简，我们发现，PID控制器操纵量的增量，是当前时刻 $t$ 、 $t - 1$ 时刻和 $t-2$ 时刻的偏差的线性组合，即：

$\Delta u[t] = (K_p + K_i\Delta t + \frac{K_d}{\Delta t})e[t] - (K_p + \frac{2K_d}{\Delta t})e[t - 1] + \frac{K_d}{\Delta t}e[t - 2]\tag{4}$

我们称通过计算系统输入的变化量 $\Delta u[t]$ 实现PID控制的控制方式，称为增量式PID。CMSIS-DSP库中提供的PID算法，使用增量式PID的实现。在增量式PID控制器中，有：

$u[t] = u[t - 1] + \Delta u[t]\tag{5}$

在CMSIS-DSP中的PID实现中，认为 $\Delta t = 1$ （或者说假定用户已经将 $\Delta t$ 加权至 $K_i$ 和 $K_d$ 构成新的 $K_i$ 和 $K_d$ ）。那么， $u[t]$ 的变化量 $\Delta u[t]$ 可以用下面的式子如式(6)：

$\Delta u[t] = A_0e[t] + A_1 e[t - 1] + A_2e[t - 2]\tag{6}$

其中：

$A_0 = K_p + K_i + K_d\\ A_1 = -K_p - 2K_d\\ A_2 = K_d\tag{7}$

因此，在增量式PID系统中，合并式(5)和式(6)，我们可以通过式(8)计算操纵量 $u[t]$ 。这个式子，也是CMSIS-DSP库中，PID的实现原理：

$u[t] = u[t - 1] + A_0e[t] + A_1 e[t - 1] + A_2e[t - 2]\tag{8}$

对于拥有DSP的指令的芯片，在编译器强大的优化功能下，可以在一个指令周期内完成式(8)所示的乘加运算。这大大提高了PID的计算速度。

CMSIS-DSP库的PID控制接口

数据类型

CMSIS-DSP库的PID控制器，有基于三种基于不同数据类型的实现。这三种数据类型分别是q15，q31和f32，分别表示：16位有符号整数int16_t、32位有符号整数int32_t、32位浮点数float32_t。

在CMSIS-DSP库实现的PID控制器，函数和结构体的命名都是“名称+数据类型后缀”的命名方式。例如：arm_pid_instance_q15、arm_pid_instance_q31和arm_pid_instance_f32是基于不同数据类型实现的PID控制的结构体；arm_pid_q15、arm_pid_q31和arm_pid_f32是基于不同数据类型实现的计算PID增量的函数。

在接下来的文段中，我们将以f32类型为例，介绍如何使用CMSIS-DSP库的PID控制器进行PID控制，若要使用其它数据类型的PID实现，只需按照这种命名方式，换用相应数据类型的函数、结构体即可。

PID控制结构体的定义

在CMSIS-DSP中，PID的参数信息、历史误差信息，都被记录在arm_pid_instance_xxx结构体中，例如：

 /**
 * @ingroup PID
 * @brief Instance structure for the floating-point PID Control.
 */
typedef struct {
    float32_t A0;        /**< The derived gain, A0 = Kp + Ki + Kd . */
    float32_t A1;        /**< The derived gain, A1 = -Kp - 2Kd. */
    float32_t A2;        /**< The derived gain, A2 = Kd . */
    float32_t state[3];  /**< The state array of length 3. */
    float32_t Kp;        /**< The proportional gain. */
    float32_t Ki;        /**< The integral gain. */
    float32_t Kd;        /**< The derivative gain. */
} arm_pid_instance_f32;

若我们认为当前时刻为 $t$ 时刻，则结构体中各个参数的定义如下所示：

Kp、Ki和Kd需要我们自行设置，分别是比例项、积分项和微分项的比例系数 $K_p$ 、 $K_i$ 和 $K_d$ ；
A0、A1和A2分别对应式(7)中的 $A_0$ ， $A_1$ 和 $A_2$ ，其具体意义与前文所述一致；
state是PID控制的状态数组。
- state[0]表示 $t - 1$ 时刻的偏差，即 $e[t-1]$ ；
- state[1]表示 $t - 2$ 时刻的偏差，即 $e[t-2]$ ；
- state[2]表示的是前1时刻的操纵量，即 $u[t - 1]$

PID控制结构体的初始化

当我们在初始化这个结构体的时候，我们需要且只需手动对Kp、Ki和Kd这三个成员进行赋值。之后，我们需要调用arm_pid_init_xxx函数，初始化这个结构体。

arm_pid_init_xxx函数接受两个参数，第一个参数是PID控制结构体的指针，第二个参数是一个整数标志位，当它为0时，只计算A0、A1和A2的值，不初始化state数组；当它为1时，则初始将state数组，将其置为0。在编程中，如果我们首次初始化该结构体，则应当将resetStateFlag置为1；当我们非首次初始化（如PID参数整定过程中），我们需要更新Kp、Ki或Kd的值，我们可以将其置为0，以提高性能。

这个函数初始化的过程分两步：

利用Kp、Ki和Kd，通过我们先前推导的公式，计算A0、A1和A2的值。
若resetStateFlag参数为1，则将state数组置为0。

 /**
 * @brief         Initialization function for the floating-point PID Control.
 * @param[in,out] S               points to an instance of the PID structure
 * @param[in]     resetStateFlag
 *                  - value = 0: no change in state
 *                  - value = 1: reset state
 * @return        none
 */
void arm_pid_init_f32(arm_pid_instance_f32 *S, int32_t resetStateFlag) {
    /* Derived coefficient A0 */
    S->A0 = S->Kp + S->Ki + S->Kd;
    /* Derived coefficient A1 */
    S->A1 = (-S->Kp) - ((float32_t) 2.0f * S->Kd);
    /* Derived coefficient A2 */
    S->A2 = S->Kd;
    /* Check whether state needs reset or not */
    if (resetStateFlag) {
        /* Reset state to zero, The size will be always 3 samples */
        memset(S->state, 0, 3U * sizeof(float32_t));
    }
}

当我们进行PID参数整定时，需要不断地调整 $K_p$ 、 $K_i$ 和 $K_d$ 的值。我们每次调整 $K_p$ 、 $K_i$ 和 $K_d$ 的值，都应该调用这个函数，重新计算 $A_0$ 、 $A_1$ 和 $A_2$ 的值。但是此时，我们可以不重置state数组。

操纵量的更新

作为一种反馈控制算法，PID控制算法是一种按偏差进行控制的过程。由于扰动或输入量变化等因素的影响，偏差往往不恒为0；而我们的控制系统，为了达到尽量让偏差为0的目标，需要对输出量进行采样，与输入量不断地更新操纵量 $u[t]$ ，以使得被控量贴合输入量。

对于增量式PID算法，其核心步骤就在于计算操纵量的变化量 $\Delta u[t]$ ，并更新操纵量 $u[t]$ 。 $u[t]$ 的计算，可以通过arm_pid_xxx进行计算。这个函数的输入是当前时刻的偏差 $e[t]$ ，输出的是操纵量 $u[t]$ 。

值得注意的是，arm_pid_xxx函数不会对输出进行限幅，关于这一点，我们将在后续进行更深入的讨论。

 /**
 * @ingroup PID
 * @brief         Process function for the floating-point PID Control.
 * @param[in,out] S   is an instance of the floating-point PID Control structure
 * @param[in]     in  input sample to process
 * @return        processed output sample.
 */
__STATIC_FORCEINLINE float32_t arm_pid_f32(arm_pid_instance_f32 * S, float32_t in) {
    float32_t out;
 
    /* u[t] = u[t - 1] + A0 * e[t] + A1 * e[t - 1] + A2 * e[t - 2]  */
    out = (S->A0 * in) +
      (S->A1 * S->state[0]) + (S->A2 * S->state[1]) + (S->state[2]);
 
    /* Update state */
    S->state[1] = S->state[0];
    S->state[0] = in;
    S->state[2] = out;
 
    /* return to application */
    return (out);
}

状态的清除

在arm_pid_xxx函数中，是否清空状态数组state取决于我们输入的参数。当我们未修改Kp、Ki或Kd的值，不需要重新更新A0、A1和A2的值时，若我们要清空状态数组state时，可以使用arm_pid_reset_xxx函数。

 /**
 * @brief         Reset function for the floating-point PID Control.
 * @param[in,out] S  points to an instance of the floating-point PID structure
 * @return        none
 * @par           Details
 *                The function resets the state buffer to zeros.
 */
void arm_pid_reset_f32(arm_pid_instance_f32 *S) {
    /* Reset state to zero, The size will be always 3 samples */
    memset(S->state, 0, 3U * sizeof(float32_t));
}

PID控制的实现

基础控制

根据上面的介绍，我们使用PID进行积分控制的方法，也就呼之欲出了。其伪代码如下所示：

 void pid_control(float Kp, float Ki, float Kp, float delta_t) {
    // 在CMSIS-DSP中的PID实现中，认为Δt = 1，
    // 故需要调整Kp和Ki的值，保证系统在采样率变化时的鲁棒性
	arm_pid_instance_f32 controller = {
        .Kp = Kp,
        .Ki = Ki * delta_t,    
        .Kd = Kd / delta_t 
    };
    arm_pid_init_f32(&controller, 1);       // 初始化结构体，要记得清空state数组
    while (1) {
        const float r = get_reference();    // 读取当前系统的输入量
        const float y = get_status();       // 读取当前的被控量
        const float error = r - y;          // 计算偏差
        const float u = arm_pid_f32(&controller, error);    // 计算PID的操纵量
        execute(u);        // 使用最新的操纵量，调整执行元件，实现控制
        delay(delta_t);    // 实际可以使用定时器等机制，实现循环体中语句的定期执行
    }
}

输出限幅的控制

在实际工程中，受硬件条件的限制，操纵量往往是有一定范围的。如矩形波占空比的大小，只能是0~100%；输出电压的大小，不会超过系统中的最高电压；电流的大小，也不会越过欧姆定律的限制……

但是，CMSIS-DSP库的PID实现，为了追求极致的效率，未将这一点纳入考量。当我们在这样的控制系统中应用上面的控制程序，就有可能出现 $u[t]$ 趋向于无穷的情况。此时，当PID控制器的输入量发生变化，PID控制器可能不会及时的响应。这时，我们要人为地限定操纵量的大小，使其符合工程实际。我们称这样的操作为“输出限幅”。

使用CMSIS-DSP库实现PID，当我们需要进行输出限幅地时候，需要修改stete数组的第三个成员——记录着上一时刻操纵量的 $u[t-1]$ 的state[2]成员，保证其在合理的范围内，避免超出工程实际的幅值。具体实现如下所示：

 void pid_control(float Kp, float Ki, float Kp, float delta_t) {
    // 在CMSIS-DSP中的PID实现中，认为Δt = 1，
    // 故需要调整Kp和Ki的值，保证系统在采样率变化时的鲁棒性
	arm_pid_instance_f32 controller = {
        .Kp = Kp,
        .Ki = Ki * delta_t,    
        .Kd = Kd / delta_t 
    };
    arm_pid_init_f32(&controller, 1);       // 初始化结构体，要记得清空state数组
    while (1) {
        const float r = get_reference();    // 读取当前系统的输入量
        const float y = get_status();       // 读取当前的被控量
        const float error = r - y;          // 计算偏差
        arm_pid_f32(&controller, error);    // 计算PID的操纵量
        // 进行输出限幅
        if (controller.state[2] > OUTPUT_MAX) {
            controller.state[2] = OUTPUT_MAX;
        } else if (controller.state[2] < OUTPUT_MIN) {
            controller.state[2] = OUTPUT_MIN;
        }
        // 完成输出限幅，用限幅后的操纵量控制系统
        execute(controller.state[2]);   // 使用最新的操纵量，调整执行元件，实现控制
        delay(delta_t);      // 实际可以使用定时器等机制，实现循环体中语句的定期执行
    }
}

总结

关于使用CMSIS-DSP库实现PID控制，无论是中外的互联网上，资料都很少。官方文档目前仍没有提供例程。但是当我们理解了增量式PID的计算公式后，再来看CMSIS-DSP库的PID控制接口，实际上它是非常简单，甚至是简陋的。这也是为什么我以解读源码的方式，写下这篇文章。

CMSIS-DSP库的PID控制接口，其优化思路，主要还是在于写出利于编译器优化的代码（如将复杂的PID计算过程，转换为式(8)所示的乘加运算），借助现代编译器强大的优化功能，提高代码的性能。此外，对于被反复调用的arm_pid_xxx函数，这个库也使用了__STATIC_FORCEINLINE，强制编译器进行内联。这些优化技巧，是值得我们学习的。

参考文献

posted @ 2023-06-03 14:17 fang-d 阅读(4065) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

一方天地

给技术一方自由的天地