DS博客作业06--图
1.本周学习总结
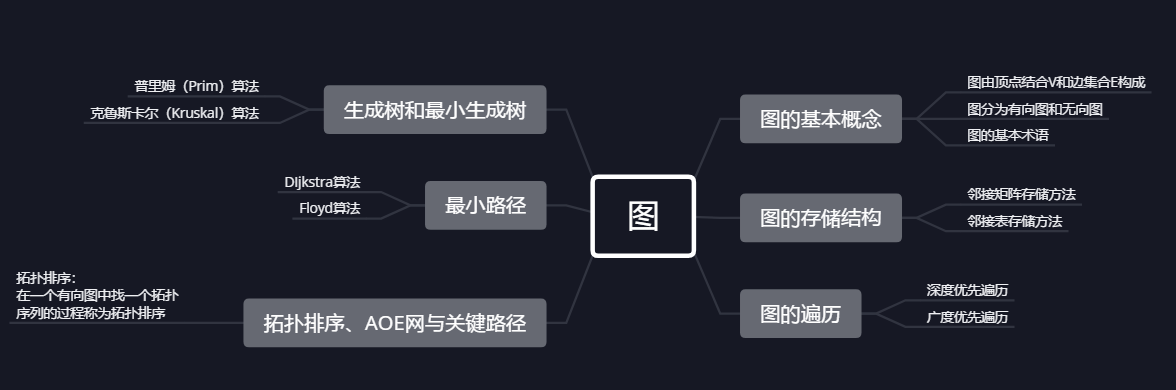
1.思维导图
2.谈谈你对图结构的认识及学习体会。
本次对图结构以及图结构的应用进行了学习。首先是图的一些基本知识,包含了图的概念、图的基本术语、图的存储方式以及图的遍历方式。其中图的存储方法有两种,一种是邻接矩阵存储方法,另一种是邻接表存储方法。邻接矩阵存储方法,本质上就是二维数组,利用邻接矩阵的图操作,带来一种当初学习二维数组的熟悉感。邻接表结合了数组和链表,第一次这样用,但本质上的联系依旧比较简单。图结构的重点应该还是放在后期学习的一些算法上。图遍历的两种方式--深度优先遍历和广度优先遍历,是对递归或者队列的结合。个人认为图结构的重点还是在后期学习的一些解决图的最小生成树问题、图的最小路径问题、图的拓扑排序序列问题的算法。解决最小生成树问题的普里姆(Prim)和克鲁斯卡尔(Kruskal)算法,解决图最小路径问题的的Dijstra算法以及Floyd算法以及解决拓扑排序问题时栈与图的结合操作。
2.PTA实验作业
2.1.题目1:题目名称:7-1 图着色问题 (25 分)
图着色问题是一个著名的NP完全问题。给定无向图G=(V,E),问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。输入在第一行给出3个整数V(0<V≤500)、E(≥0)和K(0<K≤V),分别是无向图的顶点数、边数、以及颜色数。顶点和颜色都从1到V编号。随后E行,每行给出一条边的两个端点的编号。在图的信息给出之后,给出了一个正整数N(≤20),是待检查的颜色分配方案的个数。随后N行,每行顺次给出V个顶点的颜色(第i个数字表示第i个顶点的颜色),数字间以空格分隔。题目保证给定的无向图是合法的(即不存在自回路和重边)。对每种颜色分配方案,如果是图着色问题的一个解则输出Yes,否则输出No,每句占一行。
2.1.1设计思路
/*采用邻接表存储方法*/
typedef struct ANode
{
int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{
Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{
AdjList adjlist; //邻接表
int n, e; //图中顶点数n和边数e
} AdjGraph;
/*main函数*/
定义color存储颜色个数
n为顶点数,e为边数
建邻接表
输入v
数组a存放颜色
for k=0 to v
定义空字符串c
flag=0 /*决定输出*/
cnt=0 /*计数*/
for循环初始化visited数组
/*判断*/
for j=0 to n
输入a[j]
if 在字符串中str找不到 then
添加到c中
end if
if 颜色数超过 then
输出No
else
调用ifOK函数
end if
end for
end for
/*ifOK函数*/
指针p=NULL
flag=1
for i=0 to G->n
p指向头指针
while p
if 重色 then
输出No
end if
p往下指
end while
end for
if flag=1 then
输出Yes
end if
2.1.2代码截图


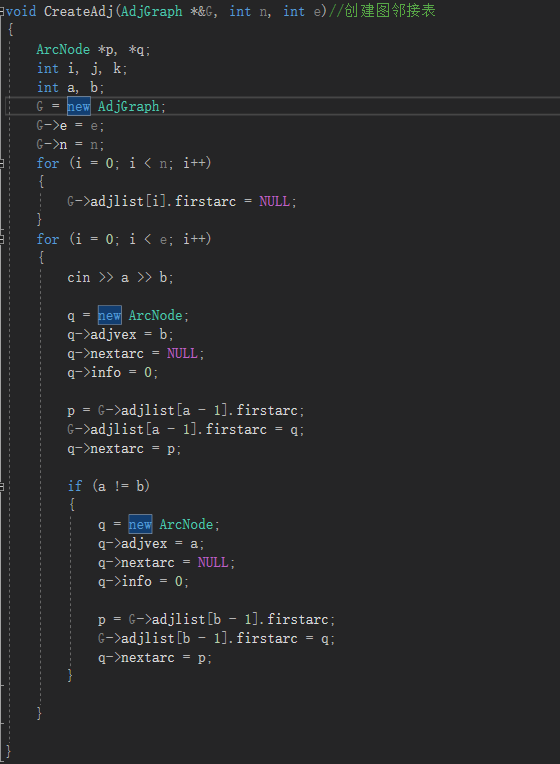
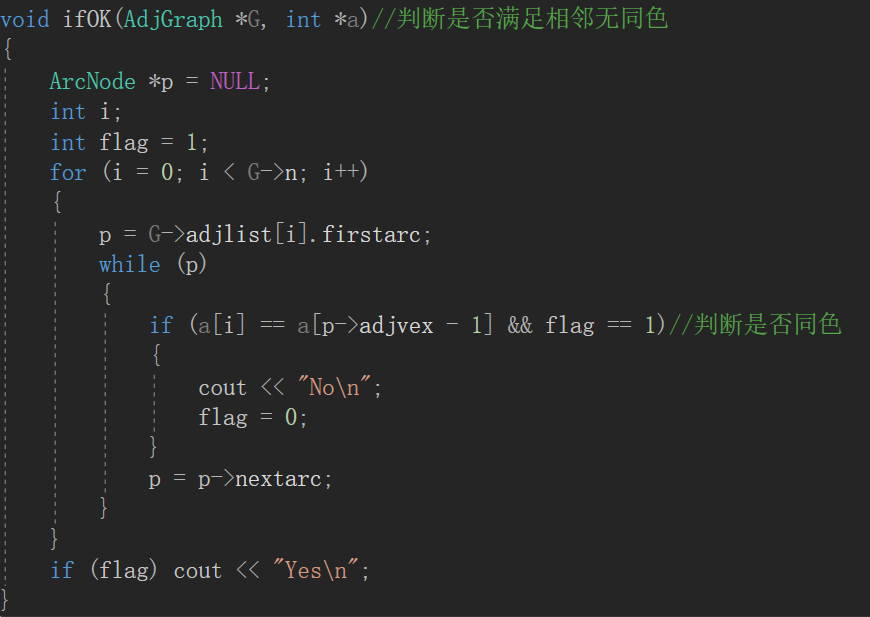
2.1.3本题PTA提交列表说明。
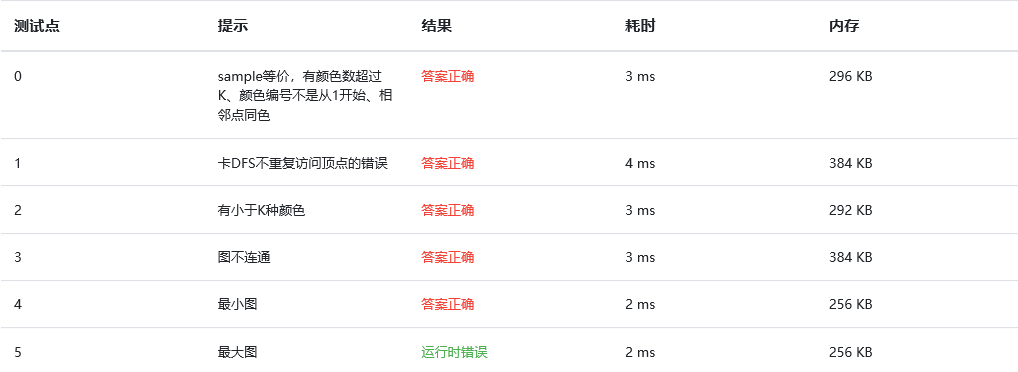

- Q:缺少直接结束的条件,会一直遍历邻接表停不下来。后来加上了判断直接结束的条件,即当visited数组全为1时结束循环,结束操作。
2.2 题目2:7-3 六度空间 (30 分)
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”“六度空间”理论虽然得到广泛的认同,并且正在得到越来越多的应用。但是数十年来,试图验证这个理论始终是许多社会学家努力追求的目标。然而由于历史的原因,这样的研究具有太大的局限性和困难。随着当代人的联络主要依赖于电话、短信、微信以及因特网上即时通信等工具,能够体现社交网络关系的一手数据已经逐渐使得“六度空间”理论的验证成为可能。假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
2.2.1设计思路
/*用到了队列queue与广度遍历的思想,采用邻接矩阵的存储方法*/
/*main函数*/
n存储顶点数,e存储边数
邻接矩阵(图)初始化
for i=0 to n
强转n为double类型,用m存储
n接收SixBfs函数的返回值,其中SixBfs函数接受参数i的值
按格式输出
end for
/*SixBfs函数*/
接受传参值存储到v
定义队列qu存储依次顶点达成广度遍历的效果
定义并初始化visited数组,用于判断顶点是都已经判断过
定义变量last存放当前层的最后一个顶点(整个过程更新5次)
定义tail存放与当前结点相连的最后一个顶点
while qu不为空
出队到v
for i=0 to n
if该边存在并且未曾走过 then
count++
边的另一个顶点入队
visited标记为走过
tail记录为i
end if
if last==v then/*当前结点的所有相邻可能已经全部判断完毕*/
level++
last=tail /*更新last*/
end if
if level==v
break
end if
end while
return count
2.2.2代码截图
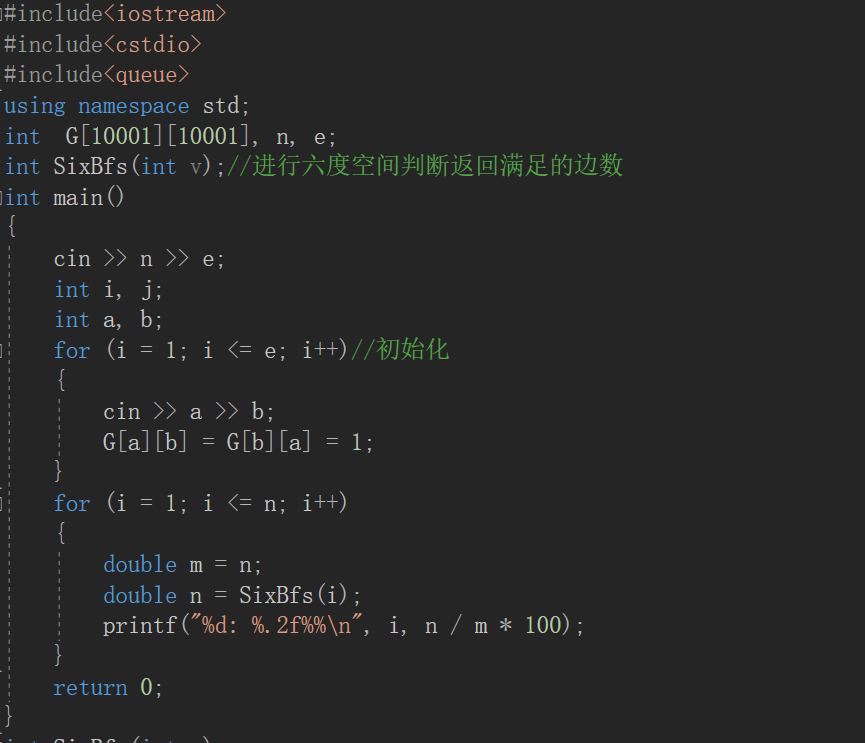
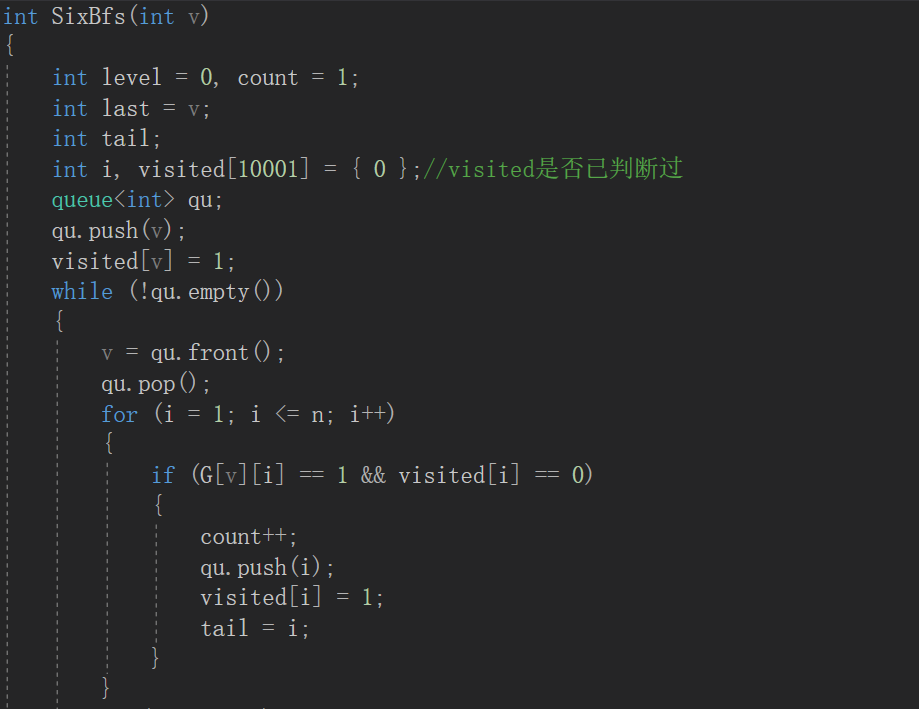

2.2.3本题PTA提交列表。

2.3 题目3:7-7 旅游规划 (25 分)
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
2.3.1设计思路
/*采用Dijkstra算法*/
全局二维数组:邻接矩阵G、每条路耗费C、判断标记vis
数组:、距离dis、耗费cost
/*main函数*/
n是城市的个数,m是高速公路的条数,s是出发地的城市编号,d是目的地的城市编号
初始化G和C
x为城市1,y为城市2,l为距离,c为耗费
循环输入建图、C矩阵
调用Dijstra函数
输出结果
/*Dijkstra函数*/
初始化vis数组和cost数组
其中注意自身的距离和费用均为0
for i=0 to n
定义x存储下标,m存储最小距离
循环找到到未走过的城市的最小距离
标记到的城市以及经过改变vis数组
此时已经找到要去的城市x以及距离m
for y=0 to n
if 某城市到x城市的距离大于m then
dis采用x到y的值
修改cost
else if 距离相等耗费少 then
采用耗费少的
修改cost
end if
end for
end for
2.3.2代码截图

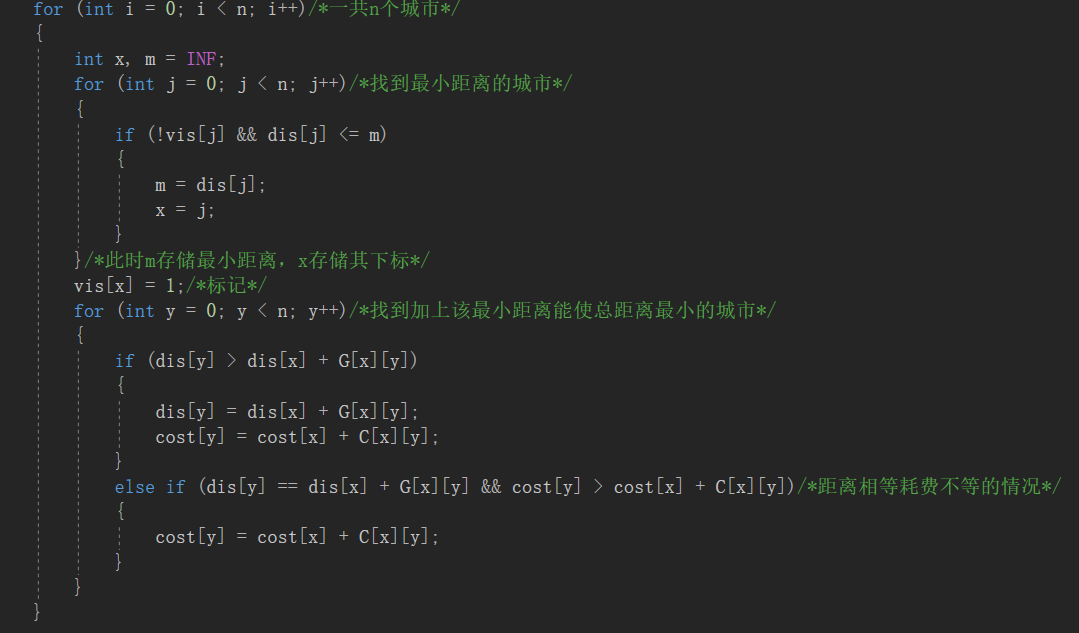
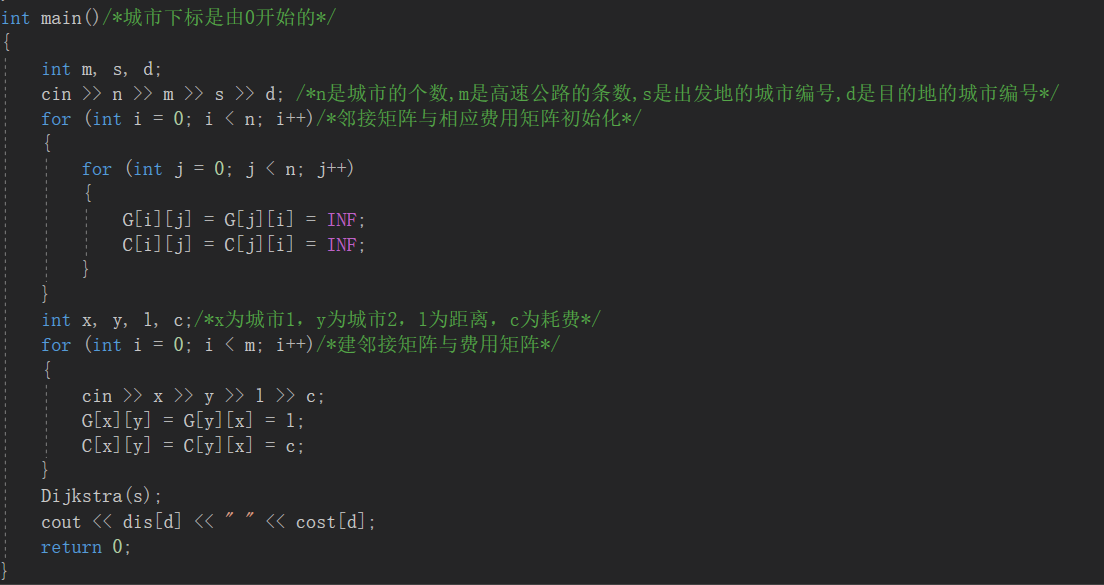
2.3.3本题PTA提交列表说明。

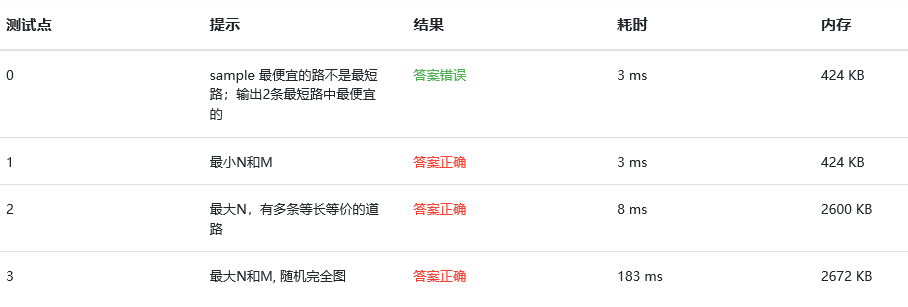
- Q1:第一个问题是输出格式错了,打的时候多加了一个空格,调试终端框里没看出来......
- Q2:没有考虑到当距离相同时费用不同的情况,考虑不全面。修改的时候还改错了一次,把高费用的输出了...后来总算改对了。
3、上机考试错题及处理办法
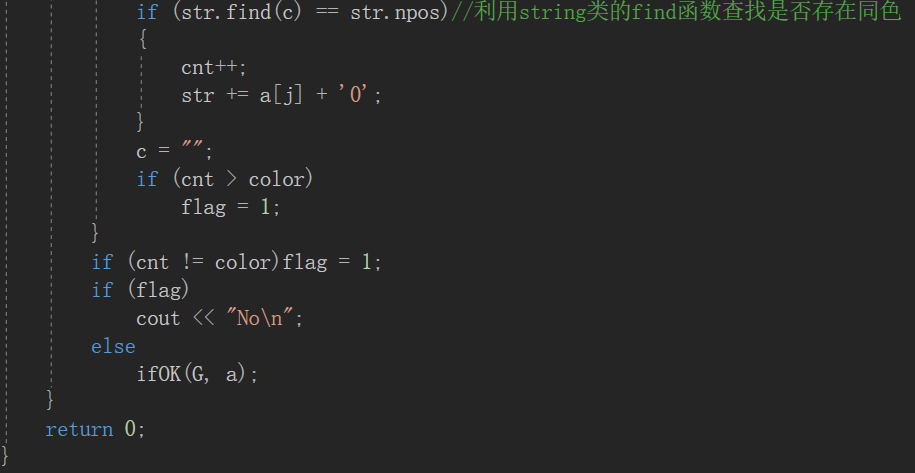
3.1.截图错题代码
题目:7-2 公路村村通 (30 分)
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。输入格式:输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。输出格式:输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
截图:
3.2 错的原因及处理方法
Q:漏了注释掉的那一部分.....没有初始化,然后程序就崩掉(跑不起来),时间来不及了,然后bug没看出来,只能cout一下了。