DS博客作业05--树

1.本周学习总结

1思维导图

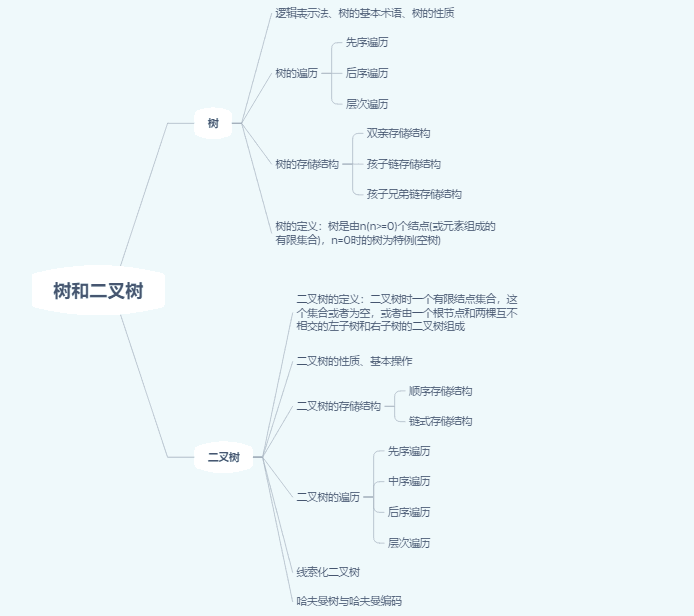
2.谈谈你对树结构的认识及学习体会。

本章学习了树与二叉树的相关知识。相对于之前所学的所有知识来说，树与二叉树的难度要高于之前所学的知识。单单从建树方面来说，就需要对树的而结构有很清晰的思路，并且对于递归的使用要嗯熟练。再有就是树的遍历，对于二叉树来说，遍历的方法有先序遍历、中序遍历、后序遍历与层次遍历四种方法，在这当中，先序遍历、中序遍历、后序遍历的序列还可以相互转换，不过需要对三种遍历的过程很熟练。层次遍历利用到了之前用到的队列的知识点。就存储结构而言，树的存储结构还是分为顺序存储结构与链式存储结构，这点与之前所学的栈与对列很是相似。

2.PTA实验作业

2.1.题目1：6-4 jmu-ds-表达式树 (25 分)

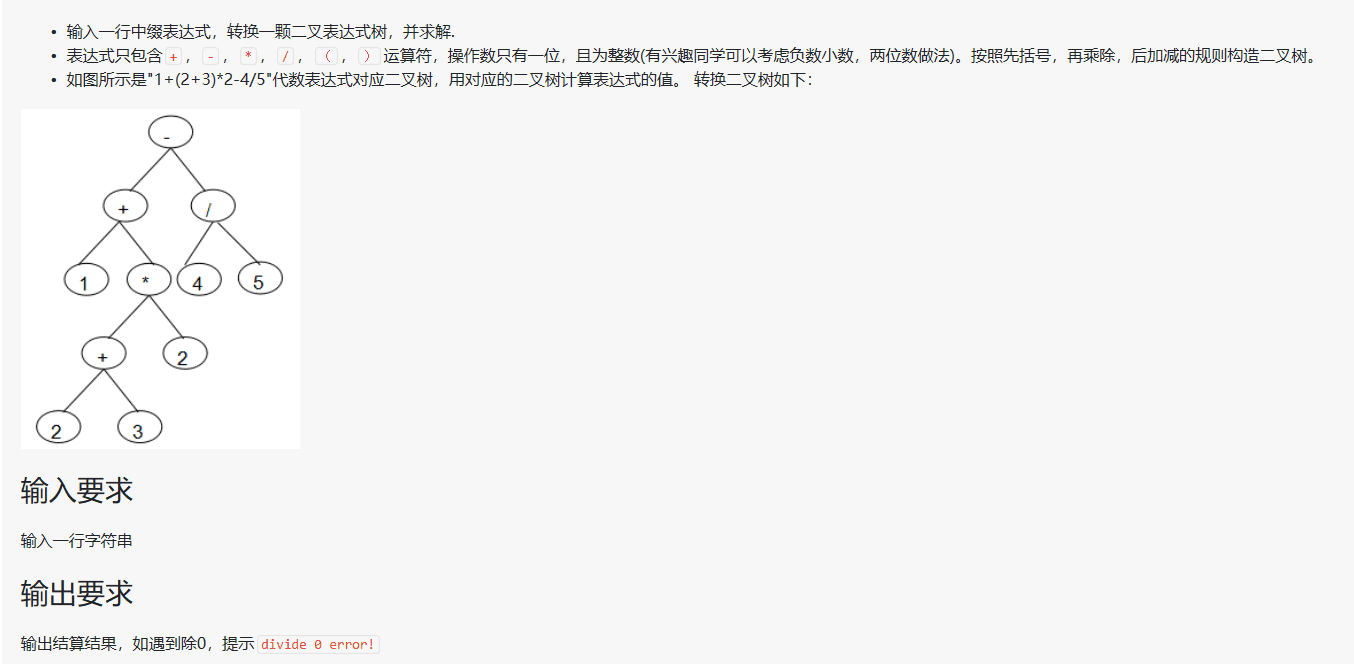
2.1.1设计思路

/*自己的方法比较直接，也比较复杂，听说别人只要几十行就能搞定这一题了QAQ*/
/*先将中缀表达式转换为后缀表达式*/
定义栈ope存放运算符 定义字符数组newstr存放后缀表达式 i为下标
字符c为str[i]
while c不为'\0'
    if c是数字 then
        直接入newstr字符数组
   else if c是右括号 then
        出栈到newstr字符数组至栈顶为左括号
    else if 是左括号
        全部入栈直至右括号
    else
        if 优先级大于栈顶 then
            全部出栈后入栈
        else
            入栈
        end if
    end if
end while
/*得到后缀表达式newstr*/
/*递归建树*/
定义树结点栈BT和数字字符栈num
i为下标 
while遍历后缀表达式
    if当前为数字 then
        入数字栈num
    else if当前树节点栈恰好有两个操作数 then
        建立一颗子树
        子树根入栈
    else if
        当前为操作符且数字栈数字大于两个
        建立一个树节点并入BT栈
    end if
end while
/*计算表达式树*/
定义result为记录当前树的结果
if 此时结点T为空 递归到此结束返回
else 
    if 此时为叶子节点 then 
        返回叶子节点的数值
    else if 此时为操作符号 
        根据操作符递归返回其左右孩子的结果
    end if
end if 

2.1.2代码截图

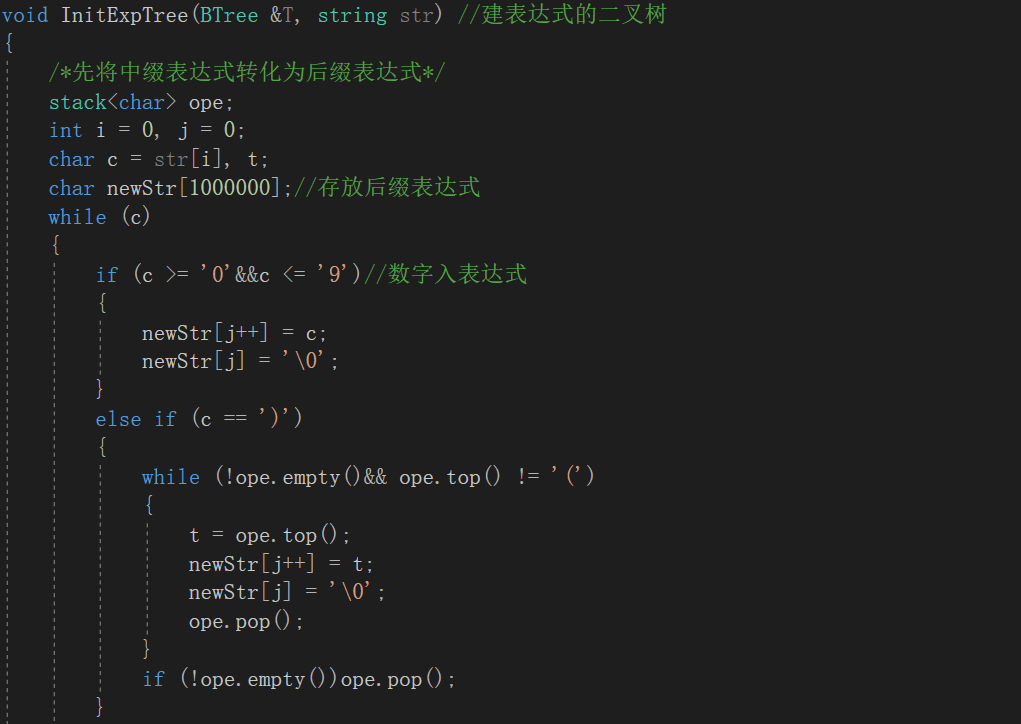
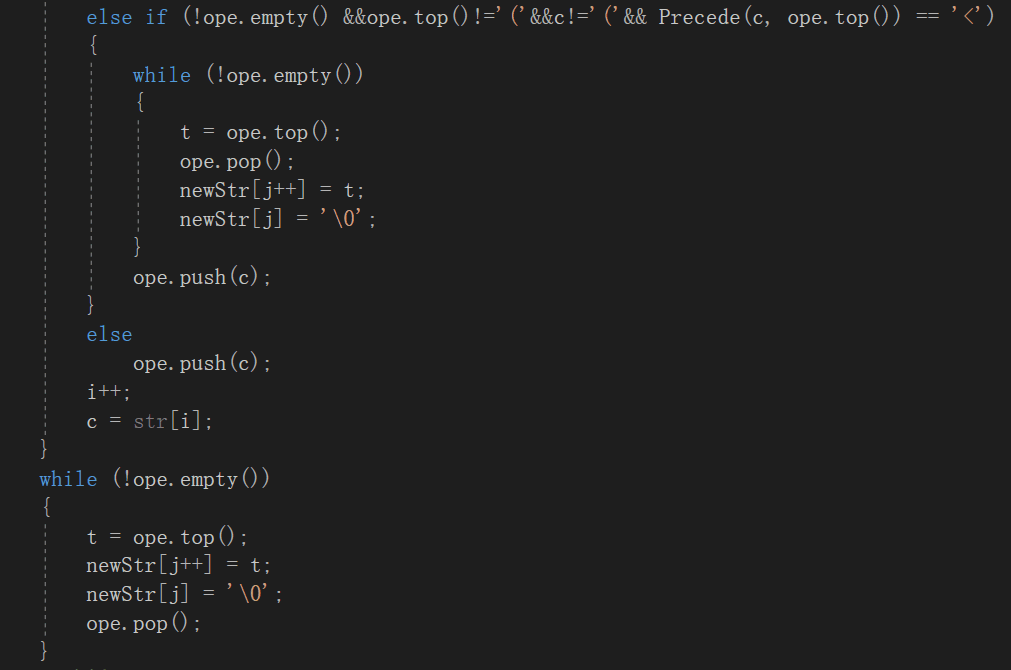
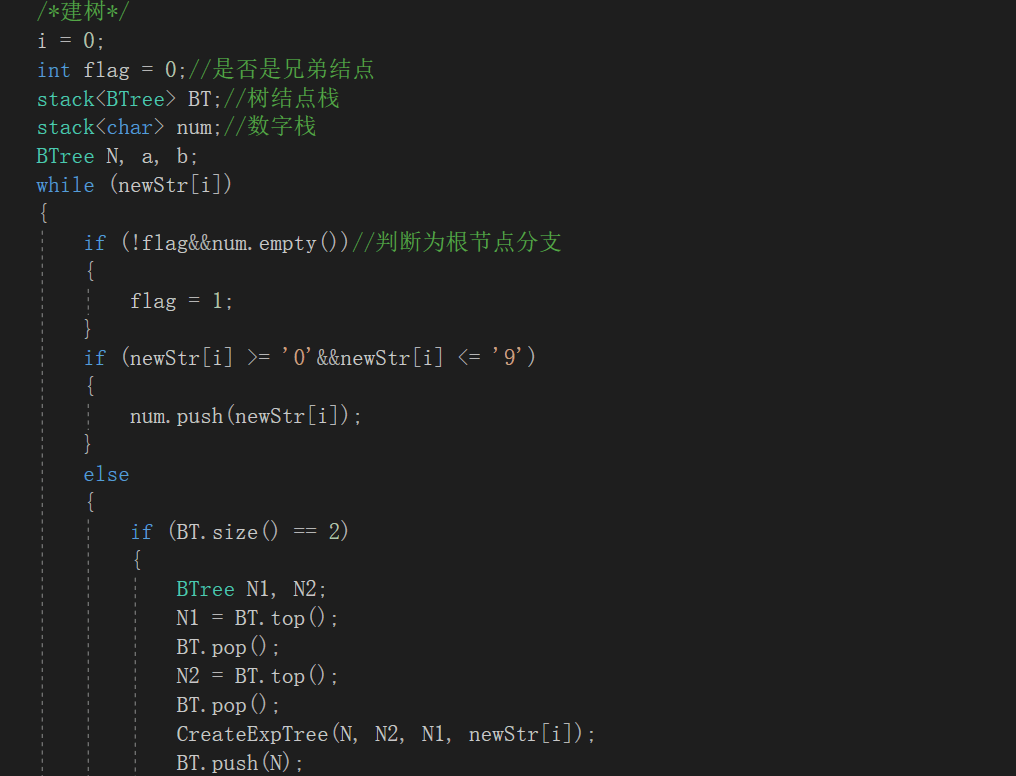
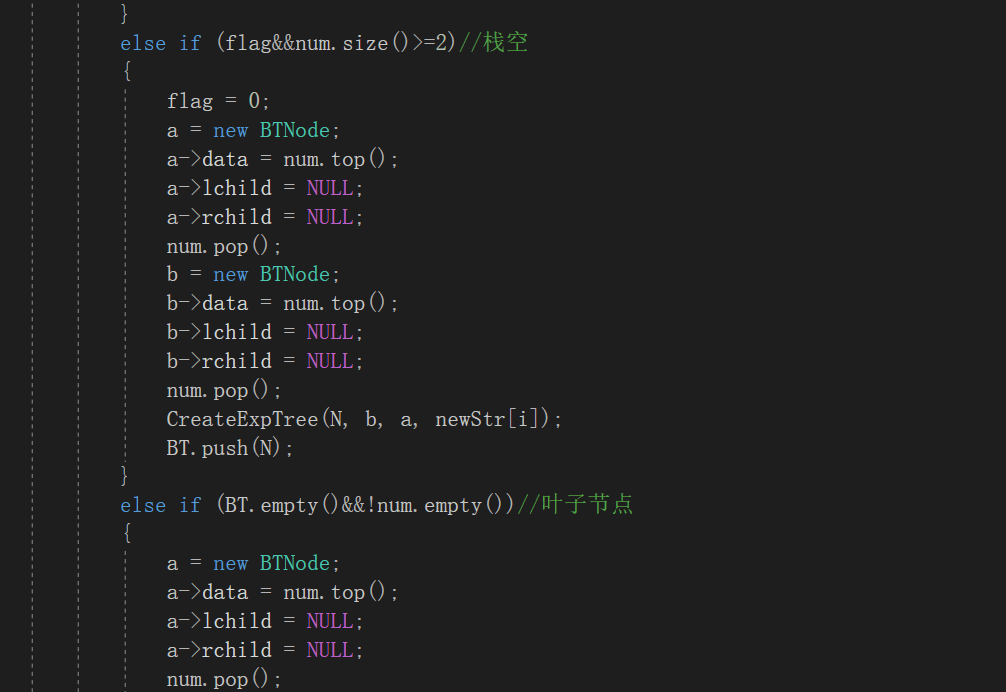
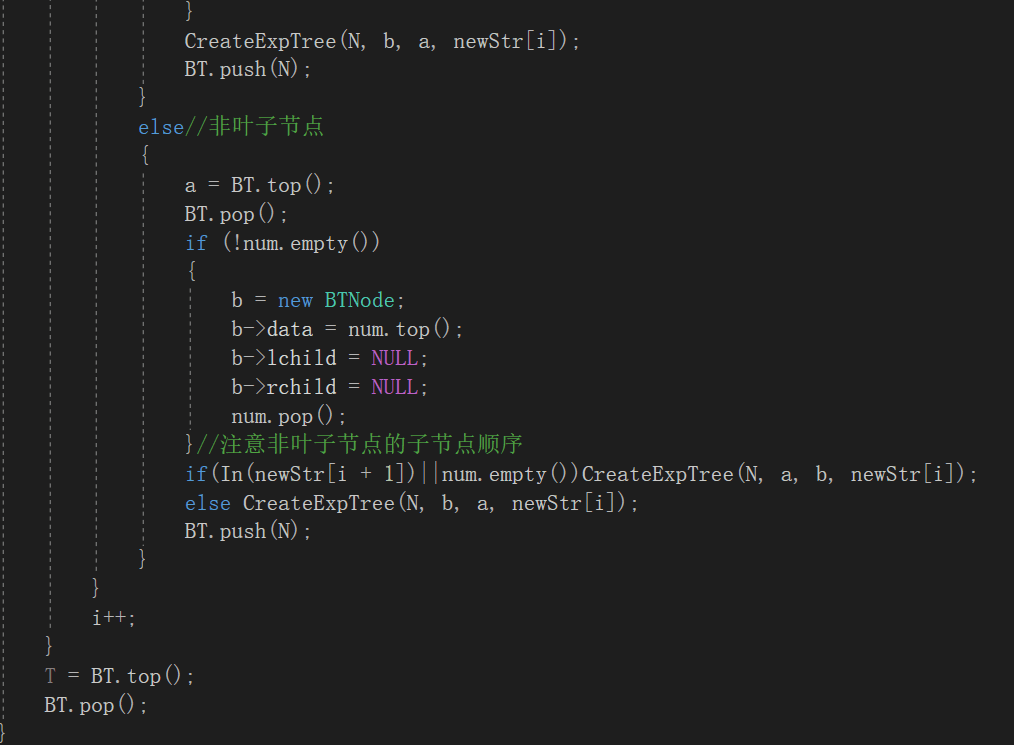
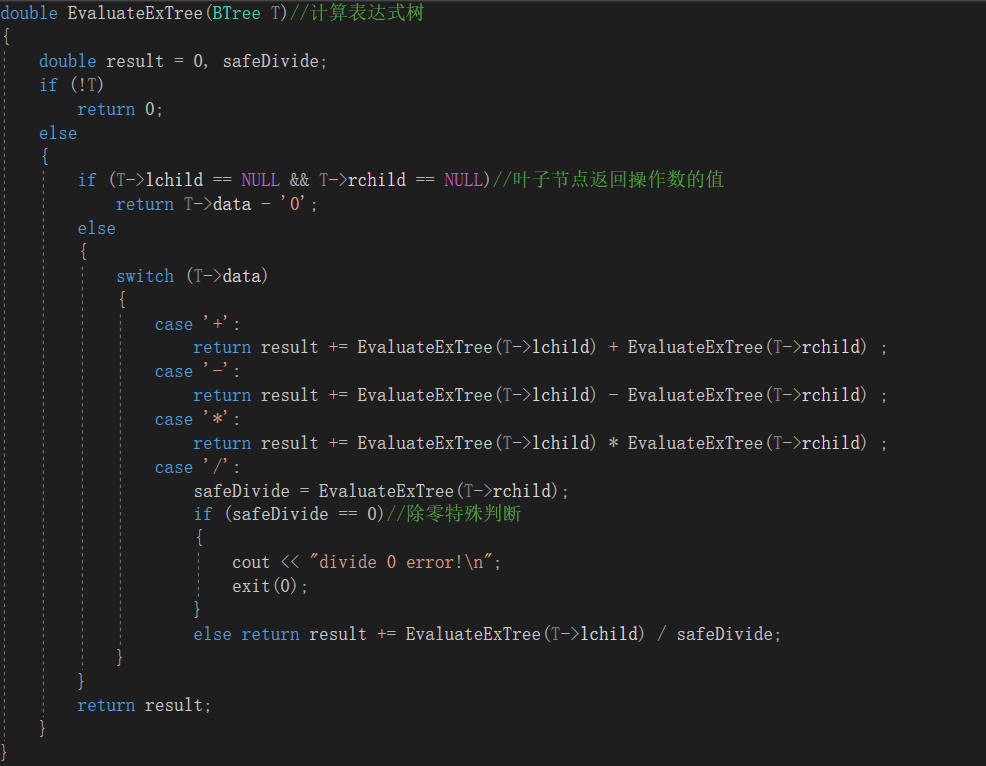
2.1.3本题PTA提交列表说明。

• 问题1及其调试过程、解决方法
  问题1话还是比较严重的，树结构的建立过程混乱了，树部分分支情况不统一，导致用同样计算函数来算会出错。在经过pta题目自带的测试数据没有问题后，还是出现了bug。我测试了题目自带的表达式"1+(2+3)2-4/5"，发现输出的并不是结果10.2，而是9.75，我发现了问题，再做除法时的左右叶子节点顺序错了。我调整完顺序之后，又自己搞了两组数据“0-1”和“00-1”，这两组数据的答案应该都是-1才对，然而实际上我的输出，一个为-1，一个竟然是1。在再一次检查中序转后序的代码没有问题之后，我意识到，我建的树存在很大的问题。我再次使用表达式"1+(2+3)*2-4/5"结合利用vs可以查看树结点层次关系的特性，查看了我建的树（如图一），并与题目要求的树（如图二）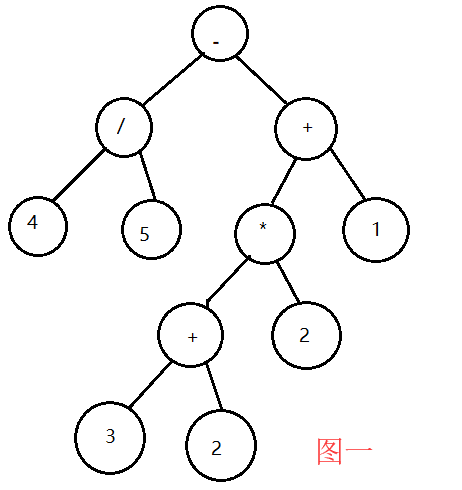
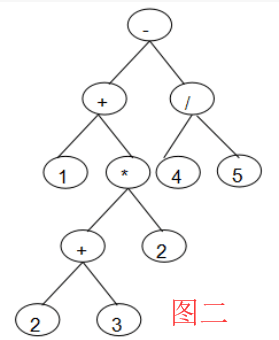
  问题的解决方法：我重新梳理了下建树的过程，发现在有些条件下，树结点的左右孩子应该是需要仔细琢磨的，如在建立非叶子结点时，就应该讨论，才不会出错。又或者是建立当前BT栈顶的结点的兄弟结点时，应该先判断一下先后关系（结合自己的计算函数，因人而异）。

• 问题2及其调试过程、解决方法
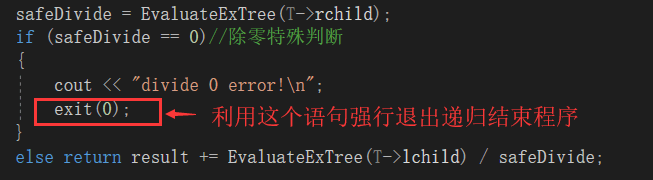
  问题在于除零问题没有处理好，题目要求提示"divide 0 error!"，我只是在出现除零的情况下输出这一句，而实际上递归并没有结束，即在提示除零错误后还会输出一个错误答案，如图：
  解决方法如图：
  

2.2 题目2：7-4 jmu-ds-二叉树叶子结点带权路径长度和 (25 分)

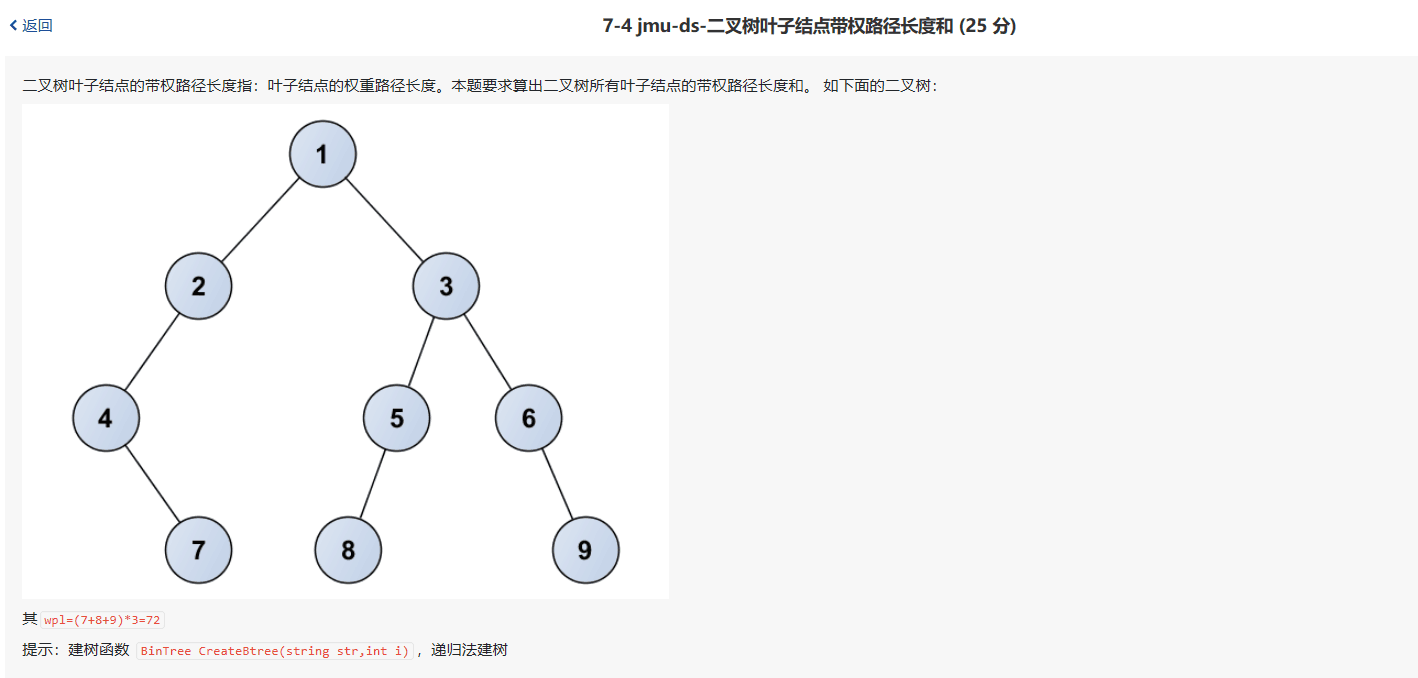
2.2.1设计思路

/*这一题采用的是我最早的思路,和老师所说的唯一区别在于,我在数的每个结点中增加了一个level,记录当前层数,所以在后来计算wpl的计算函数中,直接递归就行了*/
BinTree CreateBtree(string str, int i)//递归建树
str存储输入的字符串,i为字符位置
为btNode申请空间,btNode->data存入i位置的字符,计算并存入btNode->level
if 有左子树 then 
    递归
else
    bt->left=NULL
end if
if 有右子树 then 
    递归
else
    bt->right=NULL
end if
返回btNode

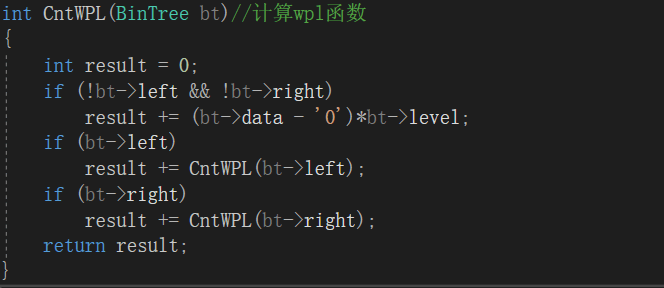
int CntWPL(BinTree bt)//计算wpl函数
定义整形变量result初始化为0,记录当前wpl值
if 为叶子节点 then
    result += 当前data-'0'的值与level之积
end if
if 有左子树
    递归
end if
if 有右子树
    递归
end if
返回result值

2.2.2代码截图

2.2.3本题PTA提交列表说明。

2.3 题目3：7-6 修理牧场 (25 分)

2.3.1设计思路

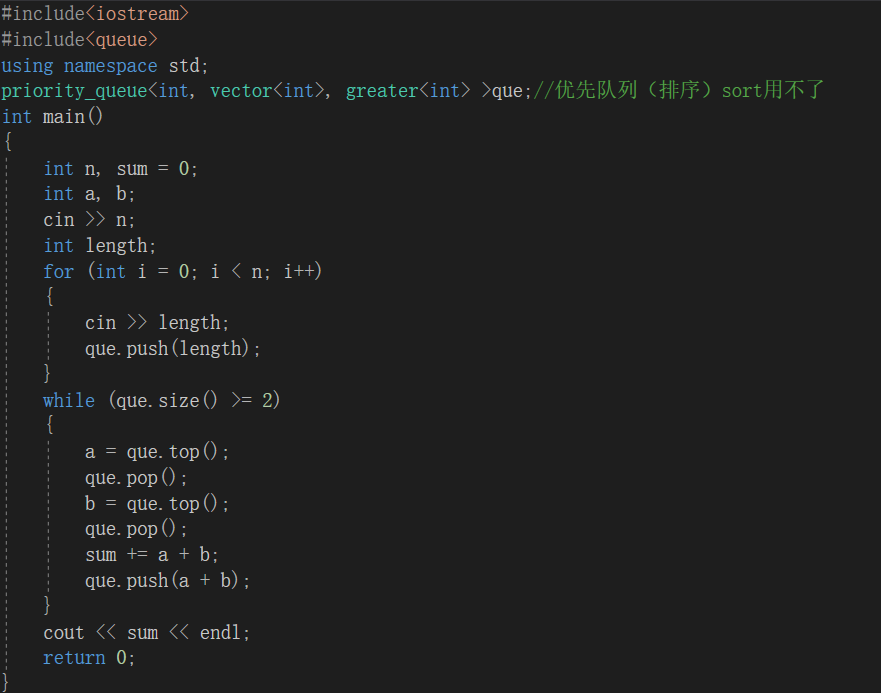
这一题考察了对于哈夫曼树的知识点，唯一的难点在于，排序方法的选取。由于队列不支持用sort函数,所以这里使用优先队列(priority_queue)

//优先队列格式:
priority_queue<结构类型> 队列名; 
//基本操作（与队列queue相同，区别二在于，优先队列会通过堆排序对队列进行排序）:
q.size();//返回q里元素个数
q.empty();//返回q是否为空，空则返回1，否则返回0
q.push(k);//在q的末尾插入k
q.pop();//删掉q的第一个元素
q.top();//返回q的第一个元素
q.back();//返回q的末尾元素

2.3.2代码截图

3、阅读代码

3.1 题目：监控二叉树

给定一个二叉树，我们在树的节点上安装摄像头。节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。计算监控树的所有节点所需的最小摄像头数量。

3.2 解题思路

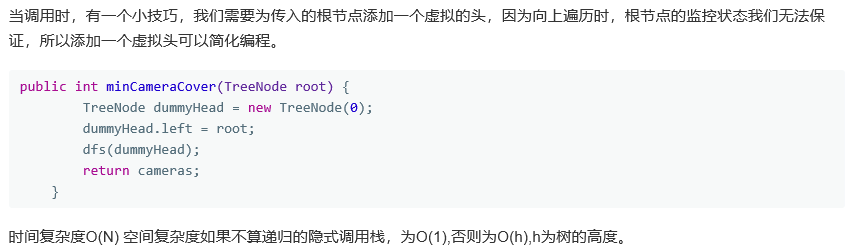
当遍历到一个节点时，我们可以定义三种状态： 0 ： 初始状态，如果节点为null可以返回，也就是不影响其他节点，当两个节点都是0时，我们直接设置当前节点为未监控状态 1： 未监控状态，如果子节点含有该状态，则此节点必须添加摄像头，同时返回当前状态为监控态 2： 监控态，表明此节点已经被监控，当子节点为此状态时，父节点不需要添加摄像头，可以返回初始态

3.3 代码截图

3.4 学习体会