四则运算表达式求解
四则运算表达式求解
这次写了一个能够实现简单四则运算(+,-,*,/,含括号)的小程序。首先分析一下功能需求与限定吧。
需求与限定
- 输入四则运算表达式,要求用户输入其计算的结果,程序能够判断用户输入是否正确。
- 算式输入的数据为正整数或者正分数,用户输入计算结果为整数或分数(分数以“a/b”的形式表示)。
- 统计用户输入正确的答案个数以及错误的答案个数。
分析
首先不难想到,程序的整体设计思路分为两部分,一部分是中缀表达式转换为后缀表达式,另一部分就是后缀表达式的计算。但在实现的过程中还有一个难点需要注意,就是分数在整个程序运行过程中的存储以及计算。由于输入的限定,分数一定是以“a/b”的形式表示的,所以我们可以将这种表示直接看做两个数相除的形式。由此,解决了输入是分数的问题。计算过程中的分数存储以及分数与整数的计算问题,我们可以通过将整数分数进行规格化的存储来解决,即:我们建立一个表示分数的结构体如下,将整数和分数都以该结构体的形式存储,其中numerator表示分子,denominator表示分母。对于分数a/b的存储方式就是numerator = a,denominator = b,整数c的存储方式就是numerator = c, denominator = 1。通过这样统一规范的存储就使得我们在整个计算的过程变得轻松的多了。
1 typedef long long ll; 2 struct num{ 3 ll numerator, denominator; 4 num(){numerator = 0; denominator = 1;} 5 num(int n) {numerator = n; denominator = 1;} 6 num(int n,int d) {numerator = n; denominator = d;} 7 8 void operator = (num x) 9 { 10 numerator = x.numerator; 11 denominator = x.denominator; 12 } 13 };
实现过程
在实现之初,我们先给出需要的变量的定义,如下:
1 #define maxn 1005 2 3 char nifix[maxn], post[maxn]; 4 char ans[maxn]; 5 int cnt_right, cnt_wrong; 6 bool error; 7 num res, rst;
其中,nifix为输入的算式;
post为转化后的后缀表达式;
ans表示用户输入的结果;
cnt_right, cnt_wrong分别表示用户回答正确的个数以及回答错误的个数;
error标志程序运行过程中是否出错,如:输入的表达式不符合规范,出现除零的情况等;
res表示程序计算出的算式答案;
rst表示用户输入的答案转换为规范化的形式的结果。
中缀表达式转后缀表达式
有了上述一系列的定义,我们就可以开始实现我们的程序了。上面提到程序的实现主要分为两个部分组成,首先我们实现第一部分中缀表达式转换为后缀表达式,中缀表达式转后缀表达式的规则如下:
- 遇到操作数时,直接输出到后缀表达式。
- 遇到左括号时,直接入栈。
- 遇到右括号时,出栈,将栈顶元素直接添加到后缀表达式后,直到遇到左括号(左括号出栈但不添加到后缀表达式中)。
- 遇到操作符时,若栈为空,则直接入栈;若栈不空,则比较栈顶操作符和该操作符优先级,若栈顶操作符优先级(*,/优先级大于+,-优先级)大于等于该操作符,则出栈并输出到后缀表达式中。重复操作直至栈空或不符合出栈规则。然后将该操作符入栈。
- 最后将栈中元素依次出栈输出到后缀表达式中。
上述的规则能够实现将一个中缀表达式转化为后缀表达式。但是,我们不能保证用户输入的合法性,及用户可能输入不符合中缀表达式规则的式子如:12*]-3。所以我们的程序必须实现对错误的判断功能,不能因为错误的输入导致程序崩溃或者计算出错误的答案等等。根据我的总结,输入的中缀表达式的错误可以分为几类:
- 输入字符串中包含非表达式的字符如:a, b, c, [, &, .等等。
- 输入的字符串中括号不匹配,包括缺少左括号如:1+2)*3,缺少右括号如:1*(2+3等。
- 连续两个符号在一块包括++,+-等但不包括‘(’左边为‘+’‘-’‘*’‘/’和‘)’右边为‘+’‘-’‘*’‘/’。
有了以上的分析我们就可以开始具体实现了。首先我们要实现几个功能性函数,如下:
1 bool isNum(char x) //判断是否是数字 2 { 3 return (x >= '0' && x <= '9'); 4 } 5 6 bool isOp(char x) //判断是否是操作符 7 { 8 return (x == '+' || x == '-' || x == '*' || x == '/' || x == '(' || x == ')'); 9 } 10 11 int priority(char x) //返回一个操作符的优先级 12 { 13 if (x == '-' || x == '+') 14 return 1; 15 else if (x == '*' || x == '/') 16 return 2; 17 else if (x == '(') 18 return 0; 19 else 20 return -1; 21 }
然后就是中缀转后缀的主函数了,实现如下:
1 bool nifix_to_post() 2 { 3 memset(post, 0, sizeof(post)); 4 stack<char> s; //操作符栈,用来压操作符 5 /* ************************************************************************************************ 6 # 由于操作数是多位的,所以我们逐位做一个累加暂存的工作,当遇到操作符时,代表此操作符前的数暂存完毕, 7 # 需要将其入栈,但也不是所有操作符前都有操作数,如'*('等,所以我们需要一个标志位来表示某个操作符前 8 # 是否进行过暂存操作数的处理。 9 *///************************************************************************************************** 10 bool havenum = false; 11 int tmp = 0, pos = 0; //tmp为暂存多位数的变量,pos为后缀数组存储位置 12 for (int i = 0; nifix[i] != '\0'; i++) //循环遍历中缀数组 13 { 14 if (isNum(nifix[i])) //若当前字符是数字,则进行暂存操作。并标识已有操作数 15 { 16 havenum = true; 17 tmp = tmp*10 + (nifix[i]-'0'); 18 } 19 else if (isOp(nifix[i])) //若当前字符是操作符则进行如下操作 20 { 21 //中缀表达式合法性判断,判断是否有连续两个字符相连,若有则代表出错 22 if (isOp(nifix[i-1]) && nifix[i-1] != ')' && nifix[i] != '(') 23 return true; 24 //如果操作符前有操作数,则将得到的操作数输出至后缀表达式 25 if (havenum) 26 { 27 havenum = false; 28 post[pos++] = tmp + '0'; 29 tmp = 0; 30 } 31 //如果操作符为右括号,则按规则进行出栈如后缀表达式等操作 32 if (nifix[i] == ')') 33 { 34 if (s.empty()) //中缀表达式合法性判断,判断括号匹配 35 return true; 36 while(s.top() != '(') 37 { 38 post[pos++] = s.top(); 39 s.pop(); 40 if (s.empty()) //中缀表达式合法性判断,判断括号匹配 41 return true; 42 } 43 s.pop(); 44 } 45 else if (nifix[i] == '(') //如果是左括号则直接入栈 46 s.push(nifix[i]); 47 else //如果是+-*/则按规则操作 48 { 49 while (!s.empty() && priority(nifix[i]) <= priority(s.top())) 50 { 51 post[pos++] = s.top(); 52 s.pop(); 53 } 54 s.push(nifix[i]); 55 } 56 } 57 else //中缀表达式合法性判断,判断是否含非法符号 58 return true; 59 } 60 //若有操作数,则将其输出至后缀表达式 61 if (havenum) 62 { 63 havenum = false; 64 post[pos++] = tmp + '0'; 65 tmp = 0; 66 } 67 //将栈中操作符一次输出到后缀表达式中 68 while(!s.empty()) 69 { 70 if (s.top() == '(') //中缀表达式合法性判断,判断括号匹配 71 return true; 72 post[pos++] = s.top(); 73 s.pop(); 74 } 75 return false; 76 }
至此,中缀表达式转后缀表达式的算法就完成了,同时在这个过程中还完成了对输入中缀表达式合法性的判断。
后缀表达式计算
在这一部分,我们要完成的事情就比较简单了。唯一要注意的就是对操作数进行分数形式的计算,由于整数和分数都被我们表示为分数的形式,所以对两个数a/b和c/d,这两个数的四则运算操作规则如下:
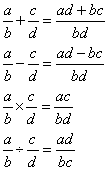
有了运算规则,我再简要的阐述一下后缀表达式求值的方法:
- 从左到右扫描后缀表达式,遇到运算符就把表达式中该运算符前面两个操作数取出并运算,然后把结果带回后缀表达式;继续扫描直到后缀表达式最后一个表达式。
在后缀表达式计算过程中,我们同样需要判断后缀表达式计算的合法性,经过分析,我得到如下几种引起错误的可能:
- 当遇到一个操作符时,栈内没有足够的操作数供以运算。
- 当操作符都读取完毕后,栈内有超过一个的操作数。
- 除数为0。
之后,我们就可以开始编写后缀表达式求值部分的算法,由上述分数运算规则,并且由于我们所设计的结构体分子分母是分开的,所以还需要解决分子分母约分的问题,所以我们首先需要编写求分子分母最大公约数的函数,我们用辗转相除法实现如下(具体算法描述不在此阐述):
1 ll gcd(ll m, ll n) 2 { 3 ll tmp; 4 tmp = m % n; 5 while(tmp) 6 { 7 m = n; 8 n = tmp; 9 tmp = m % n; 10 } 11 return n; 12 }
有了上述函数,就可以开始实现后缀表达式计算的过程了,其函数实现如下:
1 bool cal_result() 2 { 3 stack<num> s; //用来存放操作数的栈 4 for (int i = 0; i < strlen(post); i++) //循环遍历后缀表达式 5 { 6 if (!isOp(post[i])) //如果是数字则直接入栈 7 { 8 num tmp(post[i]-'0', 1); 9 s.push(tmp); 10 } 11 else 12 { 13 //取出两个操作数,如果操作数数量不够,则出错,返回 14 if (s.empty()) 15 return true; 16 num b = s.top(); s.pop(); 17 if (s.empty()) 18 return true; 19 num a = s.top(); s.pop(); 20 num c; 21 22 if (post[i] == '+') //操作符是'+',进行上述规则运算 23 { 24 c.numerator = a.numerator * b.denominator + b.numerator * a.denominator; 25 c.denominator = a.denominator * b.denominator; 26 } 27 else if (post[i] == '-') //操作符是'-',进行上述规则运算 28 { 29 c.numerator = a.numerator * b.denominator - b.numerator * a.denominator; 30 c.denominator = a.denominator * b.denominator; 31 } 32 else if (post[i] == '*') //操作符是'*',进行上述规则运算 33 { 34 c.numerator = a.numerator * b.numerator; 35 c.denominator = a.denominator * b.denominator; 36 } 37 else if (post[i] == '/') //操作符是'/',进行上述规则运算 38 { 39 if (b.numerator == 0) //如果除的是0,则出现除法错误,返回 40 return true; 41 c.numerator = a.numerator * b.denominator; 42 c.denominator = a.denominator * b.numerator; 43 } 44 else //其他情况则出错 45 return true; 46 if (c.numerator != 0) //若结果不为0,则对分子分母约分 47 { 48 ll div = gcd(c.denominator, c.numerator); 49 c.denominator /= div; 50 c.numerator /= div; 51 } 52 s.push(c); //将约分后结果入栈 53 } 54 } 55 if (s.size() > 1) //如果所有操作符都进行相应操作数后栈内还有多个元素,则说明出错,返回 56 return true; 57 res = s.top(); //保存结果 58 s.pop(); 59 if (res.denominator < 0) //化简结果,将分母的负号移到分子上 60 { 61 res.numerator = -res.numerator; 62 res.denominator = -res.denominator; 63 } 64 return false; 65 }
经过上述的操作,我们将一个输入的中缀表达式成功计算出结果,接下来要做的就是编写接收用户输入并进行判断了。
用户输入结果转化
用户输入的答案理论上讲是一个只包含数字和'/'的字符串,对于用户的输入,我们只能通过字符串接收,然后将其转化成我们需要的形式,实现方式也很简单,当然我们也要对用户输入答案的合法性进行判断,代码如下:
1 bool trans_ans() 2 { 3 int i = 0; 4 ll tmp = 0; 5 //两个标志位分别标志用户输入的分子分母是否为负数 6 bool num_flag = false, deno_flag = false; 7 //先判断分子是否为负 8 if (ans[i] == '-') 9 { 10 num_flag = true; 11 i++; 12 } 13 //接收第一个数字 14 while(isNum(ans[i])) 15 { 16 tmp = tmp * 10 + (ans[i] - '0'); 17 i++; 18 } 19 //若第一个数为负数,则将转化过来的整数取负 20 if (num_flag) 21 tmp = -tmp; 22 //保存分子 23 rst.numerator = tmp; 24 //分母赋初值为1 25 rst.denominator = 1; 26 tmp = 0; 27 //判断是否是分数 28 if (ans[i] == '/') 29 { 30 //判断分母是否为负数 31 if (ans[++i] == '-') 32 { 33 deno_flag = true; 34 i++; 35 } 36 //接收第二个数 37 while(isNum(ans[i])) 38 { 39 tmp = tmp * 10 + (ans[i] - '0'); 40 i++; 41 } 42 //若第二个数为负数,则将转化过来的整数取负 43 if (deno_flag) 44 tmp = -tmp; 45 //保存分母 46 rst.denominator = tmp; 47 } 48 //若分母为0,则用户输入的结果是非法的 49 if (rst.denominator == 0) 50 return true; 51 //若此时没有遍历所有的字符,则说明输入是非法的 52 if (i != strlen(ans)) 53 return true; 54 //化简分母的负号,将其移至分子 55 if (rst.denominator < 0) 56 { 57 rst.numerator = -rst.numerator; 58 rst.denominator = -rst.denominator; 59 } 60 //若用户输入的分子分母都是负数,则用户输入不符合规范,我们取分母为0(因为计算结果不可能出现分母为0的状况)标志这种情况的发生 61 if (num_flag && deno_flag) 62 rst.denominator = 0; 63 return false; 64 }
主函数的实现
最后就剩下主函数了,其具体实现如下:
1 int main() 2 { 3 //计数器请0 4 cnt_right = cnt_wrong = 0; 5 cout << "Now test begins..." << endl; 6 while(cin >> nifix) 7 { 8 error = nifix_to_post(); //中缀转后缀,并接受错误信息 9 if (error) //若过程出错,则输出错误信息 10 { 11 cout << "There is an illegal equation!" << endl; 12 return 0; 13 } 14 15 //test_post(); 16 17 error = cal_result(); //后缀表达式计算,并接受错误信息 18 if (error) //若过程出错,则输出错误信息 19 { 20 cout << "There is something wrong during computing..." << endl; 21 return 0; 22 } 23 24 cout << "Please enter your answer: "; 25 cin >> ans; //接受用户答案 26 error = trans_ans(); //答案翻译, 并接受错误信息 27 if (error) //若过程出错,则输出错误信息 28 { 29 cout << "You have inputted an illegal answer!" << endl; 30 return 0; 31 } 32 //若用户输入和城西计算答案的分子分母相等或分子均为0,则说明用户输入答案正确 33 if ((rst.denominator == res.denominator && rst.numerator == res.numerator) || (rst.numerator == res.numerator && rst.numerator == 0)) 34 { 35 cnt_right++; 36 cout << "Right answer!" << endl; 37 } 38 //否则答案错误,程序输出正确答案 39 else 40 { 41 cnt_wrong++; 42 cout << "You have entered a wrong answer. The right answer is "; 43 if (res.denominator == 1) 44 cout << res.numerator << "." << endl; 45 else 46 cout << res.numerator << "/" << res.denominator << "." << endl; 47 } 48 } 49 cout << "test ends..." << endl; 50 //输出统计结果 51 cout << "You have answered " << cnt_right+cnt_wrong << " problems in total "; 52 cout << "in which " << cnt_right << " are correct and " << cnt_wrong << " are wrong." << endl; 53 return 0; 54 }
总结
这次写的这个程序有一定优点,也存在一些缺点。我认为优点就是整个程序的鲁棒性很好,不会意外崩溃,对于所有可能出现的错误有较全面的考虑,并都对其进行了处理。缺点也有一些,比如程序在输入时不支持负数的运算。所以整个程序还是有提升的空间的。在整个写码的过程中,也学到了很多,也加强了我对算法实现的能力,总体的收获还是很大的。

