栈

栈（stack）又称堆栈

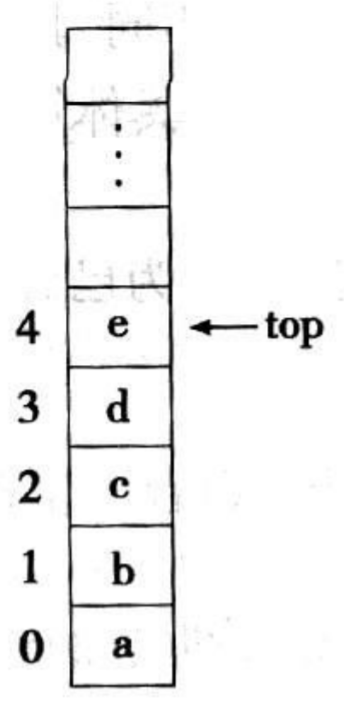
是限定只在表尾进行插 入或删除操作的线性表。 栈S = ( a1 , a2 , …，an ) 是按a1 , a2 , …，an次序进栈的，a1为栈底元素，an 为栈顶元素。

栈的修改是按先进后出原则进行的，所以栈又称 后进先出（Last In First Out）的线性表。简称LIFO结 构。先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据（最后一个数据被第一个读出来）。对栈的插入与删除操作中，不需要改变栈底指针。

栈的存储：

顺序：

• top = -1 ： 栈空
• top =StackMaxSize-1 ： 栈满
• 压栈 ： top++，然后再赋值
• 出栈 ： 先取出栈顶元素，再 top - -
• 即：插入删除是在顺序表的表尾进行的
• 时间复杂度 ：O(1)

 链式存储：

栈的应用：

1）：反序输出 

2）：括号匹配 （左括弧入栈，右括弧出栈）

         假设在表达式中 （［］（））或［（［ ］［ ］）］ 等为正确的格式， ［（ ］）或（［（ ））或 (( )]) 均为不正确的格式。

        凡出现左括弧，则进栈； 凡出现右括弧，首先检查栈是否空 若栈空，则表明该“右括弧”多余 否则和栈顶元素比较， 若相匹配，则“左括弧出栈” 否则表明不匹配          表达式检验结束时， 若栈空，则表明表达式中匹配正确 否则表明“左括弧”有余

3）数制转换：余数入栈，最后出栈

 

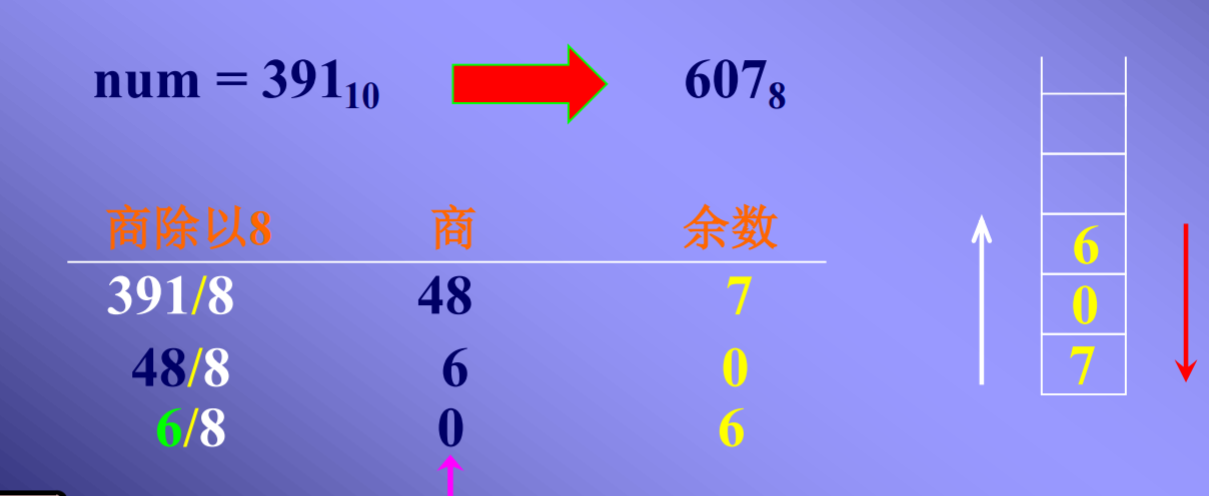
4）：算术表达式的计算：

算术表达式的两种表示S1 第一个操作数，OP 运算符 S2 第二个操作数

中缀表达式：S1 + OP + S2 为中缀表示法

后缀表达式（逆波兰式）：S1 + S2 + OP 为后缀表示法

如何从后缀式求值？a b × c d e / - f ×  + 最终结果为：a×b+(c-d/e)×f

从左向右扫描，遇到数字时，将数字压入栈，遇到运算符时候，把栈内前两个数字弹出，先弹出的数字放在运算符后面，然后进行相应运算，并将计算结果入栈。重复直到表达式最右端。

例：后缀表达式是34+5*6- （从左向右扫描）

a) 将数字3,4依次入栈；

b) 遇见运算符+，依次弹出4，3，计算3+4=7，将7入栈继续扫描；

c) 将5入栈；

d) 遇见运算符*，依次弹出5，7，计算7*5=35，将35入栈继续扫描；

e) 将6入栈；

f) 遇见运算符-，依次弹出两个6，35，计算35-6=29，将29入栈继续扫描

扩展：

例1：若已知一个栈的进栈序列是1,2,3,…,n，元素出栈后马上进入队列， 已知队列输出序列为p1,p2,p3,…,pn,若 1=3,试讨论p2的可能性

答案：一定不是1，可能为2，也可能为其他值

例2：设栈S和队列Q的初始状态为空，元素a1,a2,a3,a4,a5,a6,a7,a8依次通过栈S， 一个元素出栈后立即进入队列Q，若8个 元素出队列的次序是 a3,a6,a7,a5,a8,a4,a2,a1，则栈S的容量至

少应该是多少？（即至少应该容纳多少个元素？）

答案：5