数据结构（一）树

树

是由n≥0 个结点组成的有穷集合以及结点之间关系组成的集合构成的结构,是一种一对多的数据结构。

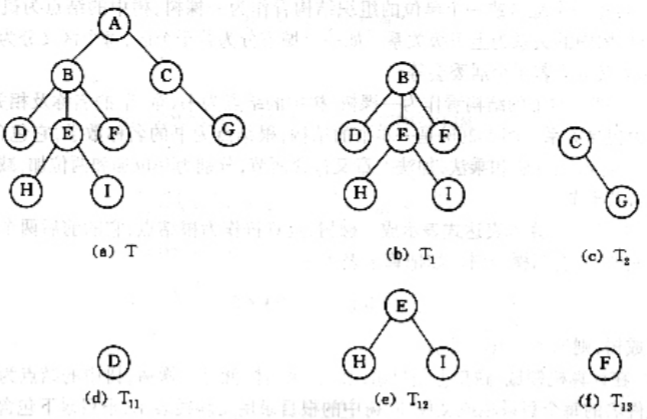
  特点：

1. 有且仅有一个结点没有前驱结点,该结点为树的根结点。

2. 除了根结点外,每个结点有且仅有一个直接前驱结点。

3. 包括根结点在内，每个结点可以有多个后继结点。

树的术语：

1. 结点的度：该结点拥有的子树的数目。

2. 树的度：树中结点度的最大值。

3. 叶结点：度为0 的结点。

4. 分支结点:度非0 的结点。

5. 层次的定义:根结点为第一层,若某结点在第i 层, 则其孩子结点(若存在)为第i+1层。

6.树的深度: 树中结点所处的最大层次数。如下为h=3

7.树的有序性: 若树中结点的子树的相对位置不能 随意改变, 则称该树为有序树，否 则称该树为无序树。

  

树的性质

性质1: 树中结点个数等于所有结点的度数加1。　　

      A的结点=3，B结点=3，C结点=1，X结点=2   结点个数=（3+3+1+2）+1=10

性质2:  度为k的树中第i层上至多有k （i -1）次方 个结点（i≥1） 。

　　k=3 第3层的结点数=3(3-1)=3的2次方=6 所以树为3第三层有6个结点

性质3 深度为h的k叉树中至多有(k*h-1)/(k-1) 结点。 满k叉树：结点个数等于(kh-1)/(k-1) 的k叉树。 (kh-1)为k的h次方在减1　　

性质4 具有n个结点的k叉树的最小深度为logk(n(k-1)+1)

  二叉树：度为2的有序树

 

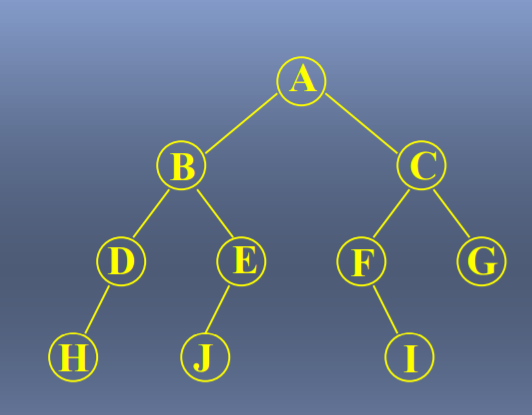
1. 一棵非空二叉树的第i 层最多有2的(i–1)次方个结点(i≥1)。比如第二层有多少个结点 n=2的(2-1)次方=2

2.深度为h的非空二叉树最多有2的h次方-1个结点.

3.若非空二叉树有n0个叶结点,有n2个度为2的结点, 则 n0=n2+1

4.具有n个结点的完全二叉树的深度h=[log2n]+1.

二叉树的遍历：前序遍历（DLR），中序遍历（LDR），后序遍历（LRD），层次遍历 

 

   

 

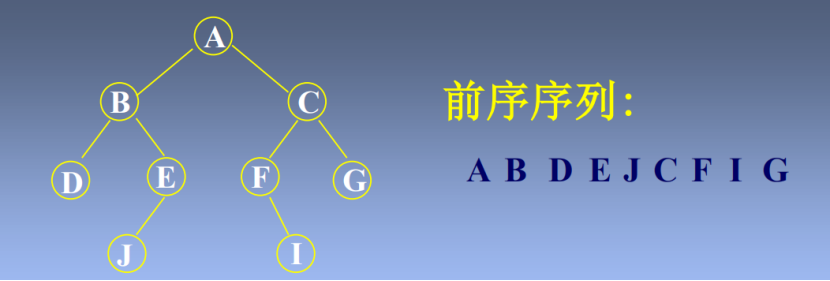
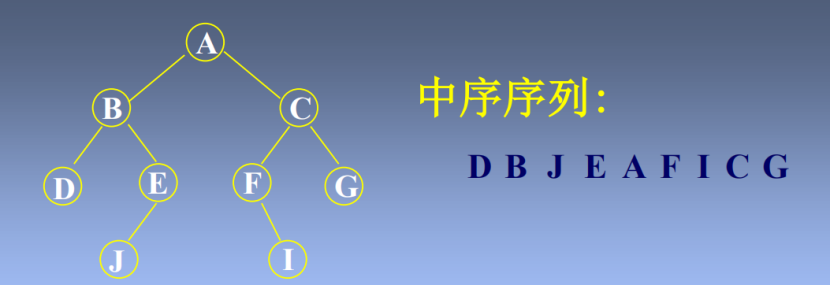
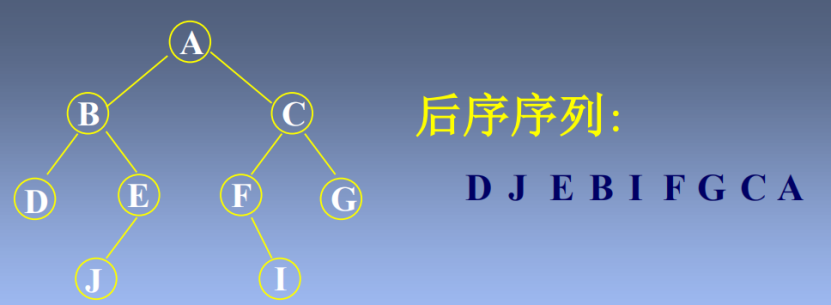
如何由遍历次序恢复二叉树？ 

已知一棵二叉树的后序遍历次序为DEBGFCA，中序遍历次序为DBEACGF，求该二叉树的前序遍历次序 答案：ABDECFG 

提示：从后序遍历次序中找根结点，再从中序遍历次序中找相应根节结点的左子树和右子树

 

 二叉树的存储：

顺序存储： 15=2的h次方-1=2的4次方-1=15

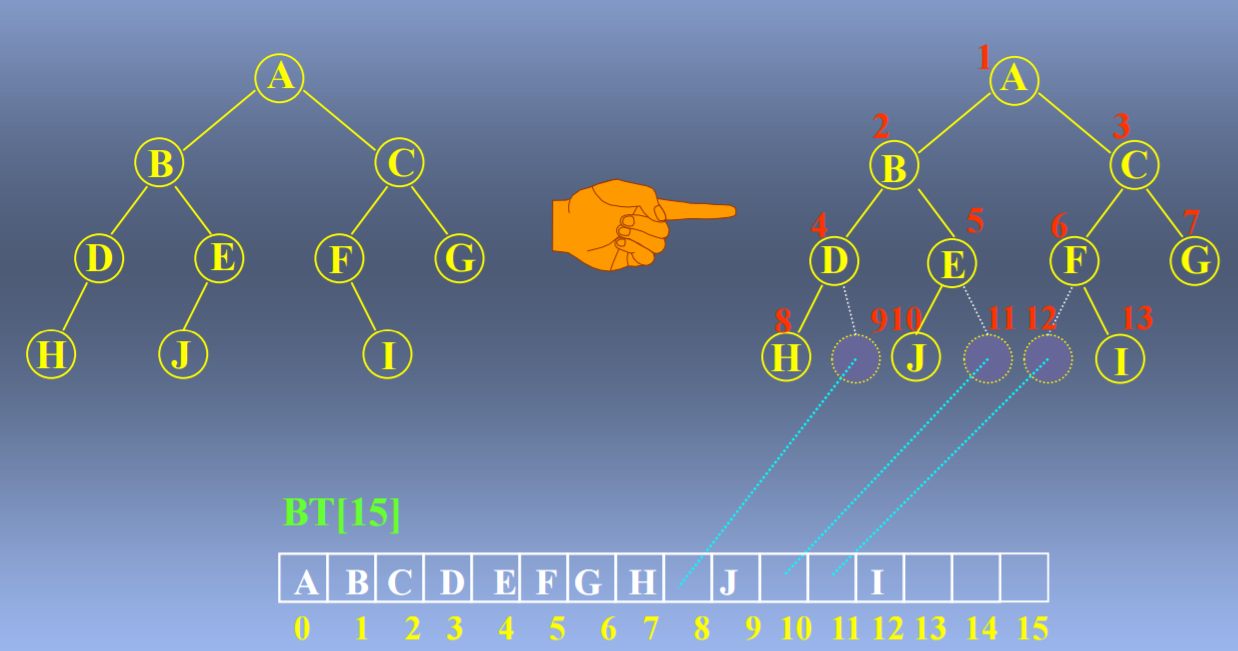
 链式存储：

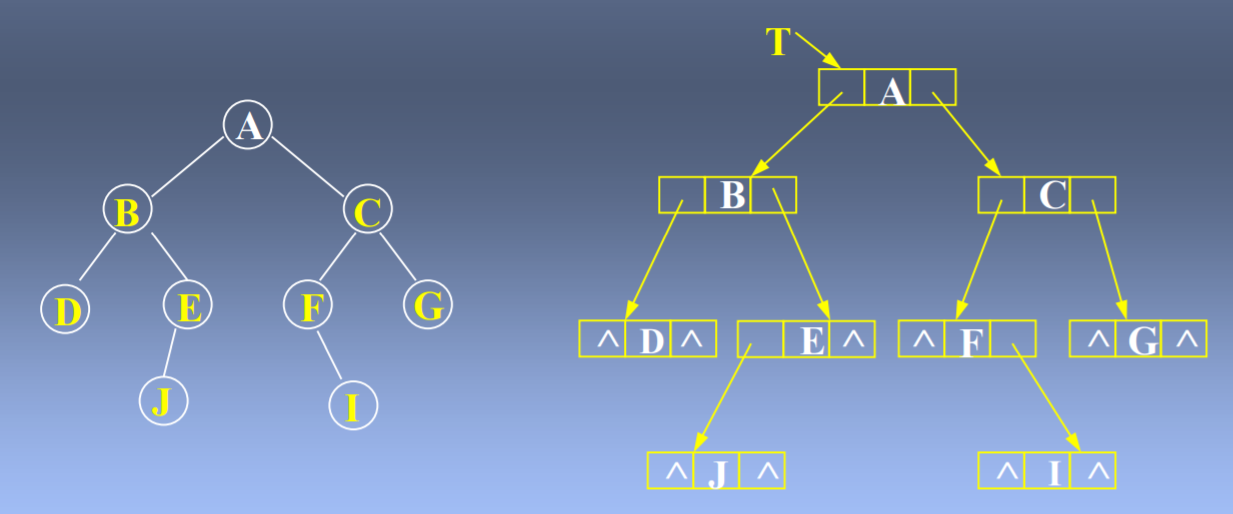
 满二叉树

若一棵二叉树中的结点, 或者为叶结点， 或者具有两棵非空子树,并且叶结点都集中在二叉树的最下面一层.这样的二叉树为满二叉树.

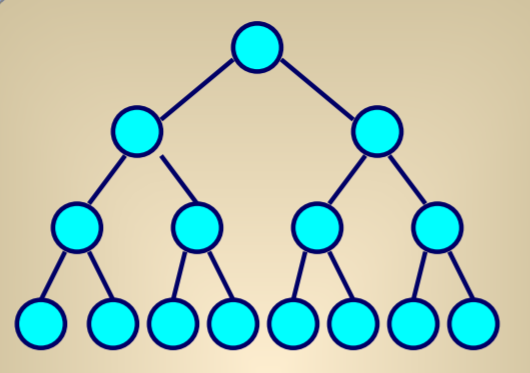
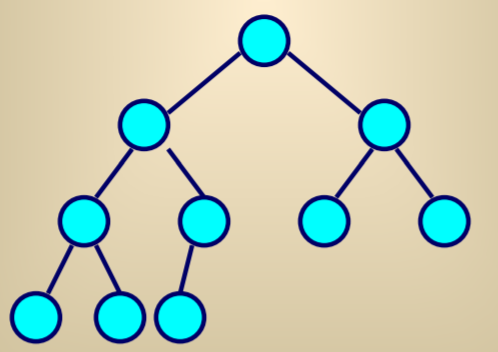
 完全二叉树

若一棵二叉树中只有最下面两层的结点的度可以小于2, 并且最下面一层的结点(叶结点)都依次排列在该层从左至右的位置上。这样的二叉树为完全二叉树.

  性质：

1、深度为h的完全二叉树的前h-1层为满二叉树

2、完全二叉树最多只有一个度为1的分支节点

求深度为h的完全二叉树的总结点数的范围。答案：2(h-1）次方, 2（h）-1

二叉排序/搜索树

二叉排序/搜索树的定义 ：二叉排序树Binary Sort Tree：或者为一棵空树，或者为具有下列特性的非空树：

1、若其左子树非空，则左子树上的所有结点的关键字值均小于根结点关键字值；

2、若其右子树非空，则右子树上的所有结点的关键字值均大于等于根结点关键字值；

3、其左、右子树分别为二叉排序树。 

例：已知一组元素为(46,25,78,62,12,37,70)，画出按元素排列顺序输入生成的一棵二叉搜索树， 

哈夫曼树 

1、定义：哈夫曼树（Huffman）树，又称最优树，是一种带权路径长度WPL（树带权路径长度之和叶子节点相加*层数从0开始）最小的二叉树 

例2：设给定权集w={2,3,4,7,8,9},试构造关于w的一棵哈夫曼树，并求其加权 路径长度WPL. 

  WPL=叶子节点相加*层数从0开始