算法复杂度

 1常数阶

例：代码的大O是多少？ 

int sum = 0, n = 100;
printf(“abc\n”);
sum = (1+n)*n/2;

 第一条就说明了所有加法常数给他个O(1)即可

 

2线性阶：一般含有非嵌套循环涉及线性阶，线性阶就是随着问题规模n的扩大，对应计算次数呈直线增长。

int i , n = 100, sum = 0;
for( i=0; i < n; i++ )
{
    sum = sum + i;//随着n的增大，执行的次数越多 时间复杂度为O（n）
}

 

3平方阶  

int i, j, n = 100;
for( i=0; i < n; i++ )
{
    for( j=0; j < n; j++ )
    {
        printf(“ssm”);
    }
}

 n等于100，也就是说外层循环每执行一次，内层循环就执行100次，那总共程序想要从这两个循环出来，需要执行100*100次，也就是n的平方。所以这段代码的时间复杂度为O(n^2)。

总结：如果有三个这样的嵌套循环就是n^3。所以总结得出，循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数。

int i, j, n = 100;
for( i=0; i < n; i++ )
{
    for( j=i; j < n; j++ )
    {
        printf(“ssm\n”);
    }
}

由于当i=0时，内循环执行了n次，当i=1时，内循环则执行n-1次……当i=n-1时，内循环执行1次，所以总的执行次数应该是：

n+(n-1)+(n-2)+…+1 = n(n+1)/2
n(n+1)/2 = n^2/2+n/2
用我们推导大O的攻略，第一条忽略，因为没有常数相加。第二条只保留最高项，所以n/2这项去掉。第三条，去除与最高项相乘的常数，最终得O(n^2)。

 

4对数阶 

int i = 1, n = 100;

while( i < n )
{
    i = i * 2;
}

由于每次i*2之后，就距离n更近一步，假设有x个2相乘后大于或等于n，则会退出循环。

于是由2^x = n得到x = log(2)n，所以这个循环的时间复杂度为O(logn)。

 

 

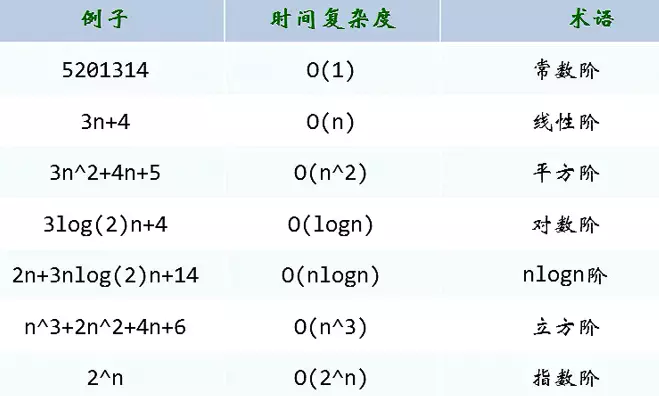
对应的线性图：

 

 

 

 

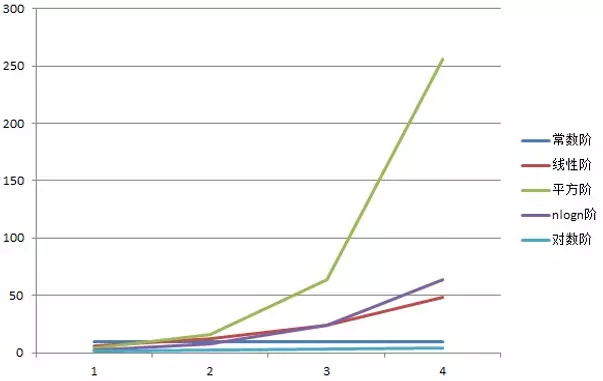
常用的时间复杂度所耗费的时间从小到大依次是：
O(1) < O(logn) <O (n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)