Java 数据结构总结
1. 链表
链表(LinkedList) 虽然是一种线性表,但是并不会按线性的顺序存储数据,使用的不是连续的内存空间来存储数据
链表的插入和删除操作的复杂度为 O(1) ,只需要知道目标位置元素的上一个元素即可。但是,在查找一个节点或者访问特定位置的节点的时候复杂度为 O(n)
使用链表结构可以克服数组需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但链表不会节省空间,相比于数组会占用更多的空间,因为链表中每个节点存放的还有指向其他节点的指针。除此之外,链表不具有数组随机读取的优点
1.1 单向链表
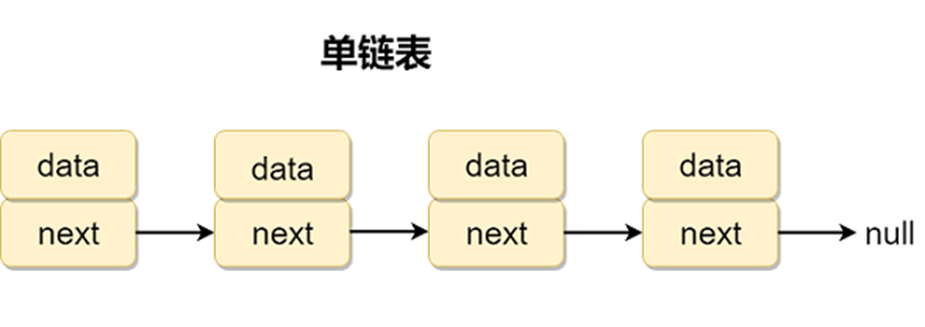
单向链表只有一个方向,结点只有一个后继指针 next 指向后面的节点。因此,链表这种数据结构通常在物理内存上是不连续的。我们习惯性地把第一个结点叫作头结点,链表通常有一个不保存任何值的 head 节点(头结点),通过头结点我们可以遍历整个链表。尾结点通常指向 null
1.1.1 定义节点类 Node
节点类:
@NoArgsConstructor
@AllArgsConstructor
public class Node<T> {
T val; // 节点值
public Node next; // 指向后续节点
Node(T val) {
this.val = val;
}
}
1.1.2 直接对节点类操作
1. 生成链表
public static void main(String[] args) {
Node head = new Node();
Node node1 = new Node<>("王五");
Node node2 = new Node<>(1);
Node node3 = new Node<>("李四");
Node node4 = new Node<>(2);
head.next = node1;
node1.next = node2;
node2.next = node3;
node3.next = node4;
}
2. 遍历链表
queryAll(head);
public static void queryAll(Node node){
Node currentNode = node;
while (currentNode.next != null){
currentNode = currentNode.next;
System.out.println(currentNode.val);
}
}
3. 直接添加
Node addNode = new Node("赵六");
head = add(head, addNode);
public static Node add(Node head, Node addNode){
Node currentNode = head;
// 找到链表的最后一个节点
while (currentNode.next != null){
currentNode = currentNode.next;
}
// 让该节点的后一个节点为添加的节点,即将该节点添加到链表
currentNode.next = addNode;
return head;
}
4. 添加到指定位置
Node addIndexNode = new Node("11");
head = add(head, addIndexNode, 2);
public static Node add(Node head, Node addNode, int index) throws Exception {
Node currentNode = head;
// 找到指定位置的上一个节点
for (int i = 0; i < index - 1; i++) {
currentNode = currentNode.next != null ? currentNode.next : null;
if (currentNode == null) {
throw new Exception("位置不存在");
}
}
// 让添加节点的下一个节点为该节点的下一个节点
addNode.next = currentNode.next;
// 再让该节点的下一个节点为添加节点,即在指定位置插入一个节点
currentNode.next = addNode;
return head;
}
5. 删除指定位置的元素
head = delete(head, 4);
public static Node delete(Node head, int index) throws Exception {
Node currentNode = head;
// 找到指定位置的上一个节点
for (int i = 0; i < index - 1; i++) {
currentNode = currentNode.next != null ? currentNode.next : null;
if (currentNode == null) {
throw new Exception("位置不存在");
}
}
// 该节点的下一个节点就是要删除的节点
Node delNode = currentNode.next;
// 让该节点的下一个节点为删除节点的下一个节点,指定位置的节点就被删除了
currentNode.next = delNode.next;
return head;
}
完整示例如下:
public static void main(String[] args) throws Exception {
Node head = new Node();
Node node1 = new Node<>("王五");
Node node2 = new Node<>(1);
Node node3 = new Node<>("李四");
Node node4 = new Node<>(2);
head.next = node1;
node1.next = node2;
node2.next = node3;
node3.next = node4;
Node addNode = new Node("赵六");
head = add(head, addNode);
Node addIndexNode = new Node("11");
head = add(head, addIndexNode, 2);
head = delete(head, 4);
queryAll(head);
}
public static Node delete(Node head, int index) throws Exception {
Node currentNode = head;
for (int i = 0; i < index - 1; i++) {
currentNode = currentNode.next != null ? currentNode.next : null;
if (currentNode == null) {
throw new Exception("位置不存在");
}
}
Node delNode = currentNode.next;
currentNode.next = delNode.next;
return head;
}
public static Node add(Node head, Node addNode, int index) throws Exception {
Node currentNode = head;
for (int i = 0; i < index - 1; i++) {
currentNode = currentNode.next != null ? currentNode.next : null;
if (currentNode == null) {
throw new Exception("位置不存在");
}
}
addNode.next = currentNode.next;
currentNode.next = addNode;
return head;
}
public static Node add(Node head, Node addNode) {
Node currentNode = head;
while (currentNode.next != null) {
currentNode = currentNode.next;
}
currentNode.next = addNode;
return head;
}
public static void queryAll(Node node) {
Node currentNode = node;
while (currentNode.next != null) {
currentNode = currentNode.next;
System.out.println(currentNode.val);
}
}
1.1.3 封装节点操作类
定义一个类,封装对节点进行操作的方法。实现 Iterable 接口,用来遍历
public class LinkNode<T> implements Iterable<T>{
private Node headNode; // 头结点,链表的 headNode 是不可以动的
private int length; // 结点个数
public LinkNode(){
headNode = new Node();
length = 0;
}
// 清空
public void clear(){
headNode.next = null; // 头节点 next 为 null 就是空链表
headNode.val = null;
length = 0;
}
// 是否非空
public boolean isEmpty(){
return length == 0;
}
// 获取长度
public int length(){
return length;
}
// 读取链表第 i 位置的元素值并返回
public T get(int index){
if (index < 0 || index > length){
System.out.println("不存在该位置");
}
// 头指针不可以移动,不然就无法再找到链表
// 定义一个临时的Node也指向头指针,通过该指针来进行操作
Node<T> currentNode = headNode;
for (int i = 0; i < index; i++) {
currentNode = currentNode.next;
}
return currentNode.val;
}
// 插入到链表末尾
public void insert(T val){
Node<T> addNode = new Node<>(val);
Node currentNode = headNode;
// 找到最后一个节点
while (currentNode.next != null){
currentNode = currentNode.next;
}
currentNode.next = addNode;
length++;
}
// 插入到 i 位置
public void insert(T val, int index){
if (index < 0 || index > length){
System.out.println("不存在该位置");
}
Node currentNode = headNode;
for (int i = 0; i < index - 1; i++) {
currentNode = currentNode.next;
}
Node<T> addNode = new Node<>(val);
addNode.next = currentNode.next;
currentNode.next = addNode;
length++;
}
// 移除并返回 i 位置的元素值
public T remove(int index){
if (index < 0 || index > length){
System.out.println("不存在该位置");
}
Node currentNode = headNode;
for (int i = 0; i < index - 1; i++) {
currentNode = currentNode.next;
}
// 要删除的节点
Node<T> delCurrent = currentNode.next;
currentNode.next = delCurrent.next;
length --;
return delCurrent.val;
}
// 查找元素在链表中第一次出现的位置,索引值
public int indexOf(T value){
Node currentNode = headNode;
for (int i = 0; currentNode.next != null; i++) {
currentNode = currentNode.next;
if (currentNode.val.equals(value)){
return i;
}
}
return -1;
}
@Override
public Iterator<T> iterator() {
return new Iterator<T>() {
Node currentNode = headNode;
@Override
public boolean hasNext() {
return currentNode.next != null;
}
@Override
public T next() {
currentNode = currentNode.next;
return (T) currentNode.val;
}
};
}
}
测试类:
public static void main(String[] args) {
LinkNode linkNode = new LinkNode<>();
// LinkNode<String> linkNode = new LinkNode<>(); // 限制泛型
linkNode.insert("张三11");
linkNode.insert(22);
linkNode.insert("王五33");
for (Object o : linkNode) {
System.out.print(o + " ");
}
System.out.println();
linkNode.insert("赵六", 2);
for (Object o : linkNode) {
System.out.print(o + " ");
}
System.out.println();
System.out.println("删除的元素:" + linkNode.remove(3));
for (Object o : linkNode) {
System.out.print(o + " ");
}
System.out.println();
System.out.println(linkNode.indexOf("赵六"));
}
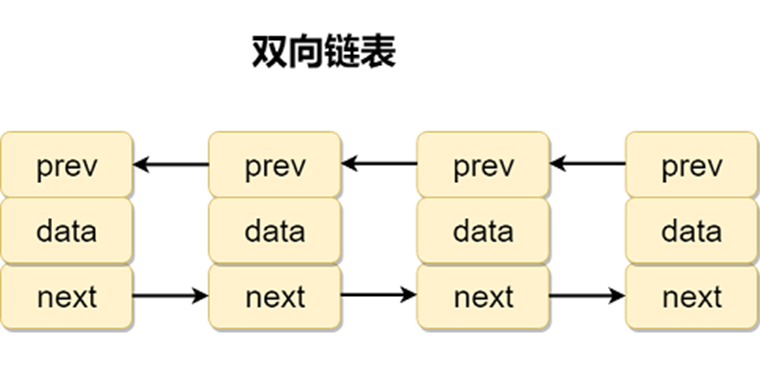
1.2 双向链表
包含两个指针,一个 prev 指向前一个节点,一个 next 指向后一个节点
1.2.1 定义节点类
@AllArgsConstructor
@NoArgsConstructor
public class DoubleNode<T> {
T val;
DoubleNode prev;
DoubleNode next;
public DoubleNode(T val) {
this.val = val;
}
}
1.2.2 封装节点操作类
public class DoubleLinkNode<T> {
private DoubleNode head;
private DoubleNode last;
private int length;
public DoubleLinkNode(){
length = 0;
}
// 遍历
public void queryAll(){
DoubleNode currentNode = head;
while (currentNode != null){
System.out.print(currentNode.val + " ");
currentNode = currentNode.next;
}
System.out.println();
}
// 获取长度
public int getLength(){
return length;
}
// 头插法
public void addFirst(T val){
// 插入的节点
DoubleNode addNode = new DoubleNode(val);
// 加入链表为空,则插入的节点就是头节点和尾结点
if (head == null){
head = addNode;
last = addNode;
length ++;
} else {
// 让添加节点的下一个节点为头结点
addNode.next = head;
// 再让头结点的上一个为添加节点
head.prev = addNode;
// 再把头节点设为添加节点
head = addNode;
length ++;
}
}
// 尾插法
public void addLast(T val){
DoubleNode addNode = new DoubleNode(val);
if (head == null){
head = addNode;
last = addNode;
length ++;
} else {
// 让尾结点的下一个节点为添加节点
last.next = addNode;
// 再让添加节点的上一个为尾结点
addNode.prev = last;
// 再把尾结点设为添加节点
last = addNode;
length ++;
}
}
// 在任意位置插入
public void addIndex(T val, int index) throws Exception {
// 假如添加位置为头结点位置,就是头插法
if (index <= 0){
addFirst(val);
return;
}
// 假如添加位置为尾结点的位置,就是尾插法
if (index > length){
addLast(val);
return;
}
DoubleNode addNode = new DoubleNode(val);
DoubleNode currentNode = head;
// 找到指定位置的节点
for (int i = 0; i < index - 1; i++) {
currentNode = currentNode.next;
}
// 让添加节点的下一个节点为指定位置的节点
addNode.next = currentNode;
// 让指定位置节点的上一个节点的下一个节点为添加节点,即在指定位置插入添加节点
currentNode.prev.next = addNode;
// 再让添加节点的上一个节点为指定位置节点的上一个节点
addNode.prev = currentNode.prev;
// 再让指定位置的上一个节点为添加节点
currentNode.prev = addNode;
length ++;
}
}
测试类:
public class DoubleLinkNodeTest {
public static void main(String[] args) throws Exception {
DoubleLinkNode<Object> doubleLinkNode = new DoubleLinkNode<>();
doubleLinkNode.addFirst("张三"); // 张三
doubleLinkNode.addFirst(1); // 1 张三
doubleLinkNode.queryAll();
doubleLinkNode.addLast("李四"); // 1 张三 李四
doubleLinkNode.queryAll();
doubleLinkNode.addIndex("王五", 3); // 1 张三 王五 李四
doubleLinkNode.queryAll();
System.out.println("长度:" + doubleLinkNode.getLength());
}
}
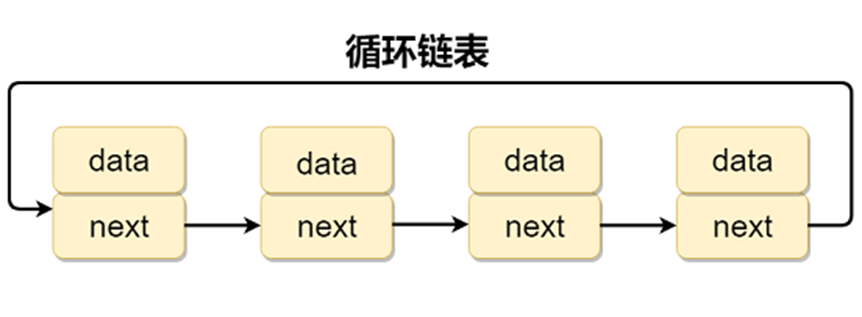
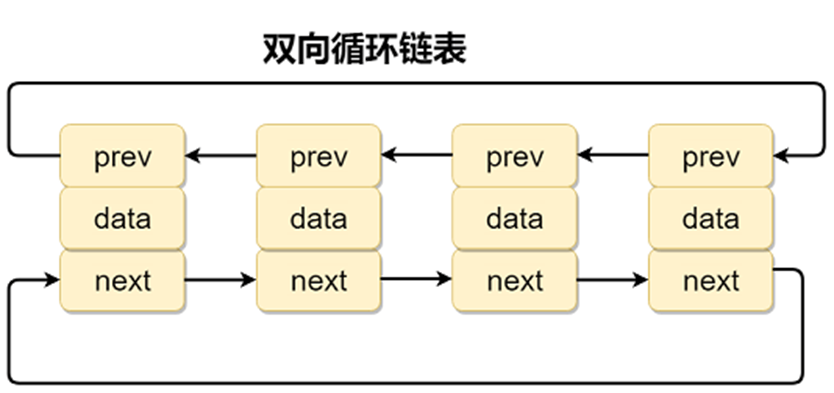
1.3 循环列表与双向循环列表
只需把单链表与双向链表的尾结点的下一个节点指向头结点即可
1.4 应用场景与数组比较
1.4.1 应用场景
- 如果需要支持随机访问的话,链表没办法做到
- 如果需要存储的数据元素的个数不确定,并且需要经常添加和删除数据的话,使用链表比较合适
- 如果需要存储的数据元素的个数确定,并且不需要经常添加和删除数据的话,使用数组比较合适
1.4.2 与数组比较
- 数组支持随机访问,而链表不支持
- 数组使用的是连续内存空间对 CPU 的缓存机制友好,链表则相反
- 数组的大小固定,而链表则天然支持动态扩容。如果声明的数组过小,需要另外申请一个更大的内存空间存放数组元素,然后将原数组拷贝进去,这个操作是比较耗时的
2. 栈
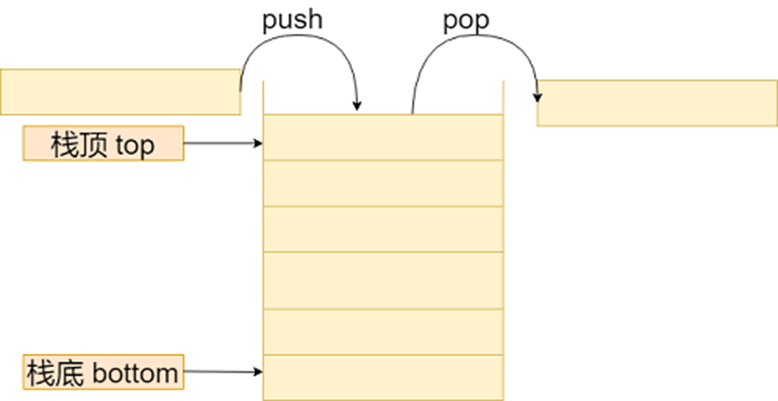
栈 (stack)只允许在有序的线性数据集合的一端(称为栈顶 top)进行加入数据(push)和移除数据(pop)。因而按照 后进先出(LIFO, Last In First Out) 的原理运作。在栈中,push 和 pop 的操作都发生在栈顶
栈常用一维数组或链表来实现,用数组实现的栈叫作 数组栈(顺序栈),用链表实现的栈叫作 链式栈。其时间复杂度为:
- 访问:O(n)最坏情况
- 插入删除:O(1)顶端插入和删除元素
2.1 数组栈
public class MyStack<T> {
private T[] storage; // 存放栈中元素的数组
private int capacity; // 栈的容量
private int count; // 栈中元素数量
private static final int GROW_FACTOR = 2; // 扩容倍数
// 无参构造方法。默认容量为 8
public MyStack(){
capacity = 8;
storage = (T[]) new Object[8];
count = 0;
}
// 带初始容量的构造方法
public MyStack(int initialCapacity){
if (initialCapacity < 1) {
throw new IllegalArgumentException("Capacity too small.");
}
capacity = initialCapacity;
storage = (T[]) new Object[initialCapacity];
count = 0;
}
// 入栈
public void push(T val){
if (count == capacity){
expansion();
}
storage[count++] = val;
}
// 扩容,使用 Arrays.copyOf() 复制原数组并扩容
public void expansion(){
int newCapacity = capacity * GROW_FACTOR;
storage = Arrays.copyOf(storage, newCapacity);
capacity = newCapacity;
}
// 返回栈顶元素并出栈
public T pop(){
if (count == 0) {
throw new IllegalArgumentException("Stack is empty.");
}
return storage[--count];
}
// 返回栈顶元素不出栈
public T peek(){
if (count == 0){
throw new IllegalArgumentException("Stack is empty.");
} else {
return storage[count - 1];
}
}
// 判断栈是否为空
public boolean isEmpty(){
return count == 0;
}
// 返回栈中元素的个数
public int size(){
return count;
}
}
测试类:
public static void main(String[] args) {
MyStack myStack = new MyStack(3);
myStack.push(1);
myStack.push("张三");
myStack.push(2);
myStack.push("李四");
System.out.println(myStack.peek()); // 李四
System.out.println(myStack.isEmpty()); // false
System.out.println(myStack.size()); // 4
for (int i = 0; i < 4; i++) {
System.out.println(myStack.pop());
}
}

2.2 链栈
与链表实现类似,入栈即使用头插法插入,出栈即把头结点指向下一个节点
定义节点类:
@NoArgsConstructor
@AllArgsConstructor
public class Node<T> {
T val; // 节点值
public Node next; // 指向后续节点
Node(T val) {
this.val = val;
}
}
操作类:
public class LinkStack<T> {
private Node head;
private int length;
public LinkStack(){
head = new Node();
length = 0;
}
// 清空
public void clear(){
head.next = null;
head.val = null;
length = 0;
}
// 入栈,头插法
public void push(T val){
Node addNode = new Node<>(val);
if (head.val == null){
head = addNode;
} else {
addNode.next = head;
head = addNode;
}
length ++;
}
// 出栈,将头结点指向下一个,并返回值
public T pop(){
T val = (T) head.val;
head = head.next;
length --;
return val;
}
public int getLength(){
return length;
}
public T peek(){
return (T) head.val;
}
public void queryAll(){
Node currentNode = head;
while (currentNode != null){
System.out.println(currentNode.val);
currentNode = currentNode.next;
}
}
}
测试类:
public static void main(String[] args) {
LinkStack<Object> linkStack = new LinkStack<>();
linkStack.push("张三");
linkStack.push(1);
linkStack.push(2);
linkStack.pop();
System.out.println("栈顶元素:" + linkStack.peek());
System.out.println("链表长度:" + linkStack.getLength());
linkStack.queryAll();
}
2.3 应用场景
当要处理的数据只涉及在一端插入和删除数据,并且满足 后进先出(LIFO, Last In First Out) 的特性时,就可以使用栈这个数据结构
2.3.1 实现浏览器的回退和前进功能
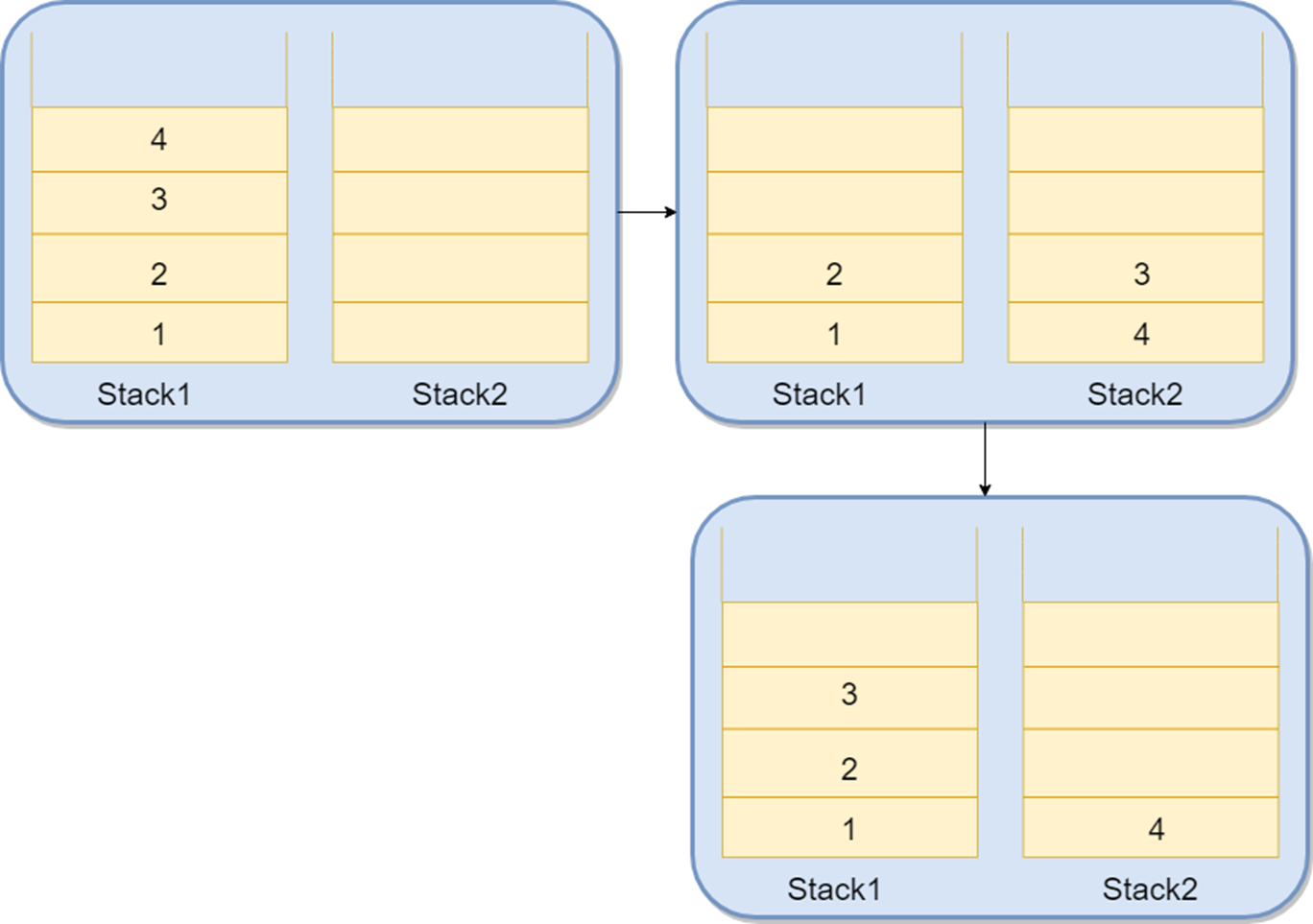
只需要使用两个栈(Stack1 和 Stack2)就能实现这个功能。比如按顺序查看了 1,2,3,4 这四个页面,依次把 1,2,3,4 这四个页面压入 Stack1 中。当想回头看 2 这个页面的时候,点击回退按钮,依次把 4,3 这两个页面从 Stack1 弹出,然后压入 Stack2 中。假如又想回到页面 3,你点击前进按钮,将 3 页面从 Stack2 弹出,然后压入到 Stack1 中
2.3.2 检查符号是否成对出现
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断该字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。
比如 "()"、"()[]{}"、"{[]}" 都是有效字符串,而 "(]" 、"([)]" 则不是。
首先将括号间的对应规则存放在 Map 中。然后将字符串转为数组进行遍历,假如是左符号,就直接压入栈中;右符号则将栈顶元素出栈进行比较。因为栈是后入先出,刚好可以与成对符号进行匹配。判断左右符号则由 Map 的 Key,Value 进行判断,Key 为右符号,Value 为左符号
public boolean isValid(String s){
// 括号之间的对应规则
HashMap<Character, Character> mappings = new HashMap<Character, Character>();
mappings.put(')', '(');
mappings.put('}', '{');
mappings.put(']', '[');
Stack<Character> stack = new Stack<Character>();
char[] chars = s.toCharArray();
for (int i = 0; i < chars.length; i++) {
if (mappings.containsKey(chars[i])) {
char topElement = stack.empty() ? '#' : stack.pop();
if (topElement != mappings.get(chars[i])) {
return false;
}
} else {
stack.push(chars[i]);
}
}
return stack.isEmpty();
}
2.3.3 反转字符串
先压栈再出栈即可
2.3.4 维护函数调用
最后一个被调用的函数必须先完成执行,符合栈的 后进先出(LIFO, Last In First Out) 特性
3. 队列
队列 是 先进先出( FIFO,First In, First Out) 的线性表。在具体应用中通常用链表或者数组来实现,用数组实现的队列叫作 顺序队列 ,用链表实现的队列叫作 链式队列 。队列只允许在后端(rear)进行插入操作也就是 入队 enqueue,在前端(front)进行删除操作也就是出队 dequeue
队列的操作方式和堆栈类似,唯一的区别在于队列只允许新数据在后端进行添加

3.1 单队列
单队列就是常见的队列, 每次添加元素时,都是添加到队尾。单队列又分为 顺序队列(数组实现) 和 链式队列(链表实现)
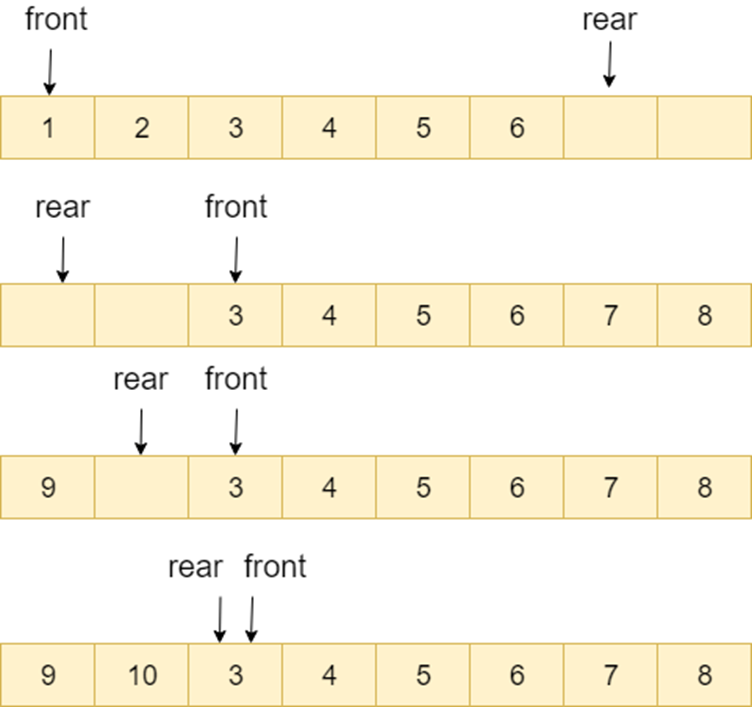
顺序队列存在“假溢出”的问题也就是明明有位置却不能添加的情况
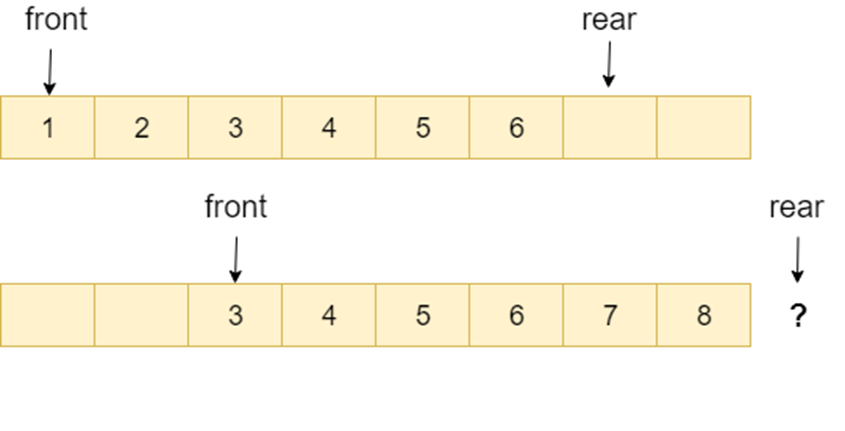
上图是一个顺序队列,将前两个元素 1,2 出队,并入队两个元素 7,8。当进行入队、出队操作的时候,front 和 rear 都会持续往后移动,当 rear 移动到最后的时候,无法再往队列中添加数据,即使数组中还有空余空间,这种现象就是 ”假溢出“ 。除了假溢出问题之外,如下图所示,当添加元素 8 的时候,rear 指针移动到数组之外(越界)
为了避免当只有一个元素的时候,队头和队尾重合使处理变得麻烦,所以引入两个指针,front 指针指向对头元素,rear 指针指向队列最后一个元素的下一个位置,这样当 front 等于 rear 时,此队列不是还剩一个元素,而是空队列
3.1.1 数组单队列
只能使用一次
public class ArrayQueue<T> {
private T[] storage; // 存放队列元素的数组
private int front; // 队列头
private int rear; // 队列尾
private int maxsize; // 队列最大容量
// 无参构造,默认大小为8
public ArrayQueue(){
storage = (T[]) new Object[8];
front = -1;
rear = -1;
maxsize = 8;
}
// 带初始大小的构造方法
public ArrayQueue(int size){
storage = (T[]) new Object[size];
front = -1;
rear = -1;
maxsize = size;
}
// 判断是否队列已满
public boolean isFull(){
return rear == maxsize - 1;
}
// 判断队列是否为空
public boolean isEmpty(){
return front == rear;
}
// 入队
public void enqueue(T val){
if (isFull()){
throw new ArrayIndexOutOfBoundsException("队列已满");
}
storage[++rear] = val;
}
// 遍历队列
public void queryQueue(){
if (isEmpty()){
System.out.println("队列为空");
return;
}
for (int i = 0; i < storage.length; i++) {
if (storage[i] != null){
System.out.print(storage[i] + " ");
}
}
System.out.println();
}
// 出队
public T dequeue(){
if (isEmpty()){
throw new ArrayIndexOutOfBoundsException("队列为空");
}
T result = storage[++front];
storage[front] = null;
return result;
}
// 获取队列头元素
public T peek(){
if (isEmpty()){
throw new ArrayIndexOutOfBoundsException("队列为空");
}
return storage[front + 1];
}
}
测试类:
public class Demo{
public static void main(String[] args) {
ArrayQueue<Object> arrayQueue = new ArrayQueue<>();
arrayQueue.enqueue(1); // 1
arrayQueue.enqueue("张三"); // 张三 1
arrayQueue.enqueue(2); // 2 张三 1
arrayQueue.enqueue("李四"); // 李四 2 张三 1
System.out.println("队列是否已满:" + arrayQueue.isFull()); // false
System.out.println("出队元素:" + arrayQueue.dequeue());
System.out.println("出队元素:" + arrayQueue.dequeue());
System.out.println("获取队头元素不出队:" + arrayQueue.peek());
arrayQueue.queryQueue();
System.out.println("出队元素:" + arrayQueue.dequeue());
System.out.println("出队元素:" + arrayQueue.dequeue());
System.out.println("队列是否为空:" + arrayQueue.isEmpty());
}
}
3.1.2 链式单队列
- 插入元素时:每次直接插到末尾即可(尾插法),新插入的元素即为新的尾结点(区别于栈的头插法)
- 取出元素时:返回首结点指向的下一个元素即可。(先进先出),此时和弹栈一样
队列为尾插头取,栈为头插头取
public class LinkQueue<T> {
private Node head;
private Node last;
private int length;
public LinkQueue() {
length = 0;
}
// 判断队列是否为空
public boolean isEmpty() {
return length == 0;
}
// 入队
public void enqueue(T val) {
Node node = new Node(val);
if (isEmpty()) {
head = node;
last = node;
} else {
last.next = node;
}
last = node;
length++;
}
// 遍历队列
public void queryQueue() {
Node currentNode = head;
while (currentNode != null) {
System.out.print(currentNode.val + " ");
currentNode = currentNode.next;
}
System.out.println();
}
// 出队
public T dequeue() {
if (isEmpty()) {
return null;
}
T val = (T) head.val;
head = head.next;
length--;
return val;
}
// 获取队列长度
public int getLength() {
return length;
}
// 获取队列头元素
public T getHead() {
if (isEmpty()) {
return null;
}
return (T) head.val;
}
// 获取队列尾元素
public T getLast() {
if (isEmpty()) {
return null;
}
return (T) last.val;
}
}
测试类:
public class Demo05{
public static void main(String[] args) {
LinkQueue<Object> linkQueue = new LinkQueue<>();
linkQueue.enqueue(1); // 1
linkQueue.enqueue("张三"); // 张三 1
linkQueue.enqueue(2); // 2 张三 1
linkQueue.enqueue("李四"); // 李四 2 张三 1
System.out.println("出队元素:" + linkQueue.dequeue()); // 1
System.out.println("队头元素:" + linkQueue.getHead()); // 张三
System.out.println("队尾元素:" + linkQueue.getLast()); // 李四
System.out.println("出队元素:" + linkQueue.dequeue()); // 张三
linkQueue.queryQueue();
System.out.println("队列长度:" + linkQueue.getLength()); // 2
}
}
3.2 循环队列
循环队列可以解决顺序队列的假溢出和越界问题。解决办法就是:从头开始,这样也就会形成头尾相接的循环,这也就是循环队列名字的由来。将 rear 指针指向数组下标为 0 的位置就不会有越界问题了。当再向队列中添加元素的时候, rear 向后移动
顺序队列中,front == rear 的时候队列为空,循环队列中则不一样,也可能为满,如上图所示。解决办法有两种:
- 可以设置一个标志变量 flag,当
front == rear并且 flag=0 的时候队列为空,当front == rear并且 flag=1 的时候队列为满 - 队列为空的时候就是
front == rear,队列满的时候,保证数组还有一个空闲的位置,rear 就指向这个空闲位置,如下图所示,那么现在判断队列是否为满的条件就是:(rear+1) % QueueSize= front

3.2.1 数组循环队列
- front 变量的含义做一个调整:front 指向队列的第一个元素,也就是说 arr[front] 就是队列的第一个元素,front 的初始值=0
- rear 变量的含义做一个调整:rear 指向队列的最后一个元素的后一个位置,因为希望空出一个位置来进行判断,rear 的初始值=0
- 当队列满时,条件是
(rear +1) % maxSize = front【满】 - 对队列为空的条件,
rear == front 空 - 队列中有效的数据的个数
(rear + maxSize -front) % maxSize
public class CircularQueue<T> {
private T[] storage; // 存放队列元素的数组
private int front; // 队列头
private int rear; // 队列尾
private int maxsize; // 队列最大容量
// 无参构造,默认大小为8
public CircularQueue(){
storage = (T[]) new Object[8];
maxsize = 8;
// front = 0; 指向第一个元素,默认是0可以不写
// rear = 0; 指向最后一个元素的下一位,默认是0可以不写
}
// 带初始大小的构造方法
public CircularQueue(int size){
storage = (T[]) new Object[size];
maxsize = size;
// front = 0; 指向第一个元素,默认是0可以不写
// rear = 0; 指向最后一个元素的下一位,默认是0可以不写
}
// 判断是否队列已满
public boolean isFull(){
return (rear + 1) % maxsize == front;
}
// 判断队列是否为空
public boolean isEmpty(){
return front == rear;
}
// 入队
public void enqueue(T val){
if (isFull()){
throw new ArrayIndexOutOfBoundsException("队列已满");
}
storage[rear] = val;
rear = (rear + 1) % maxsize;
}
// 求出当前有效数据
public int getEffectiveSize(){
return (rear + maxsize - front) % maxsize;
}
//遍历
public void queryQueue() {
if (isEmpty()) {
System.out.println("队列为空");
return;
}
for (int i = front; i < front + getEffectiveSize(); i++) {
System.out.print(storage[i % maxsize] + " ");
}
System.out.println();
}
// 出队
public T dequeue(){
if (isEmpty()){
throw new ArrayIndexOutOfBoundsException("队列为空");
}
T val = storage[front];
storage[front] = null;
front = (front + 1) % maxsize;
return val;
}
// 取队首元素
public T getFront(){
if (isEmpty()){
throw new ArrayIndexOutOfBoundsException("队列为空");
}
return storage[front];
}
// 取队尾元素
public T getRear(){
if (isEmpty()){
throw new ArrayIndexOutOfBoundsException("队列为空");
}
return storage[(rear - 1 + maxsize) % maxsize];
}
}
测试类:
public class Demo{
public static void main(String[] args) {
CircularQueue<Object> circularQueue = new CircularQueue<>(4);
circularQueue.enqueue(1); // 1
circularQueue.enqueue("张三"); // 张三 1
circularQueue.enqueue("李四"); // 李四 张三 1
System.out.println("出队元素:" + circularQueue.dequeue());
System.out.println("队头元素:" + circularQueue.getFront());
System.out.println("出队元素:" + circularQueue.dequeue());
circularQueue.queryQueue();
circularQueue.enqueue("王五"); // 王五 李四
circularQueue.enqueue("赵六"); // 赵六 王五 李四
circularQueue.queryQueue();
System.out.println("队尾元素:" + circularQueue.getRear());
}
}
3.2.2 链式循环队列
在链式单队列的基础上,让尾结点的 next 指向头结点即可
3.3 常见应用场景
- 阻塞队列: 阻塞队列可以看成在队列基础上加了阻塞操作的队列。当队列为空的时候,出队操作阻塞,当队列满的时候,入队操作阻塞。使用阻塞队列我们可以很容易实现 “生产者 - 消费者“ 模型
- 线程池中的请求 / 任务队列: 当线程池中没有空闲线程时,新的任务请求线程资源时,将这些请求放在队列中,当有空闲线程的时候,会循环中反复从队列中获取任务来执行。队列分为无界队列(基于链表)和有界队列(基于数组)。无界队列的特点就是可以一直入列,除非系统资源耗尽,比如 :
FixedThreadPool使用无界队列LinkedBlockingQueue。但是有界队列就不一样了,当队列满的话后面再有任务/请求就会拒绝,在 Java 中的体现就是会抛出java.util.concurrent.RejectedExecutionException异常 - Linux 内核进程队列(按优先级排队)
- 播放器上的播放列表
- 消息队列
- 等等......
4. 树
树就是一种类似现实生活中的树的数据结构(倒置的树)。任何一颗非空树只有一个根节点。一棵树具有以下特点:
- 一棵树中的任意两个结点有且仅有唯一的一条路径连通
- 一棵树如果有 n 个结点,那么它一定恰好有 n-1 条边
- 一棵树不包含回路
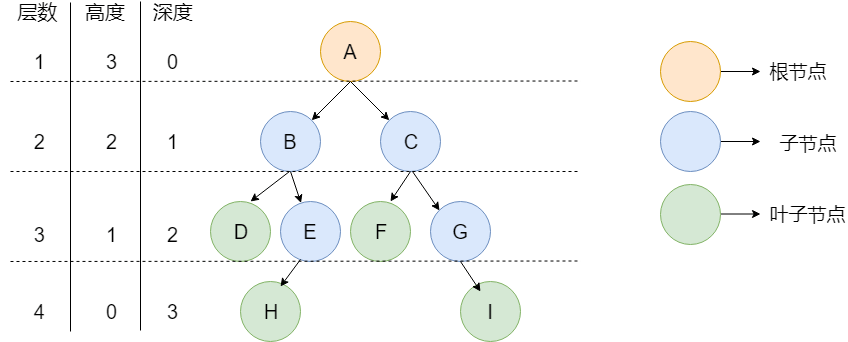
树中的常用概念:
- 节点 :树中的每个元素都可以统称为节点。
- 根节点 :顶层节点或者说没有父节点的节点。上图中 A 节点就是根节点。
- 父节点 :若一个节点含有子节点,则这个节点称为其子节点的父节点。上图中的 B 节点是 D 节点、E 节点的父节点。
- 子节点 :一个节点含有的子树的根节点称为该节点的子节点。上图中 D 节点、E 节点是 B 节点的子节点。
- 兄弟节点 :具有相同父节点的节点互称为兄弟节点。上图中 D 节点、E 节点的共同父节点是 B 节点,故 D 和 E 为兄弟节点。
- 叶子节点 :没有子节点的节点。上图中的 D、F、H、I 都是叶子节点。
- 节点的高度 :该节点到叶子节点的最长路径所包含的边数。
- 节点的深度 :根节点到该节点的路径所包含的边数
- 节点的层数 :节点的深度+1。
- 树的高度 :根节点的高度
4.1 二叉树的分类
- 二叉树(Binary tree)是每个节点最多只有两个分支(即不存在分支度大于 2 的节点)的树结构
- 二叉树 的分支通常被称作 “左子树” 或 “右子树”。并且,二叉树 的分支具有左右次序,不能随意颠倒
- 二叉树 的第 i 层至多拥有
2^(i-1)个节点,深度为 k 的二叉树至多总共有2^(k+1) - 1个节点(满二叉树的情况),至少有2^(k)个节点
4.1.1 满二叉树
一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是 满二叉树。也就是说,如果一个二叉树的层数为 K,且结点总数是 (2^k) -1 ,则它就是 满二叉树。如下图所示:
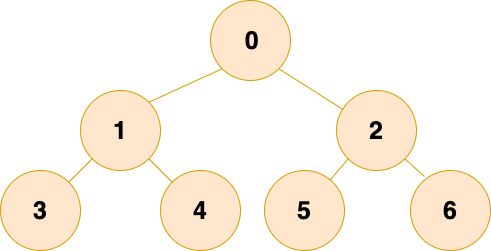
4.1.2 完全二叉树
除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则这个二叉树就是 完全二叉树 。
即一棵树从根结点开始扩展,扩展完左子节点才能开始扩展右子节点,每扩展完一层,才能继续扩展下一层。如下图所示:
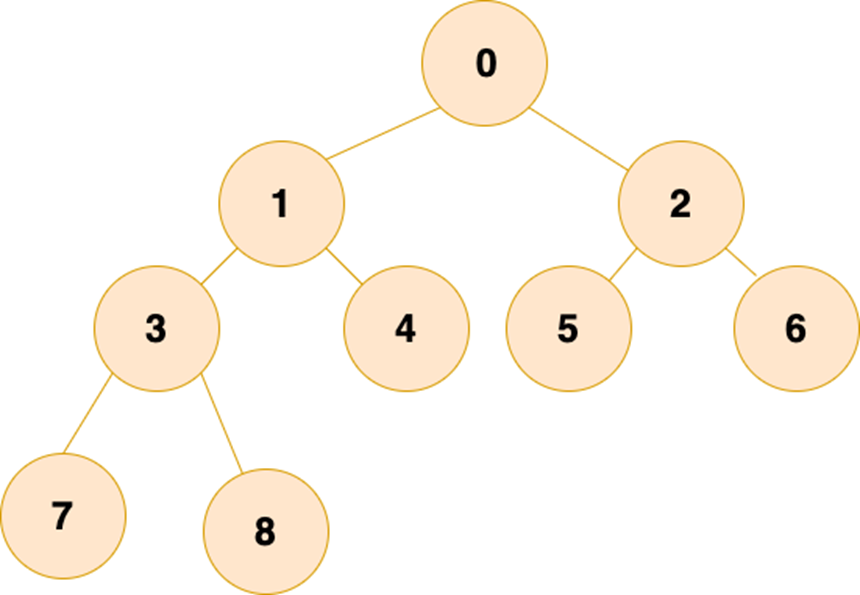
完全二叉树有一个很好的性质:父结点和子节点的序号有着对应关系
当根节点的值为 1 的情况下,若父结点的序号是 i,那么左子节点的序号就是 2i,右子节点的序号是 2i+1。这个性质使得完全二叉树利用数组存储时可以极大地节省空间,以及利用序号找到某个节点的父结点和子节点
4.1.3 二叉排序树
一棵空树,或者是具有下列性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值
- 若右子树不空,则右子树上所有结点的值均大于它的根结点的值
- 左、右子树也分别为二叉排序树
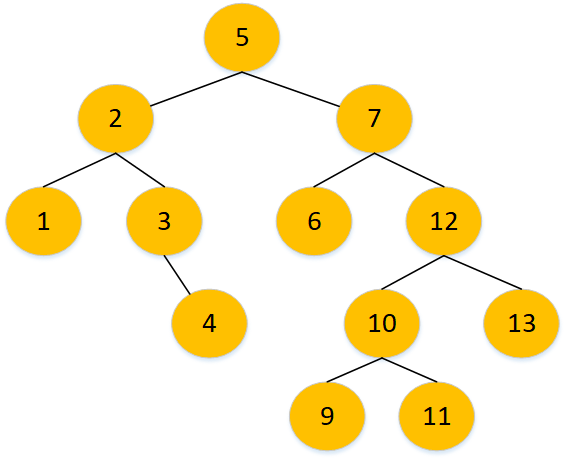
1. 查找 Find
- 查找的值 x 从根节点开始
- 如果 x 小于根节点的值,则在左子树中继续查找
- 如果 x 大于根节点的值,则在右子树中继续查找
- 如果x等于根节点的值则返回该节点
- 查不到就返回 null
查找的效率决定于树的高度,最大元素在树的最右支的节点,最小元素在树的最左支的节点上
2. 插入 Insert
- 插入的值从根节点开始查找
- 如果 x 小于根节点的值,则在左子树中继续查找
- 如果 x 大于根节点的值,则在右子树中继续查找
- 如果该节点是叶节点,x 小于该节点值则插入左子节点,否则插入右节点
3. 删除 delete,删除节点分为3类
- 无儿子节点的节点,也就是叶子结点(删除节点分为左叶子节点和右叶子节点)
找到要删除的节点及其父节点,然后判断删除节点是父节点的左节点还是右节点,再将对应的删除节点置为 null
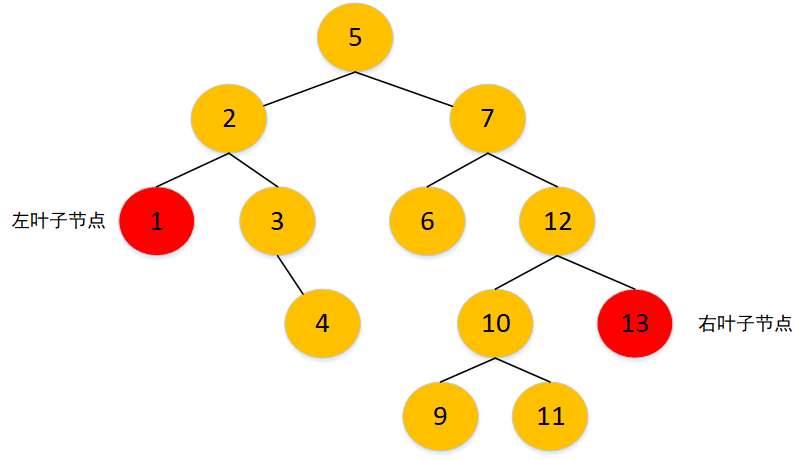
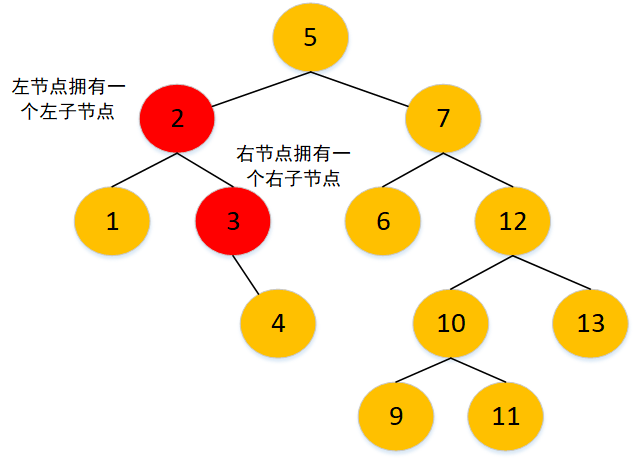
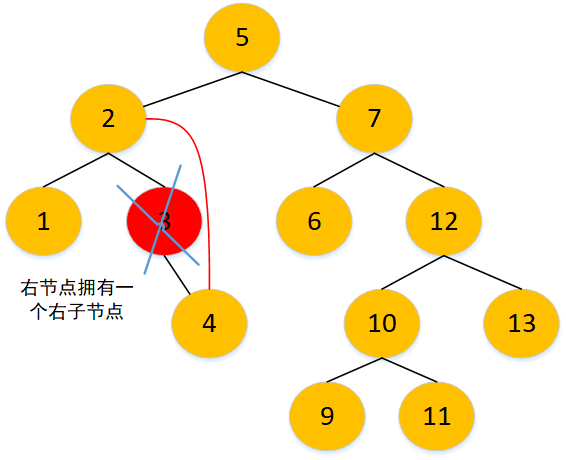
- 只有一个儿子的节点(删除节点分为只有一个左子节点或只有一个右子节点,同时删除节点也分为左节点和右节点)
找到要删除的节点及其父节点,判断删除节点拥有左子节点还是右子节点,再判断删除节点是父节点的左节点还是右节点,再将父亲节点链接删除节点的子节点,相当于删除要删除的节点
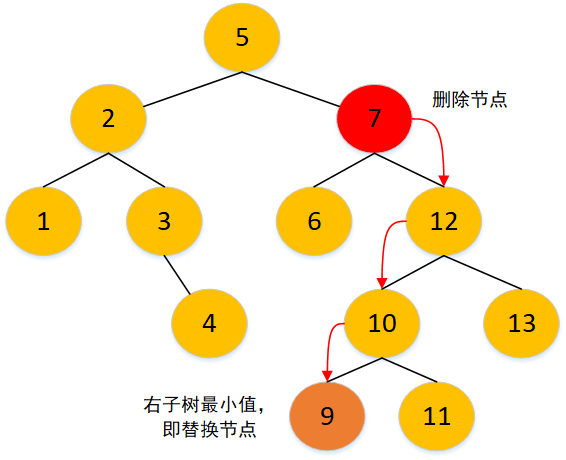
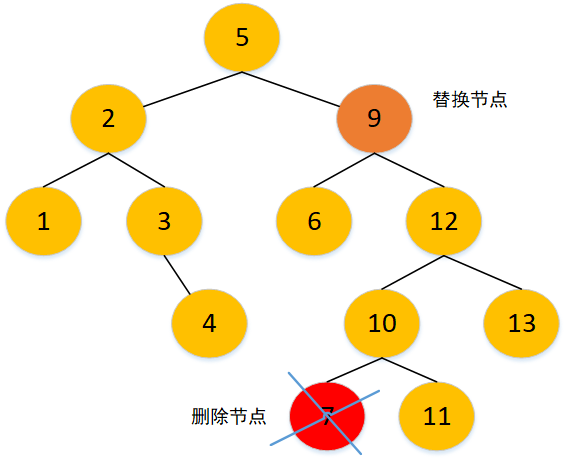
- 有两个儿子的节点(应考虑用哪个节点替换该节点的位置,并保证新的树也是个二叉排序树)
找到删除节点,再找到其右子树的最小值,即删除节点的右子节点的最左子节点,其为替换节点,同时找到替换节点的父节点,然后将删除节点与替换节点进行替换,再删掉替换节点,即置为 null。假如没有最左子节点,删除节点的右子节点就是替换节点
定义树节点:
@Data
public class TreeNode {
public Integer data;
public TreeNode leftChild;
public TreeNode rightChild;
public TreeNode(Integer data) {
this.data = data;
}
}
二叉排序树操作类:
public class BinarySortedTree {
public TreeNode root;
// 非递归构建二叉排序树
public void insert(int val) {
TreeNode addTreeNode = new TreeNode(val);
if (root == null) {
root = addTreeNode;
} else {
TreeNode currentTreeNode = root;
TreeNode parentTreeNode;
while (true) {
parentTreeNode = currentTreeNode;
if (addTreeNode.data > currentTreeNode.data) {
currentTreeNode = currentTreeNode.rightChild;
if (currentTreeNode == null) {
parentTreeNode.rightChild = addTreeNode;
return;
}
} else {
currentTreeNode = currentTreeNode.leftChild;
if (currentTreeNode == null) {
parentTreeNode.leftChild = addTreeNode;
return;
}
}
}
}
}
// 递归构建二叉排序树
public TreeNode insert(TreeNode treeNode, int val) {
TreeNode addTreeNode = new TreeNode(val);
if (root == null) {
return root = addTreeNode;
}
if (val > treeNode.data) {
if (treeNode.rightChild == null) {
treeNode.rightChild = addTreeNode;
return root;
}
return insert(treeNode.rightChild, val);
} else {
if (treeNode.leftChild == null) {
treeNode.leftChild = addTreeNode;
return root;
}
return insert(treeNode.leftChild, val);
}
}
// 先序遍历二叉排序树
public void preOrder(TreeNode treeNode) {
if (treeNode == null) {
return;
}
System.out.print(treeNode.data + " ");
preOrder(treeNode.leftChild);
preOrder(treeNode.rightChild);
}
// 中序遍历二叉排序树
public void inOrder(TreeNode treeNode) {
if (treeNode == null) {
return;
}
inOrder(treeNode.leftChild);
System.out.print(treeNode.data + " ");
inOrder(treeNode.rightChild);
}
// 后序遍历二叉排序树
public void postOrder(TreeNode treeNode) {
if (treeNode == null) {
return;
}
postOrder(treeNode.leftChild);
postOrder(treeNode.rightChild);
System.out.print(treeNode.data + " ");
}
// 层序遍历二叉排序树
public void levelOrder(TreeNode treeNode) {
if (treeNode == null) {
return;
}
LinkedList<TreeNode> linkedList = new LinkedList<>();
linkedList.offer(treeNode);
TreeNode currentTreeNode;
while (!linkedList.isEmpty()) {
currentTreeNode = linkedList.poll();
System.out.print(currentTreeNode.data + " ");
if (currentTreeNode.leftChild != null) {
linkedList.offer(currentTreeNode.leftChild);
}
if (currentTreeNode.rightChild != null) {
linkedList.offer(currentTreeNode.rightChild);
}
}
System.out.println();
}
// 查找元素是否在二叉排序树中,如果在返回该节点,否则返回null
public TreeNode find(int val) {
TreeNode currentTreeNode = root;
while (currentTreeNode != null) {
if (currentTreeNode.data == val) {
return currentTreeNode;
} else if (currentTreeNode.data > val) {
currentTreeNode = currentTreeNode.leftChild;
} else {
currentTreeNode = currentTreeNode.rightChild;
}
}
return null;
}
// 查找二叉排序树中最小值
public int findMin() {
TreeNode deleteTreeNode = root;
while (deleteTreeNode.leftChild != null) {
deleteTreeNode = deleteTreeNode.leftChild;
}
return deleteTreeNode.data;
}
// 删除节点
public void delete(int val) {
TreeNode deleteTreeNode = root;
TreeNode parentTreeNode = root;
// 找到要删除的节点
while (deleteTreeNode.data != val) {
parentTreeNode = deleteTreeNode;
if (deleteTreeNode.data > val) {
deleteTreeNode = deleteTreeNode.leftChild;
} else {
deleteTreeNode = deleteTreeNode.rightChild;
}
if (deleteTreeNode == null) {
break;
}
}
if (deleteTreeNode != null) {
if (deleteTreeNode.leftChild == null && deleteTreeNode.rightChild == null) { // 叶子节点
if (deleteTreeNode == root) {
root = null;
} else if (parentTreeNode.leftChild == deleteTreeNode) { // 左子节点
parentTreeNode.leftChild = null;
} else { // 右子节点
parentTreeNode.rightChild = null;
}
} else if (deleteTreeNode.leftChild == null) { // 只有一个右子节点
if (deleteTreeNode == root) {
root = deleteTreeNode.rightChild;
} else if (parentTreeNode.leftChild == deleteTreeNode) { // 左子节点
parentTreeNode.leftChild = deleteTreeNode.rightChild;
} else { // 右子节点
parentTreeNode.rightChild = deleteTreeNode.rightChild;
}
} else if (deleteTreeNode.rightChild == null) { // 只有一个左子节点
if (deleteTreeNode == root) {
root = deleteTreeNode.leftChild;
} else if (parentTreeNode.leftChild == deleteTreeNode) { // 左子节点
parentTreeNode.leftChild = deleteTreeNode.leftChild;
} else { // 右子节点
parentTreeNode.rightChild = deleteTreeNode.leftChild;
}
} else { // 有两个子节点
// 先定义一个 替换节点 保存要删除节点的右子树的最小值
TreeNode replaceTreeNode = deleteTreeNode.rightChild;
// 定义一个 替换节点的父节点 保存要删除节点的右子树的最小值的父节点
TreeNode replaceParentTreeNode = deleteTreeNode;
// 找到删除节点的右节点的最左子节点,即右子树的最小值
while (replaceTreeNode.leftChild != null) {
// 将其赋值给 替换节点的父节点
replaceParentTreeNode = replaceTreeNode;
// 将其 左节点 赋值给替换节点
replaceTreeNode = replaceTreeNode.leftChild;
}
// 将替换节点的值赋值给要删除节点
deleteTreeNode.data = replaceTreeNode.data;
// 如果替换节点的父节点的左节点是替换节点,则将替换节点的右节点赋值给替换节点的父节点的左节点
// 即有最左子节点的情况
if (replaceParentTreeNode.leftChild == replaceTreeNode) {
replaceParentTreeNode.leftChild = replaceTreeNode.rightChild;
} else {
// 如果替换节点的父节点的右节点是替换节点,则将替换节点的右节点赋值给替换节点的父节点的右节点
// 即没有左子节点的情况,删除节点的右子节点就是替换节点,同时其并没有左子节点,所以使用替换节点的右节点
replaceParentTreeNode.rightChild = replaceTreeNode.rightChild;
}
}
} else {
System.out.println("要删除的节点不存在!");
}
}
}
测试类:
public class Demo {
public static void main(String[] args) {
BinarySortedTree binarySortedTree = new BinarySortedTree();
// binarySortedTree.insert(binarySortedTree.root, 1);
binarySortedTree.insert(5);
binarySortedTree.insert(7);
binarySortedTree.insert(2);
binarySortedTree.insert(1);
binarySortedTree.insert(3);
binarySortedTree.insert(4);
binarySortedTree.insert(6);
binarySortedTree.insert(12);
binarySortedTree.insert(10);
binarySortedTree.insert(9);
binarySortedTree.insert(11);
binarySortedTree.insert(13);
System.out.print("先序遍历:");
binarySortedTree.preOrder(binarySortedTree.root); // 5 2 4 8
System.out.println();
System.out.print("中序遍历:");
binarySortedTree.inOrder(binarySortedTree.root); // 2 4 5 8
System.out.println();
System.out.print("后序遍历:");
binarySortedTree.postOrder(binarySortedTree.root); // 1 4 2 6 9 8 5
System.out.println();
System.out.print("层次遍历:");
binarySortedTree.levelOrder(binarySortedTree.root); // 5 2 8 1 4 6 9
System.out.println("查找值【3】对应的节点:" + binarySortedTree.find(3));
binarySortedTree.delete(7);
System.out.print("删除值【7】后的二叉排序树:");
binarySortedTree.levelOrder(binarySortedTree.root);
}
}

4.1.4 平衡二叉树
平衡二叉树 是一棵二叉排序树,且具有以下性质:
- 可以是一棵空树
- 如果不是空树,它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树(左右高度差小于等于 1)
平衡二叉树的常用实现方法有:红黑树、AVL 树、替罪羊树、加权平衡树、伸展树 等
如下这棵树已经退化为一个链表了,管它叫 斜树
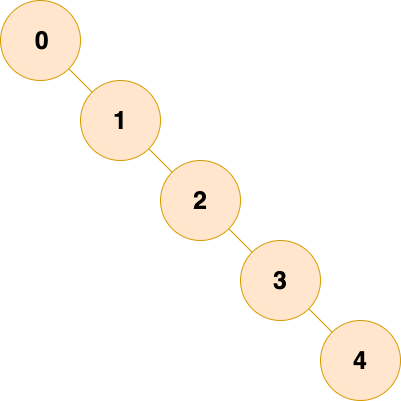
二叉树相比于链表,由于父子节点以及兄弟节点之间往往具有某种特殊的关系,这种关系使得在树中对数据进行搜索和修改时,相对于链表更加快捷便利
但是,如果二叉树退化为一个链表了,那么那么树所具有的优秀性质就难以表现出来,效率也会大打折,为了避免这样的情况,希望每个父结点分给左儿子和分给右儿子的尽可能一样多,相差最多不超过一层,如下图所示:
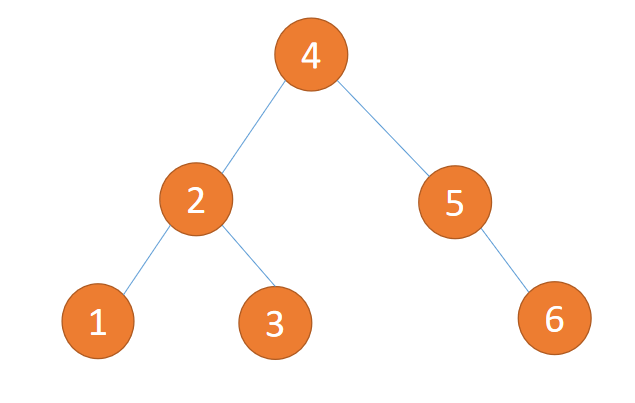
4.2 二叉树的存储
二叉树的存储主要分为 链式存储 和 顺序存储 两种
4.2.1 顺序存储
顺序存储就是利用数组进行存储,数组中的每一个位置仅存储节点的 data,不存储左右子节点的指针,子节点的索引通过数组下标完成
根结点的序号为 1,对于每个节点 Node,假设它存储在数组中下标为 i 的位置,那么它的左子节点就存储在 2i 的位置,它的右子节点存储在下标为 2i+1 的位置
一棵完全二叉树的数组顺序存储如下图所示:
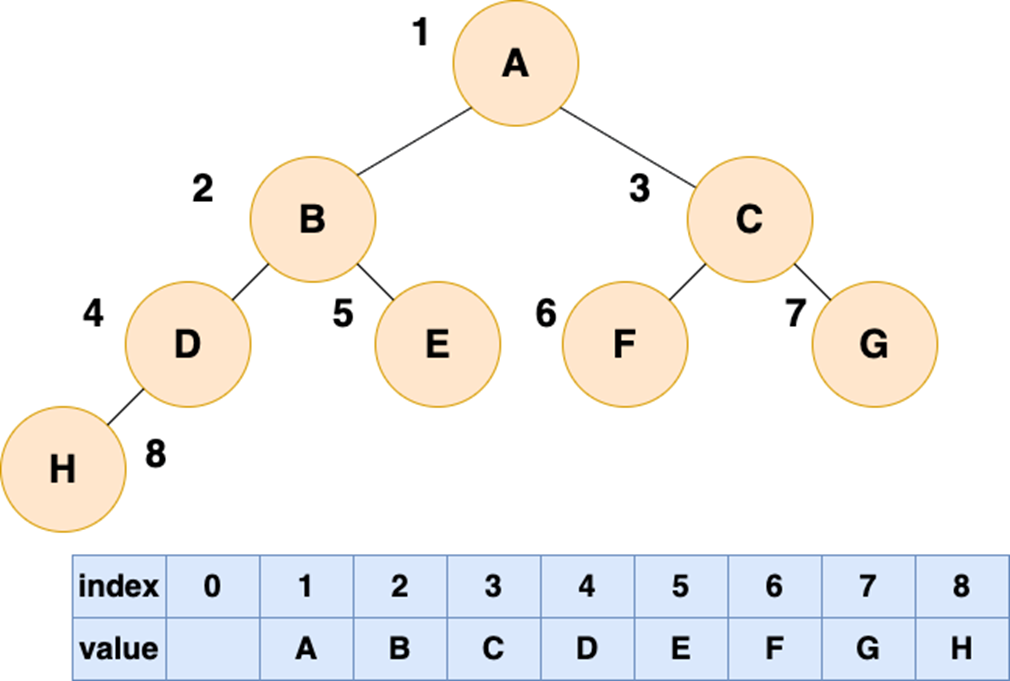
如果存储的二叉树不是完全二叉树,在数组中就会出现空隙,导致内存利用率降低
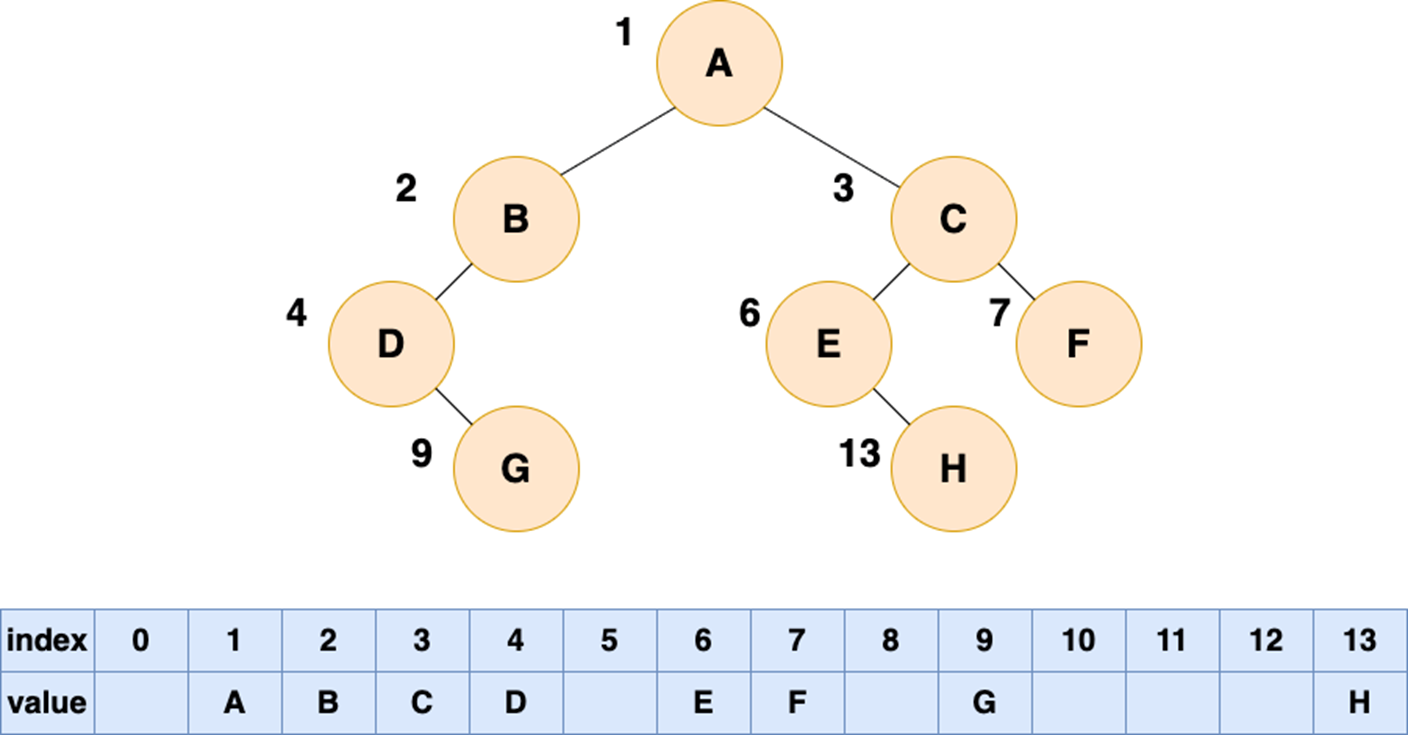
简单实现
public class ArrayTree {
private int[] storage;
public ArrayTree(){
storage = new int[8];
}
public ArrayTree(int length){
storage = new int[length];
}
// 添加根节点
public void addRoot(int val){
storage[1] = val;
}
// 添加左子节点
public void addLeft(int index, int val){
if(index > storage.length || index < 0){
throw new IndexOutOfBoundsException();
}
storage[2 * index] = val;
}
// 添加右子节点
public void addRight(int index, int val){
storage[ 2 * index + 1] = val;
}
// 获取一个节点的父节点
public int getParent(int index){
if(index > storage.length || index < 0){
throw new IndexOutOfBoundsException();
}
return storage[index / 2];
}
// 遍历
public void query(){
for(int i = 1; i < storage.length; i++){
System.out.print(storage[i] + " ");
}
System.out.println();
}
}
测试类:
public class Demo05 {
public static void main(String[] args) {
ArrayTree arrayTree = new ArrayTree(10);
arrayTree.addRoot(1);
arrayTree.addLeft(1, 2);
arrayTree.addRight(1, 3);
arrayTree.addLeft(2, 4);
arrayTree.addLeft(4, 5);
arrayTree.query();
System.out.println(arrayTree.getParent(8));
}
}
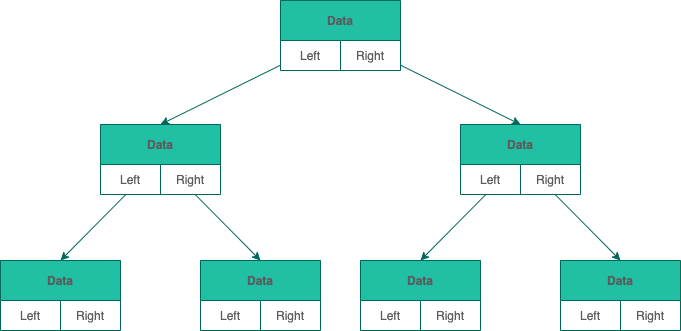
4.2.2 链式存储
和链表类似,二叉树的链式存储依靠指针将各个节点串联起来,不需要连续的存储空间。每个节点包括三个属性:
- 数据 data。data 不一定是单一的数据,根据不同情况,可以是多个具有不同类型的数据
- 左节点指针 left
- 右节点指针 right
4.3 二叉树的遍历
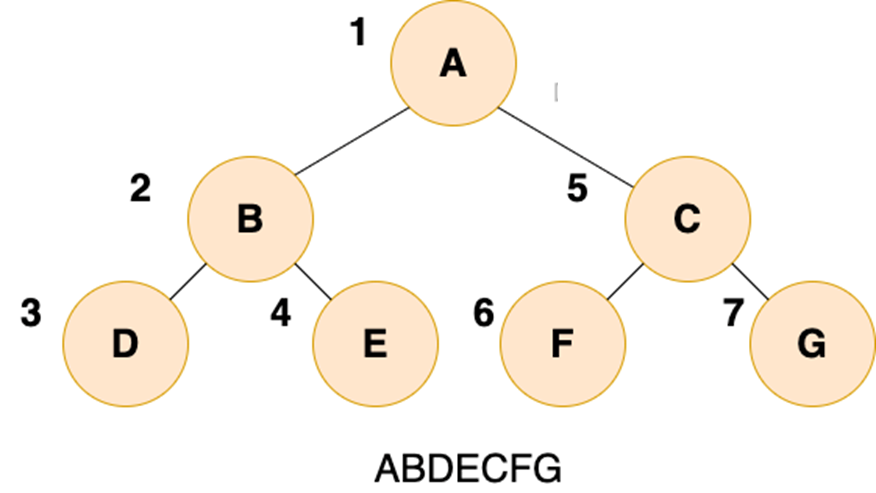
4.3.1 先序遍历
二叉树的先序遍历,就是先输出根结点,再遍历左子树,最后遍历右子树,遍历左子树和右子树的时候,同样遵循先序遍历的规则,也就是说,可以递归实现先序遍历
public void preOrder(TreeNode treeNode) {
if (treeNode == null) {
return;
}
System.out.print(treeNode.data + " ");
preOrder(treeNode.leftChild);
preOrder(treeNode.rightChild);
}
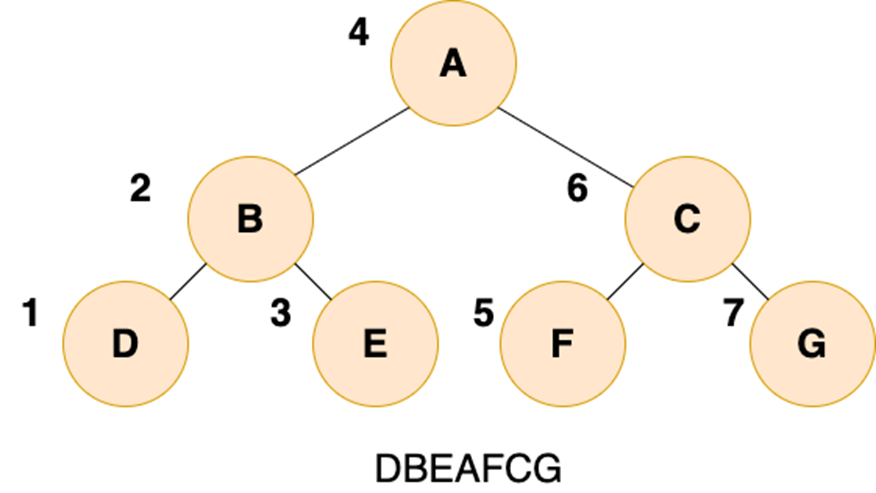
4.3.2 中序遍历
二叉树的中序遍历,就是先递归中序遍历左子树,再输出根结点的值,再递归中序遍历右子树,可以想象成一巴掌把树压扁,父结点被拍到了左子节点和右子节点的中间,如下图所示:

public void inOrder(TreeNode root){
if(root == null){
return;
}
inOrder(root.left);
system.out.println(root.data);
inOrder(root.right);
}
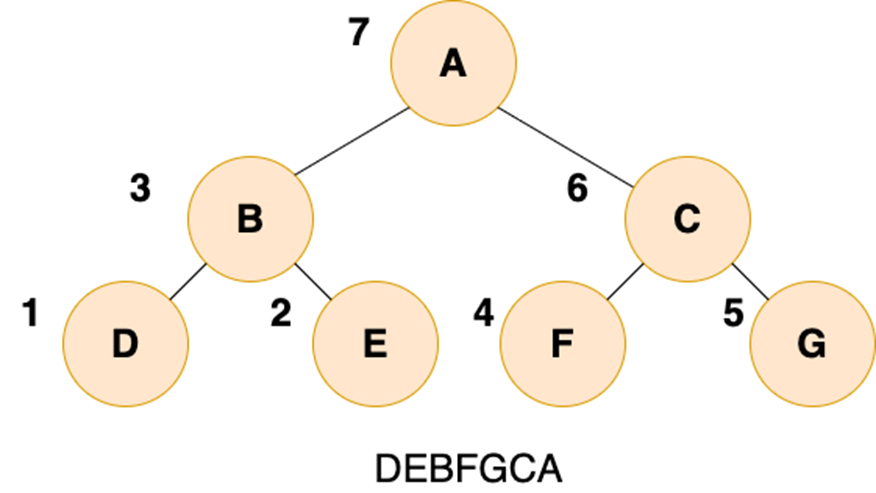
4.3.3 后序遍历
二叉树的后序遍历,就是先递归后序遍历左子树,再递归后序遍历右子树,最后输出根结点的值
public void postOrder(TreeNode root){
if(root == null){
return;
}
postOrder(root.left);
postOrder(root.right);
system.out.println(root.data);
}
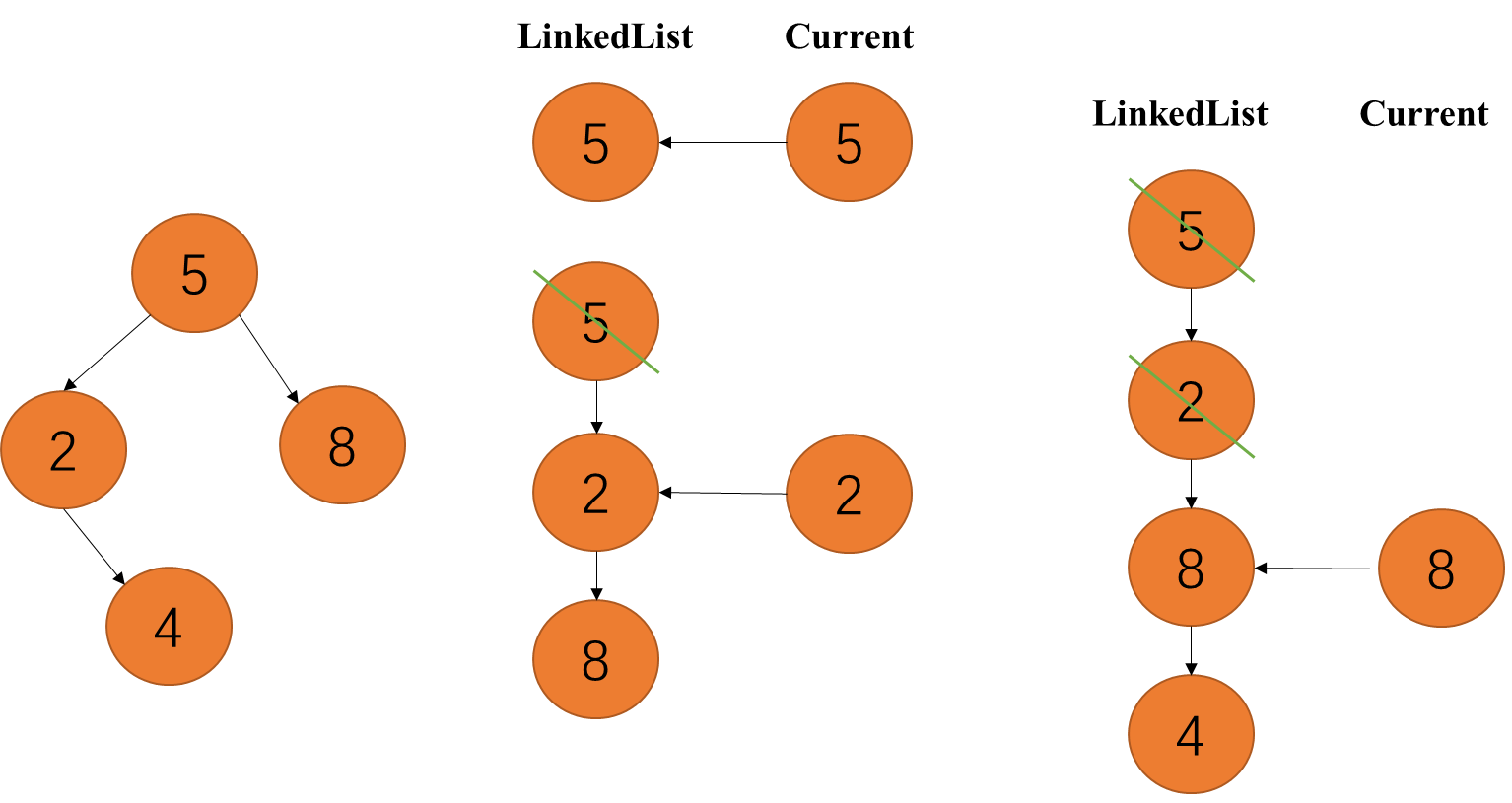
4.3.4 层次遍历
即一层一层往下遍历。使用链表,先将根节点加到链表中,然后再将根节点的左节点和右节点加入到链表中,这里定义一个 Current 节点,用来将左右节点加入到链表里以及遍历链表,这里用 poll 方式来给 Current 节点赋值
public void levelOrder(TreeNode treeNode) {
if (treeNode == null) {
return;
}
LinkedList<TreeNode> linkedList = new LinkedList<>();
linkedList.offer(treeNode);
TreeNode currentTreeNode;
while (!linkedList.isEmpty()) {
currentTreeNode = linkedList.poll();
System.out.print(currentTreeNode.data + " ");
if (currentTreeNode.leftChild != null) {
linkedList.offer(currentTreeNode.leftChild);
}
if (currentTreeNode.rightChild != null) {
linkedList.offer(currentTreeNode.rightChild);
}
}
System.out.println();
}
4.4 哈夫曼树(最优⼆叉树)
4.4.1 概述
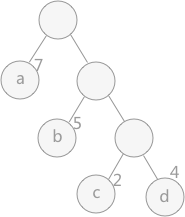
- 路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。如下图中,从根结点到结点 a 之间的通路就是一条路径
- 路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。下图中从根结点到结点 c 的路径长度为 3
- 结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。例如,下图 中结点 a 的权为 7,结点 b 的权为 5
- 结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如,下图中结点 b 的带权路径长度为 2 * 5 = 10
- 树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如下图中所示的这颗树的带权路径长度为:
WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3
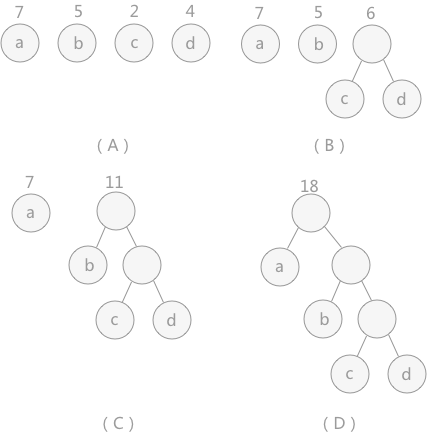
当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为 “最优二叉树”,有时也叫 “赫夫曼树” 或者 “哈夫曼树”
在构建哈弗曼树时,要使树的带权路径长度最小,只需要遵循一个原则,那就是:权重越大的结点离树根越近。在上图中,因为结点 a 的权值最大,所以理应直接作为根结点的孩子结点。
构建方法:
- 在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和
- 在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推
- 重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树
4.4.2 实现
定义节点类:
public class TreeNode<T> {
public T data;
public int weight;
public TreeNode<T> leftChild;
public TreeNode<T> rightChild;
public TreeNode(T data, int weight) {
this.data = data;
this.weight = weight;
}
public String toString(){
return data + " " + weight;
}
}
哈夫曼树构建:
public class HuffmanTree {
// 构建Huffman树
public <T> TreeNode<T> buildHuffmanTree(List<TreeNode> treeNodes) {
while (treeNodes.size() > 1){
sortTreeNode(treeNodes);
// 左边比右边小
TreeNode left = treeNodes.get(0);
TreeNode right = treeNodes.get(1);
// 生成一个新的节点,父结点权重为两个子结点之和
TreeNode parent = new TreeNode(null, left.weight + right.weight);
// 让子结点与父结点连接
parent.leftChild = left;
parent.rightChild = right;
// 删除最小的
treeNodes.remove(0);
// 删除第二小的
treeNodes.remove(0);
// 把新的父结点加入到 list 中
treeNodes.add(parent);
}
// 返回哈夫曼树的根节点
return treeNodes.get(0);
}
// 对节点进行排序,从小到大
public void sortTreeNode(List<TreeNode> treeNodes) {
for (int i = 0; i < treeNodes.size(); i++){
for (int j = 0; j < treeNodes.size() - 1 - i; j++){
if (treeNodes.get(j).weight > treeNodes.get(j + 1).weight) {
TreeNode temp = treeNodes.get(j + 1);
treeNodes.set(j+1,treeNodes.get(j));
treeNodes.set(j,temp);
}
}
}
}
// 打印哈夫曼树
public void printTree(TreeNode root) {
System.out.println("Node-" + root.toString());
if(root.leftChild != null){
System.out.print("left:");
printTree(root.leftChild);
}
if(root.rightChild !=null){
System.out.print("right:");
printTree(root.rightChild);
}
}
}
测试类:
public class Demo {
public static void main(String[] args) {
HuffmanTree huffmanTree = new HuffmanTree();
List<TreeNode> treeNodes = new ArrayList<TreeNode>();
//把节点加入至list中
treeNodes.add(new TreeNode("张三", 10));
treeNodes.add(new TreeNode(1, 15));
treeNodes.add(new TreeNode("李四", 12));
treeNodes.add(new TreeNode(2, 3));
treeNodes.add(new TreeNode("王五", 4));
treeNodes.add(new TreeNode(3, 13));
treeNodes.add(new TreeNode("赵六", 1));
// 进行哈夫曼树的构造
TreeNode root = huffmanTree.buildHuffmanTree(treeNodes);
// 打印哈夫曼树
huffmanTree.printTree(root);
}
}
4.5 AVL 树
4.5.1 概述
AVL 树是严格的平衡二叉树,平衡条件必须满足(所有节点的左右子树高度差的绝对值不超过1),一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡。不管是插入还是删除操作,只要不满足上面的条件,就要通过旋转来保持平衡,而旋转是非常耗时的,由此 AVL 树适合用于插入与删除次数比较少,但查找多的情况
由于维护这种高度平衡所付出的代价比从中获得的效率收益还大,故而实际的应用不多,更多的地方是用追求局部而不是非常严格整体平衡的红黑树。如果应用场景中对插入删除不频繁,只是对查找要求较高,那么 AVL 还是较优于红黑树(AVL 树查找比红黑树快)
二叉平衡树的调整:调整原则根据插入的节点和失衡节点的位置上关系来划分
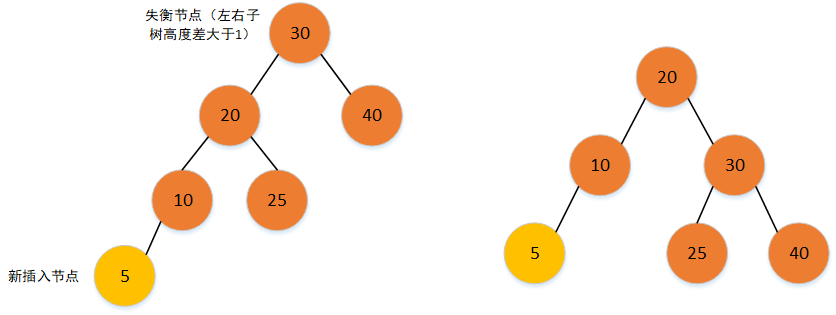
- LL旋转,让失衡节点的左子节点成为新节点,让新节点的右子节点成为失衡节点的左子节点,再让失衡节点成为新节点的右子节点

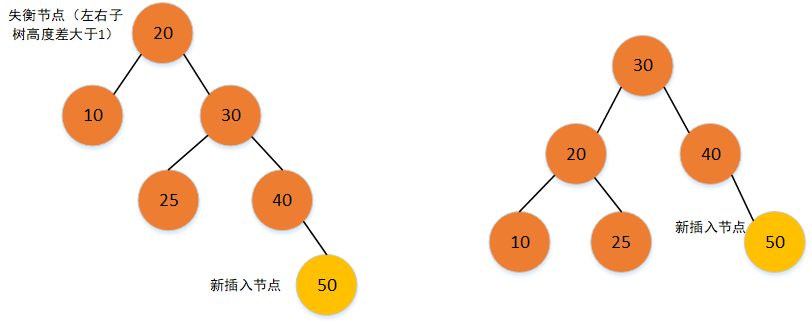
- RR旋转,让失衡节点的右子节点成为新节点,让新节点的左子节点成为失衡节点的右子节点,再让失衡节点成为新节点的左子节点

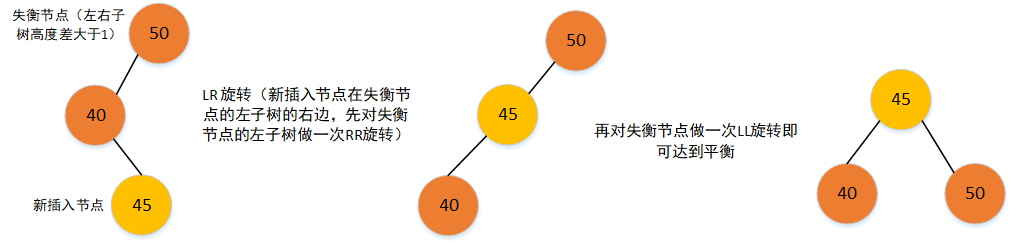
- LR旋转,对失衡节点的左子树做一次RR旋转,再对失衡节点做一次LL旋转
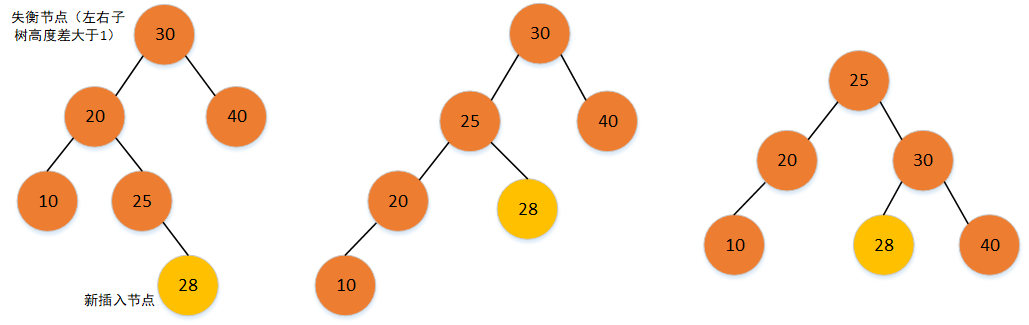
- RL旋转
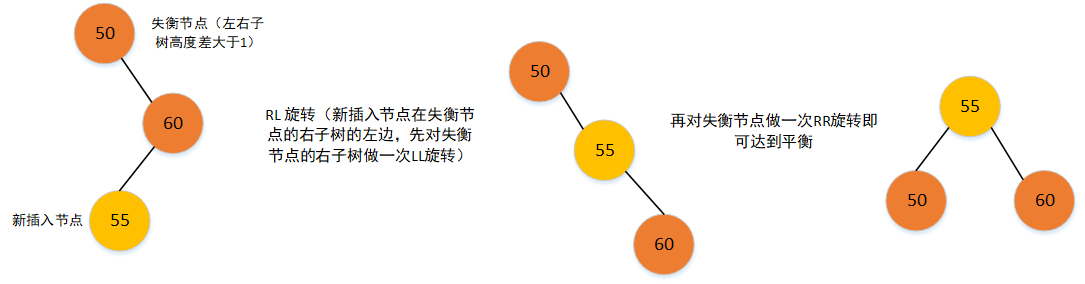
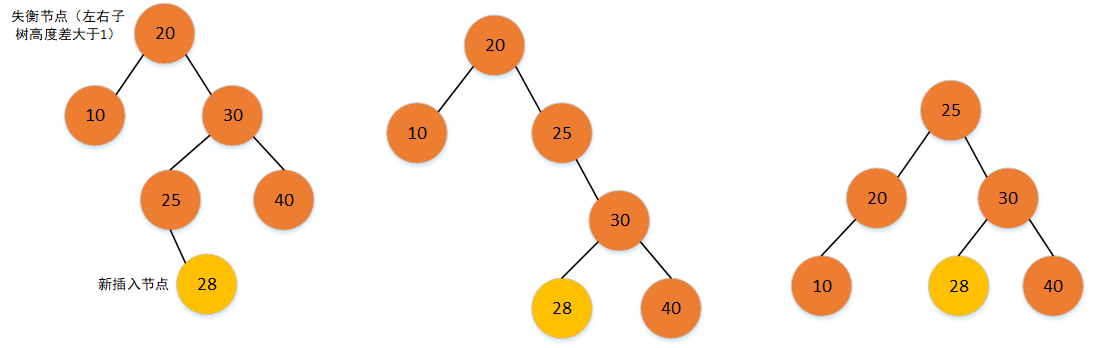
4.5.2 实现
节点类
public class AVLTreeNode {
Integer data; // 数据
AVLTreeNode leftChild; // 左子节点
AVLTreeNode rightChild; // 右子节点
int height; // 记录该节点所在的高度
public AVLTreeNode(int data) {
this.data = data;
}
}
AVL树实现类
public class AVLTree {
public AVLTreeNode root;
private int size;
public AVLTree() {
this.root = null;
this.size = 0;
}
public int getSize(){
return size;
}
// 获取节点的高度,让空节点高度为-1
public int getHeight(AVLTreeNode avlTreeNode) {
return avlTreeNode == null ? -1 : avlTreeNode.height;
}
// 先序遍历
public void printTree(AVLTreeNode root) {
System.out.print(root.data + " ");
if(root.leftChild != null){
printTree(root.leftChild);
}
if(root.rightChild != null){
printTree(root.rightChild);
}
}
// 插入节点
public AVLTreeNode insert(AVLTreeNode avlTreeNode, int val) {
if (avlTreeNode == null){
avlTreeNode = new AVLTreeNode(val);
size ++;
return avlTreeNode;
}
if (val < avlTreeNode.data) {
// 如果插入的值小于当前节点的值,则插入到左子树中
avlTreeNode.leftChild = insert(avlTreeNode.leftChild, val);
// 如果左子树与右子树的高度差大于1,则需要进行平衡调整,这里使用左子树的高度减右子树的高度,节点为空高度为-1
if (getHeight(avlTreeNode.leftChild) - getHeight(avlTreeNode.rightChild) > 1) {
// 如果插入的值小于当前节点(即失衡节点)的左子节点的值,即插入的节点在失衡节点的左子节点的左边,则进行LL型旋转
if (val < avlTreeNode.leftChild.data) {
System.out.println("LL型旋转");
avlTreeNode = LLRotate(avlTreeNode);
} else { // 如果插入的值不小于当前节点(即失衡节点)的左子节点的值,即插入的节点在失衡节点的左子节点的右边,则进行LR型旋转
System.out.println("LR型旋转");
avlTreeNode = LRRotate(avlTreeNode);
}
}
} else { // 如果插入的值不小于当前节点的值,则插入到右子树中
avlTreeNode.rightChild = insert(avlTreeNode.rightChild, val);
// 平衡调整
if (getHeight(avlTreeNode.rightChild) - getHeight(avlTreeNode.leftChild) > 1){
// 如果插入的值小于等于当前节点(即失衡节点)的右子节点的值,即插入的节点在失衡节点的右子节点的左边,则进行RL型旋转
if (val < avlTreeNode.rightChild.data){
System.out.println("RL型旋转");
avlTreeNode = RLRotate(avlTreeNode);
} else { // 如果插入的值大于当前节点(即失衡节点)的右子节点的值,即插入的节点在失衡节点的右子节点的右边,则进行RR型旋转
System.out.println("RR型旋转");
avlTreeNode = RRRotate(avlTreeNode);
}
}
}
// 更新节点的高度,获取左子树与右子树的最大高度,叶子节点高度为0,再加1即为当前节点的高度
avlTreeNode.height = Math.max(getHeight(avlTreeNode.leftChild), getHeight(avlTreeNode.rightChild)) + 1;
return avlTreeNode;
}
/**
* LL旋转,30为失衡点(左右子树高度差大于1),对失衡点的左子树,即对结点20进行左旋
* 30 20
* / \ / \
* 20 40 10 30
* / \ --LL旋转-- / / \
* 10 25 5 25 40
* /
* 56
*/
private AVLTreeNode LLRotate(AVLTreeNode avlTreeNode) {
// 将失衡点(30)的左子节点 20 作为新节点
AVLTreeNode newRoot = avlTreeNode.leftChild;
// 将新节点(20)的右子节点 25 作为失衡点(30)的左子节点
avlTreeNode.leftChild = newRoot.rightChild;
// 失衡点(30)作为新节点(20)的右子节点
newRoot.rightChild = avlTreeNode;
// 更新失衡点和新根节点的高度
avlTreeNode.height = Math.max(getHeight(avlTreeNode.leftChild), getHeight(avlTreeNode.rightChild)) + 1;
newRoot.height = Math.max(getHeight(newRoot.leftChild), getHeight(newRoot.rightChild)) + 1;
// 新节点取代原失衡点
return newRoot;
}
/**
* RR旋转,20为失衡点(左右子树高度差大于1),对失衡点的右子树,即对结点30进行左旋
* 20 30
* / \ / \
* 10 30 20 40
* / \ --RR旋转-- / \ \
* 25 40 10 25 50
* \
* 50
*/
private AVLTreeNode RRRotate(AVLTreeNode avlTreeNode) {
// 将失衡点(20)的右子节点 30 作为新节点
AVLTreeNode newRoot = avlTreeNode.rightChild;
// 将新节点(30)的左子节点 25 作为失衡点(20)的右子节点
avlTreeNode.rightChild = newRoot.leftChild;
// 失衡点(20)作为新节点(30)的左子节点
newRoot.leftChild = avlTreeNode;
// 更新失衡点和新根节点的高度
avlTreeNode.height = Math.max(getHeight(avlTreeNode.leftChild), getHeight(avlTreeNode.rightChild)) + 1;
newRoot.height = Math.max(getHeight(newRoot.leftChild), getHeight(newRoot.rightChild)) + 1;
// 新节点取代原失衡点
return newRoot;
}
/**
* LR旋转,先将失衡点(30)的左子树(20)进行 RR 旋转,再将失衡点(30)进行 LL 旋转
* 30 30 25
* / \ / \ / \
* 20 40 25 40 20 30
* / \ --先RR旋转-- / \ --再LL旋转-- / / \
* 10 25 20 28 10 28 40
* \ /
* 28 10
*/
private AVLTreeNode LRRotate(AVLTreeNode avlTreeNode) {
// 将失衡点(30)的左子节点(20)进行 RR 旋转
avlTreeNode.leftChild = RRRotate(avlTreeNode.leftChild);
// 将失衡点(30)进行 LL 旋转,并返回新节点代替原失衡点
return LLRotate(avlTreeNode);
}
/**
* RL旋转,先将失衡点(20)的右子树(30)进行 LL 旋转,再将失衡点(20)进行 RR 旋转
* 20 20 25
* / \ / \ / \
* 10 30 10 25 20 30
* / \ --LL旋转-- \ --RR旋转-- / / \
* 25 40 30 10 28 40
* \ / \
* 28 28 40
*/
private AVLTreeNode RLRotate(AVLTreeNode avlTreeNode) {
// 将失衡点(20)的右子节点(30)进行 LL 旋转
avlTreeNode.rightChild = LLRotate(avlTreeNode.rightChild);
// 将失衡点(20)进行 RR 旋转,并返回新节点代替原失衡点
return RRRotate(avlTreeNode);
}
}
测试类
public class AVLTreeTest {
public static void main(String[] args) {
AVLTree avlTree = new AVLTree();
avlTree.root = avlTree.insert(avlTree.root, 20);
avlTree.root = avlTree.insert(avlTree.root, 10);
avlTree.root = avlTree.insert(avlTree.root, 30);
avlTree.root = avlTree.insert(avlTree.root, 25);
avlTree.root = avlTree.insert(avlTree.root, 40);
avlTree.printTree(avlTree.root);
System.out.println();
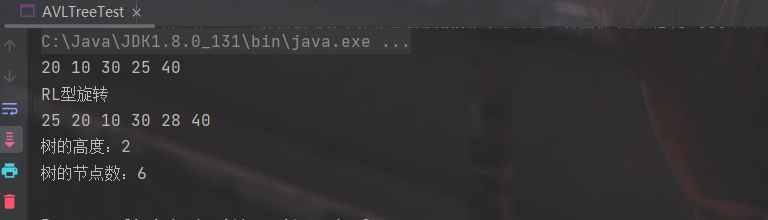
avlTree.root = avlTree.insert(avlTree.root, 28);
avlTree.printTree(avlTree.root);
System.out.println();
System.out.println("树的高度:" + avlTree.getHeight(avlTree.root));
System.out.println("树的节点数:" + avlTree.getSize());
}
}
4.6 红黑树
4.6.1 概述
- 节点非红即黑
- 根节点是黑色的
- 所有 Null 节点称为叶节点,且颜色为黑色
- 所有红色节点的子结点都是黑色,即从每个叶子到根的所有路径上不能有两个连续的红色结点
- 从任意节点到其叶节点的所有路径都包含相同数目的黑色节点
AVL 所有节点的左右子树高度差的绝对值不超过1,由于红黑树每个红色节点都必须有两个黑色的子节点,并且从任一节点到叶子节点的所有路径都包含相同数目的黑色节点,则红黑树最差情况下高度比是2:1
插入原则:假如插入节点的颜色为黑色的话,就破坏了红黑树的性质,所以每次插入的首先都是红节点。如果插入节点的父节点是黑色,能维持性质 。如果插入节点的父节点是红色,破坏了性质,需要通过重新着色或旋转,来维持性质
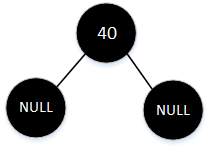
-
为根节点
根节点为空,则直接插入为根节点,颜色为黑色
-
插入节点的父结点为黑色
直接插入
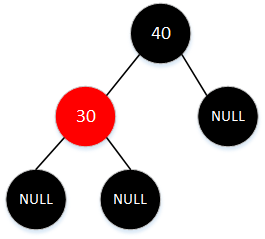
-
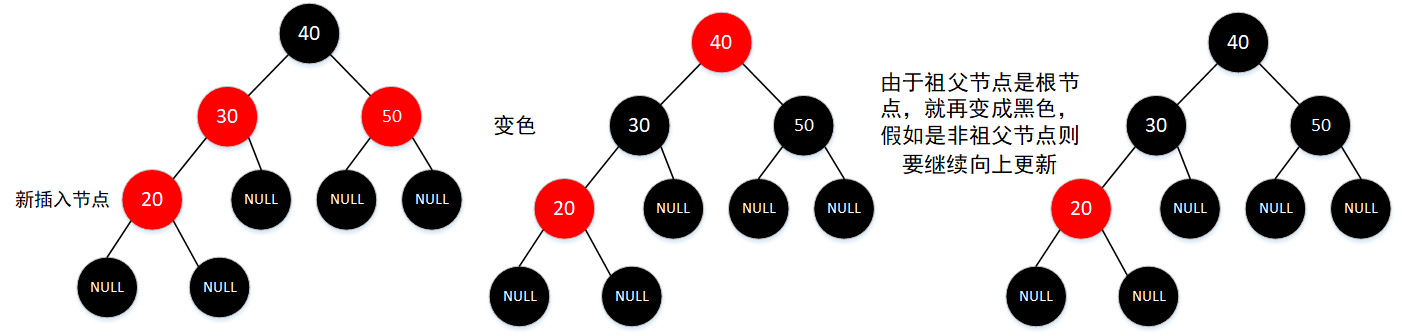
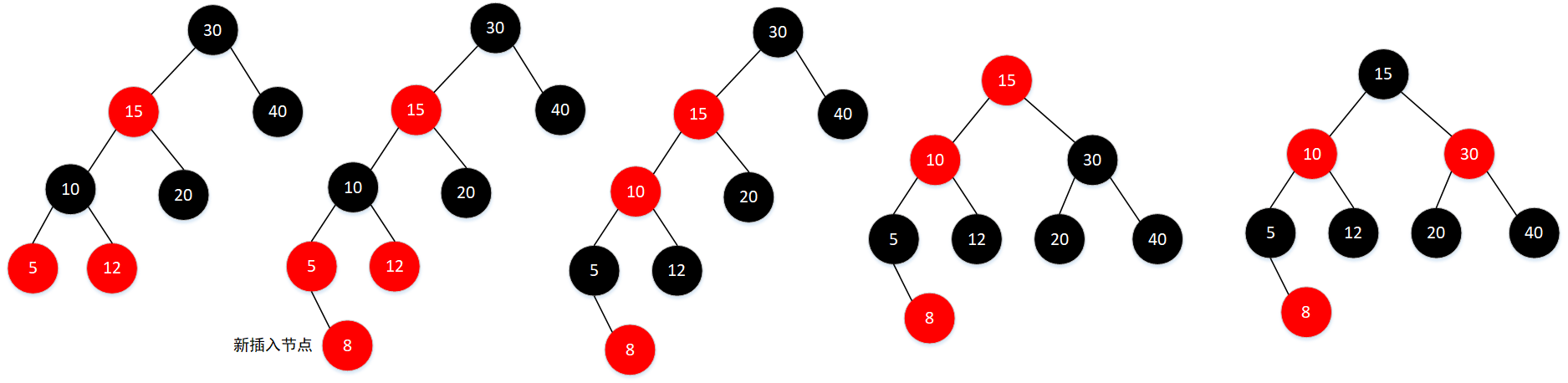
插入节点的父结点和叔父节点都是红色节点,先插入新节点(红色),插入节点的父结点、叔父节点和祖父节点都要变色。假如祖父节点为根节点,则变为黑色,否则继续向上更新
-
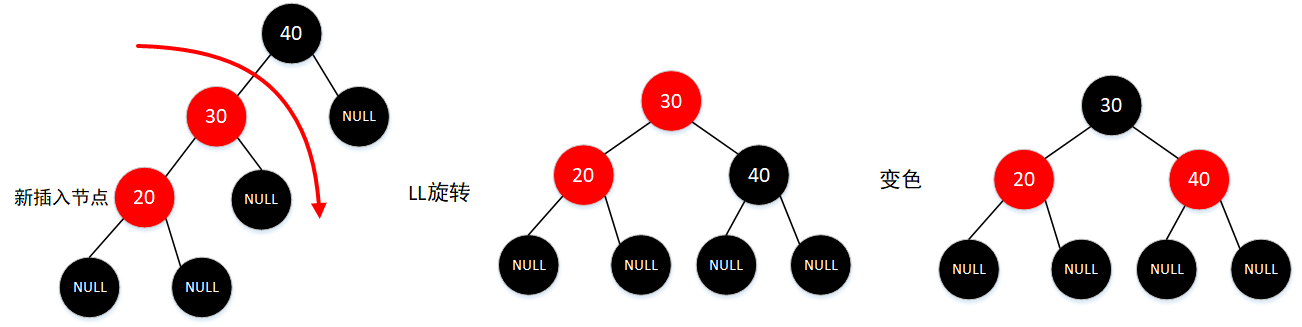
插入节点的父结点是红色,同时叔父节点是黑色,同时插入节点是其父结点的左子节点,而父结点是祖父节点的左子节点,这时要进行一次LL旋转调整插入节点和其父节点的角色(以父结点为轴)
这里由于旋转后根节点是红色所以进行了一次变色,为了满足红黑树的性质,叔父节点也进行一次变色
-
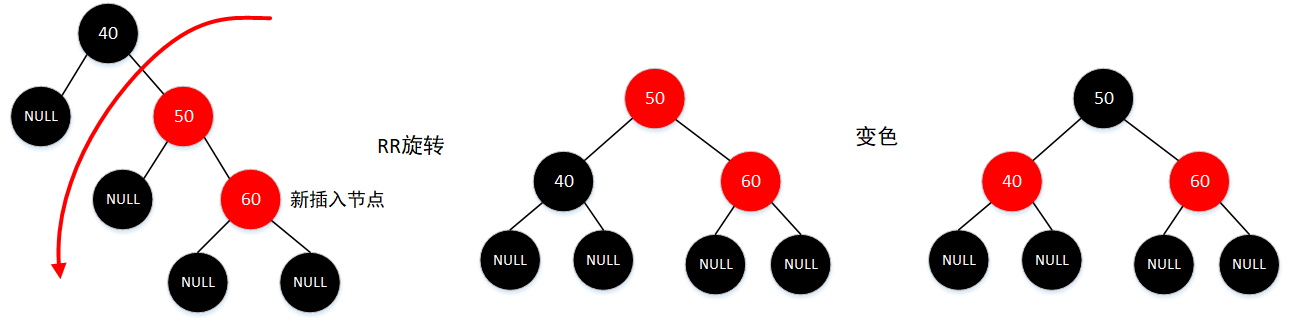
插入节点的父结点是红色,同时叔父节点都是黑色,同时插入节点是其父节点的右子节点,而父结点是祖父节点的右子节点,此时需要对祖父节点进行一次RR旋转(以父结点为轴),变色情况同 4
-
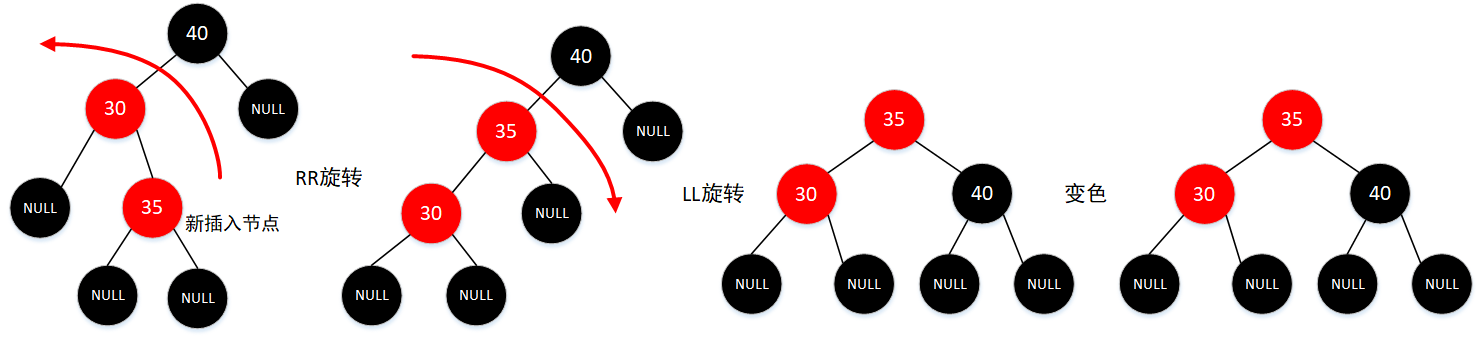
插入节点的父节点是红色,同时叔父节点都是黑色,同时插入节点是其父节点的右子节点,而父节点又是其父节点的左子节点(LR旋转)。先进行一次RR旋转调换新节点和其父节点的角色,旋转后发现节点符合情况 4,再进行一次LL旋转。变色情况同 4
-
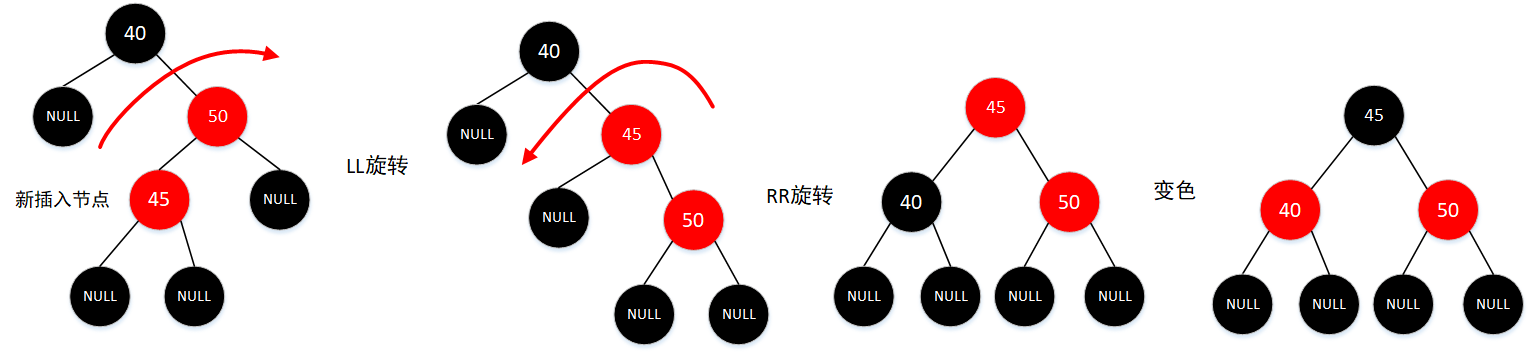
插入节点的父结点是红色,同时叔父节点是黑色,同时插入节点是其父节点的左子节点,而父节点是祖父节点的右子节点(RL),先进行一次LL旋转变成情况5,再进行一次RR旋转。变色情况同 4
整体构建过程
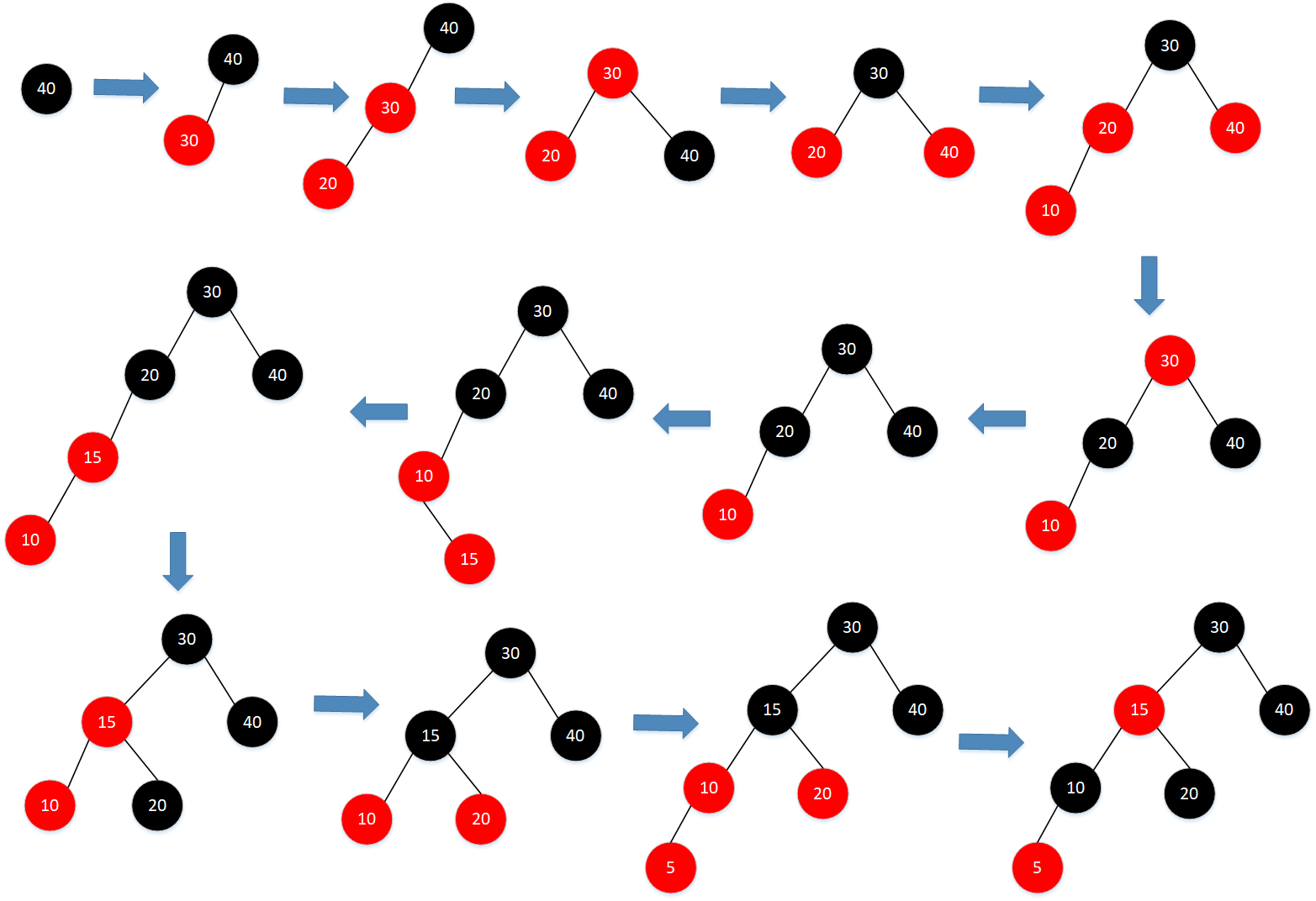
4.6.2 实现
1、创建节点类
public class RBTreeNode<T extends Comparable<T>> {
boolean color; // red or black
T key; // 键
RBTreeNode leftChildren; // 左子节点
RBTreeNode rightChildren; // 右子节点
RBTreeNode parent; // 父节点
public RBTreeNode(T key, boolean color) {
this.key = key;
this.color = color;
}
}
2、实现类(待改善)
public class RBTree<T extends Comparable<T>> {
private RBTreeNode<T> mRoot; // 根结点
private static final boolean RED = false;
private static final boolean BLACK = true;
public RBTree() {
mRoot=null;
}
private boolean isRed(RBTreeNode<T> node) {
return ((node!=null)&&(node.color==RED)) ? true : false;
}
private boolean isBlack(RBTreeNode<T> node) {
return !isRed(node);
}
// 前序遍历"红黑树"
private void preOrder(RBTreeNode<T> tree) {
if(tree != null) {
System.out.print(tree.key+"-" + tree.color + " ");
preOrder(tree.leftChildren);
preOrder(tree.rightChildren);
}
}
public void preOrder() {
preOrder(mRoot);
}
// 中序遍历"红黑树"
private void inOrder(RBTreeNode<T> tree) {
if(tree != null) {
inOrder(tree.leftChildren);
System.out.print(tree.key+" ");
inOrder(tree.rightChildren);
}
}
public void inOrder() {
inOrder(mRoot);
}
// 后序遍历"红黑树"
private void postOrder(RBTreeNode<T> tree) {
if(tree != null)
{
postOrder(tree.leftChildren);
postOrder(tree.rightChildren);
System.out.print(tree.key+" ");
}
}
public void postOrder() {
postOrder(mRoot);
}
// (递归实现)查找"红黑树x"中键值为key的节点
private RBTreeNode<T> search(RBTreeNode<T> x, T key) {
if (x==null)
return x;
int cmp = key.compareTo(x.key);
if (cmp < 0)
return search(x.leftChildren, key);
else if (cmp > 0)
return search(x.rightChildren, key);
else
return x;
}
public RBTreeNode<T> search(T key) {
return search(mRoot, key);
}
// (非递归实现)查找"红黑树x"中键值为key的节点
private RBTreeNode<T> iterativeSearch(RBTreeNode<T> x, T key) {
while (x!=null) {
int cmp = key.compareTo(x.key);
if (cmp < 0)
x = x.leftChildren;
else if (cmp > 0)
x = x.rightChildren;
else
return x;
}
return x;
}
public RBTreeNode<T> iterativeSearch(T key) {
return iterativeSearch(mRoot, key);
}
// 查找最小结点:返回tree为根结点的红黑树的最小结点。
private RBTreeNode<T> minimum(RBTreeNode<T> tree) {
if (tree == null)
return null;
while(tree.leftChildren != null)
tree = tree.leftChildren;
return tree;
}
public T minimum() {
RBTreeNode<T> p = minimum(mRoot);
if (p != null)
return p.key;
return null;
}
// 查找最大结点:返回tree为根结点的红黑树的最大结点。
private RBTreeNode<T> maximum(RBTreeNode<T> tree) {
if (tree == null)
return null;
while(tree.rightChildren != null)
tree = tree.rightChildren;
return tree;
}
public T maximum() {
RBTreeNode<T> p = maximum(mRoot);
if (p != null)
return p.key;
return null;
}
// 找结点(x)的后继结点。即,查找"红黑树中数据值大于该结点"的"最小结点"。
public RBTreeNode<T> successor(RBTreeNode<T> x) {
// 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
if (x.rightChildren != null)
return minimum(x.rightChildren);
// 如果x没有右孩子。则x有以下两种可能:
// (01) x是"一个左孩子",则"x的后继结点"为 "它的父结点"。
// (02) x是"一个右孩子",则查找"x的最低的父结点,并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。
RBTreeNode<T> y = x.parent;
while ((y!=null) && (x==y.rightChildren)) {
x = y;
y = y.parent;
}
return y;
}
// 找结点(x)的前驱结点。即,查找"红黑树中数据值小于该结点"的"最大结点"。
public RBTreeNode<T> predecessor(RBTreeNode<T> x) {
// 如果x存在左孩子,则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
if (x.leftChildren != null)
return maximum(x.leftChildren);
// 如果x没有左孩子。则x有以下两种可能:
// (01) x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。
// (01) x是"一个左孩子",则查找"x的最低的父结点,并且该父结点要具有右孩子",找到的这个"最低的父结点"就是"x的前驱结点"。
RBTreeNode<T> y = x.parent;
while ((y!=null) && (x==y.leftChildren)) {
x = y;
y = y.parent;
}
return y;
}
/*
* 对红黑树的节点(x)进行左旋转
*
* 左旋示意图(对节点x进行左旋):
* px px
* / /
* x y
* / \ --(左旋)-. / \ #
* lx y x ry
* / \ / \
* ly ry lx ly
*
*
*/
private void leftRotate(RBTreeNode<T> rbTreeNode) {
// 将当前节点的右子节点设为新节点
RBTreeNode<T> newRoot = rbTreeNode.rightChildren;
// 将新节点的左子节点设为当前节点的右子节点
rbTreeNode.rightChildren = newRoot.leftChildren;
// 将 “x的父亲” 设为 “y的父亲”
newRoot.parent = rbTreeNode.parent;
if (rbTreeNode.parent == null) {
this.mRoot = newRoot; // 如果 “x的父亲” 是空节点,则将y设为根节点
} else {
if (rbTreeNode.parent.leftChildren == rbTreeNode)
rbTreeNode.parent.leftChildren = newRoot; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
else
rbTreeNode.parent.rightChildren = newRoot; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
}
// 将 “x” 设为 “y的左孩子”
newRoot.leftChildren = rbTreeNode;
}
/*
* 对红黑树的节点(y)进行右旋转
*
* 右旋示意图(对节点y进行左旋):
* py py
* / /
* y x
* / \ --(右旋)-. / \ #
* x ry lx y
* / \ / \ #
* lx rx rx ry
*
*/
private void rightChildrenRotate(RBTreeNode<T> y) {
// 设置x是当前节点的左孩子。
RBTreeNode<T> x = y.leftChildren;
// 将 “x的右孩子” 设为 “y的左孩子”;
// 如果"x的右孩子"不为空的话,将 “y” 设为 “x的右孩子的父亲”
y.leftChildren = x.rightChildren;
if (x.rightChildren != null)
x.rightChildren.parent = y;
// 将 “y的父亲” 设为 “x的父亲”
x.parent = y.parent;
if (y.parent == null) {
this.mRoot = x; // 如果 “y的父亲” 是空节点,则将x设为根节点
} else {
if (y == y.parent.rightChildren)
y.parent.rightChildren = x; // 如果 y是它父节点的右孩子,则将x设为“y的父节点的右孩子”
else
y.parent.leftChildren = x; // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
}
// 将 “y” 设为 “x的右孩子”
x.rightChildren = y;
// 将 “y的父节点” 设为 “x”
y.parent = x;
}
// 插入节点
public void insert(T key) {
insert(new RBTreeNode<T>(key, BLACK));
}
// 插入节点后,修正红黑树
private void insert(RBTreeNode<T> node) {
int cmp;
RBTreeNode<T> y = null;
RBTreeNode<T> x = this.mRoot;
// 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。
while (x != null) {
y = x;
cmp = node.key.compareTo(x.key); //当前key h和插入的key进行比较
if (cmp < 0)
x = x.leftChildren;
else
x = x.rightChildren;
}
node.parent = y;
if (y!=null) {
cmp = node.key.compareTo(y.key); //判断插入到左边还是右边
if (cmp < 0)
y.leftChildren = node;
else
y.rightChildren = node;
} else {
this.mRoot = node;
}
// 2. 设置节点的颜色为红色
node.color = RED;
// 3. 将它重新修正为一颗二叉查找树
insertFixUp(node);
}
/*
* 红黑树插入修正函数
*
* 在向红黑树中插入节点之后(失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*1.Z是根节点(即Z插入前是一颗空树)
* 2.Z的叔节点是红色的
* 3.Z的叔节点是黑色的,并且局部呈现三角行(左右三角)
* 3.Z的叔节点是黑色的,并且局部呈现直线角行(左右直线)
*
* 参数说明:
* node 插入的结点
*
*/
private void insertFixUp(RBTreeNode<T> addNode) {
RBTreeNode<T> parent, gparent;
// 若“父节点存在,并且父节点的颜色是红色”
while (((parent = addNode.parent)!=null) && isRed(parent)) {
gparent = parent.parent;
//若“父节点”是“祖父节点的左孩子”
if (parent == gparent.leftChildren) {
// Case 1条件:叔叔节点是红色
RBTreeNode<T> uncle = gparent.rightChildren;
if ((uncle!=null) && isRed(uncle)) {
uncle.color = BLACK;
parent.color = BLACK;
gparent.color = RED;
addNode = gparent;
continue;
}
// Case 2条件:叔叔是黑色,且当前节点是右孩子
if (parent.rightChildren == addNode) {
RBTreeNode<T> tmp;
leftRotate(parent);
tmp = parent;
parent = addNode;
addNode = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是左孩子。
parent.color = BLACK;
gparent.color = RED;
rightChildrenRotate(gparent);
} else { //若“z的父节点”是“z的祖父节点的右孩子”
// Case 1条件:叔叔节点是红色
RBTreeNode<T> uncle = gparent.leftChildren;
if ((uncle!=null) && isRed(uncle)) {
uncle.color = BLACK;
parent.color = BLACK;
gparent.color = RED;
addNode = gparent;
continue;
}
// Case 2条件:叔叔是黑色,且当前节点是左孩子
if (parent.leftChildren == addNode) {
RBTreeNode<T> tmp;
rightChildrenRotate(parent);
tmp = parent;
parent = addNode;
addNode = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是右孩子。
parent.color = BLACK;
gparent.color = RED;
leftRotate(gparent);
}
}
// 将根节点设为黑色
mRoot.color = BLACK;
}
/*
* 红黑树删除修正函数
*
* 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
*
*
* 参数说明:
* node 待修正的节点
*/
private void removeFixUp(RBTreeNode<T> fixNode, RBTreeNode<T> parent) {
RBTreeNode<T> other;
while ((fixNode==null || isBlack(fixNode)) && (fixNode != this.mRoot)) {
if (parent.leftChildren == fixNode) {//删除的节点是左节点
other = parent.rightChildren;
if (isRed(other)) {
// Case 1: x的兄弟w是红色的
other.color = BLACK;
parent.color = RED;
leftRotate(parent);
other = parent.rightChildren;
}
if ((other.leftChildren==null || isBlack(other.leftChildren)) &&
(other.rightChildren==null || isBlack(other.rightChildren))) {
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
other.color = RED;
fixNode = parent;
parent = fixNode.parent;
} else {
if (other.rightChildren==null || isBlack(other.rightChildren)) {
// Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
other.leftChildren.color = BLACK;
other.color = RED;
rightChildrenRotate(other);
other = parent.rightChildren;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
other.color = parent.color;
parent.color = BLACK;
other.rightChildren.color = BLACK;
leftRotate(parent);
fixNode = this.mRoot;
break;
}
} else { //删除的节点是右节点
other = parent.leftChildren;
if (isRed(other)) {
// Case 1: x的兄弟w是红色的
other.color = BLACK;
parent.color = RED;
rightChildrenRotate(parent);
other = parent.leftChildren;
}
if ((other.leftChildren==null || isBlack(other.leftChildren)) &&
(other.rightChildren==null || isBlack(other.rightChildren))) {
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
other.color = RED;
fixNode = parent;
parent = fixNode.parent;
} else {
if (other.leftChildren==null || isBlack(other.leftChildren)) {
// Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
other.rightChildren.color = BLACK;
other.color = RED;
leftRotate(other);
other = parent.leftChildren;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
other.color = parent.color;
parent.color = BLACK;
other.leftChildren.color = BLACK;
rightChildrenRotate(parent);
fixNode = this.mRoot;
break;
}
}
}
if (fixNode!=null)
fixNode.color = BLACK;
}
// 删除结点(delNode),并返回被删除的结点
private void remove(RBTreeNode<T> delNode) {
RBTreeNode<T> child, parent;
boolean color;
// 被删除节点的"左右孩子都不为空"的情况。
if ( (delNode.leftChildren!=null) && (delNode.rightChildren!=null) ) {
// 被删节点的后继节点。(称为"取代节点")
// 用它来取代"被删节点"的位置,然后再将"被删节点"去掉。
RBTreeNode<T> replace = delNode;
// 获取后继节点
replace = replace.rightChildren;
while (replace.leftChildren != null)
replace = replace.leftChildren;
// "node节点"不是根节点(只有根节点不存在父节点)
if (delNode.parent!=null) {
if (delNode.parent.leftChildren == delNode)
delNode.parent.leftChildren = replace;
else
delNode.parent.rightChildren = replace;
} else {
// "node节点"是根节点,更新根节点。
this.mRoot = replace;
}
// child是"取代节点"的右孩子,也是需要"调整的节点"。
// "取代节点"肯定不存在左孩子!因为它是一个后继节点。
child = replace.rightChildren;
parent = replace.parent;
// 保存"取代节点"的颜色
color = replace.color;
// "被删除节点"是"它的后继节点的父节点"
if (parent == delNode) {
parent = replace;
} else {
// child不为空
if (child!=null)
child.parent = parent;
parent.leftChildren = child;
replace.rightChildren = delNode.rightChildren;
delNode.rightChildren.parent = replace;
}
replace.parent = delNode.parent;
replace.color = delNode.color;
replace.leftChildren = delNode.leftChildren;
delNode.leftChildren.parent = replace;
if (color == BLACK) //红色直接删除 黑色删除后维护
removeFixUp(child, parent);
delNode = null;
return ;
}
if (delNode.leftChildren !=null) {
child = delNode.leftChildren;
} else {
child = delNode.rightChildren;
}
parent = delNode.parent;
// 保存"取代节点"的颜色
color = delNode.color;
if (child!=null)
child.parent = parent;
// "node节点"不是根节点
if (parent!=null) {
if (parent.leftChildren == delNode)
parent.leftChildren = child;
else
parent.rightChildren = child;
} else {
this.mRoot = child;
}
if (color == BLACK)
removeFixUp(child, parent);
delNode = null;
}
/*
* 删除结点(z),并返回被删除的结点
*
* 参数说明:
* tree 红黑树的根结点
* z 删除的结点
*/
public void remove(T key) {
RBTreeNode<T> node;
if ((node = search(mRoot, key)) != null)
remove(node);
}
/*
* 销毁红黑树
*/
private void destroy(RBTreeNode<T> tree) {
if (tree==null)
return ;
if (tree.leftChildren != null)
destroy(tree.leftChildren);
if (tree.rightChildren != null)
destroy(tree.rightChildren);
tree=null;
}
public void clear() {
destroy(mRoot);
mRoot = null;
}
/*
* 打印"红黑树"
*
* key -- 节点的键值
* direction -- 0,表示该节点是根节点;
* -1,表示该节点是它的父结点的左孩子;
* 1,表示该节点是它的父结点的右孩子。
*/
private void print(RBTreeNode<T> tree, T key, int direction) {
if(tree != null) {
if(direction==0) // tree是根节点
System.out.printf("%2d(B) is root\n", tree.key);
else // tree是分支节点
System.out.printf("%2d(%s) is %2d's %6s child\n", tree.key, isRed(tree)?"R":"B", key, direction==1?"rightChildren" : "leftChildren");
print(tree.leftChildren, tree.key, -1);
print(tree.rightChildren,tree.key, 1);
}
}
public void print() {
if (mRoot != null)
print(mRoot, mRoot.key, 0);
}
}
3、测试类
public class RBTreeNode<T extends Comparable<T>> {
boolean color; // red or black
T key; // 键
RBTreeNode leftChildren; // 左子节点
RBTreeNode rightChildren; // 右子节点
RBTreeNode parent; // 父节点
public RBTreeNode(T key, boolean color) {
this.key = key;
this.color = color;
}
}