树状数组————(神奇的区间操作)蒟蒻都可以看懂,因为博主就是个蒟蒻
树状数组
F三、蒟蒻看法
树状数组是十分神奇的算法(至少我这么认为,我至今都好奇,第一个人是如何想出来的,oi深似海比海深比海深)。
F二、树状数组存在的含义(要它干啥子)用途!用途!
其实标题已经说明了,它可以支持一些区间操作,比如最基础的单点修改、区间查询,区间修改,单点查询,和一些精巧的应用。(哦~~,我的数组也可以实现)那你就等着T吧。树状数组的速度是真的快,比线段树都要快!但是理解起来有一点点麻烦,所以有了这篇博客。
F一、什么是树状数组
与它的名字一样,就是用数组来实现树形结构,是不是很腻害!而且代码短!代码短!

一、初识树状数组(介绍)

对,他就是这样的,红色的代表我们今天要学的树状数组,而黑色便是普通的数组,这张图代表了他们的对应关系。(??what?What are you say?)
不要急,咱们先来点基础知识。
二、前置知识(lowbit可是树状数组的灵魂)
我们都知道,任何一个数都可以用2不同的幂相加得到:
x=2i1+2i2+2i3+2i4+……+2i+n,其中i1>i2>i3>i4>……>im,例如:7=22+21+20=4+2+1.
这也就意味着一段区间可以划分为大小不同的段数,例如:[1,7]=[1,4]+[5,6]+[7,7].(上面的例子数的大小与这个例子的区间长度一一对应)。
上面的图不好,咱们再来一张。(不慌不慌)

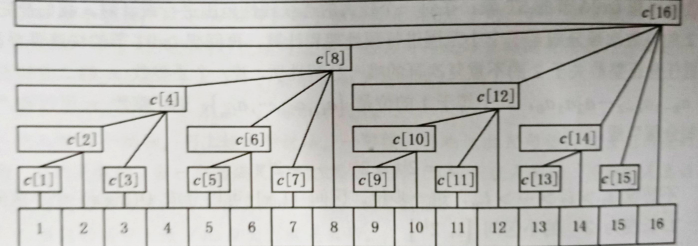
同样,最底下为输入的数(也就是数组,这里设为a[i]),上方对印的便是树状数组。
咱们还拿7为例子,[1,7]=[1,4]+[5,6]+[7,7]同等与a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]=c[4]+c[6]+c[7].
但这是如何实现的呢?答:lowbit(n).
又要前置知识了,lowbit可以求出一个数在二进制数中最低位1以其他后边的0所构成的值。理解的人请跳过本段。首先是二进制数,二进制讲解:咱们平时的运算都是十进制的(即逢十进一),二进制便是逢二进一。为了实现lowbit(n)操作,我们将n取反变为~n(取反就是,将原本为1的变为0,为0的变为1),这样原本n的最后一位1的位置(设为k)~n的第k位为0,因为原本n的最后一位1的位置为k,所以k以后全是0,所有~n第k位以后全是1,此时我们将~n+1(此时,~n第k位以后的1都会因为进位变成0,而第k位因为进位变成了1),这时,n与~n只有第k位都是1(即n的最低位的1),其他位置数都不相等,再用n&(~n+1)(&如果此位置都是1,返回1,否则返回0),所以返回了n最低位1以其他后边的0所构成的值。在补码(取反加以)的表示下,~n=-1-n,所以:n=~n+1,因此:lowbit(n)=n&(~n+1)=n&(-n). 好,lowbit()讲解结束,别看难证明,计算机里此种运算飞快(因为计算机本身就是二进制的)。
(so~ lowbit与树状数组有what关系)

三、区间查询
再看上面的图,找找关系。(哇!没找见)很好,举个例子,还是7,咱们把7取lowbit,lowbit(7)=1,lowbit(7-1)=2,lowbit(7-1-2)=4,有没有什么发现,没错,它一直取lowbit可以得到它每段的长度(没个啥子用呀),再看,7,7-1=6,7-1-2=4,c[7]+c[6]+c[4]=结果。(这回总算有用了)
上代码!
查询前缀和(没错,你已经掌握了树状数组支持的基本操作之一————查询前缀和)
inline int ask(int x) {//x的前缀和 int ans=0; for(; x; x -= x & -x) ans+=c[x]; return ans; }
那为啥要查询前缀和呢?照常举例子,比如咱们要查询[l,r]中所有数的和,咱们只需要计算ask(r)-ask(l-1)。
四、单点修改
树状数组支持的第二个操作是单点修改(此处运用单点增加,变化不大)。
咱们再看看lowbit与上面的图,很好,你还是看不出来,举个例子,还是7,咱们把7取lowbit,lowbit(7)=1,lowbit(7+1)=8,lowbit(7+1+2)=16,再看,7,7+1=8,7+1+8=16,c[16]包括c[8],c[8]包括c[7]。
当咱们修改了a[x](假设将a[x]加上b),咱们同时也要将它的祖先(包含它的c[])全部修改,这样才能支持查询前缀和的操作。
上代码!
单点增加
inline void add(int x,int b) {//将序列中一个数a[x]及其祖先加上b; for(; x<=n; x += x & -x) c[x]+=b; }
没错你学会了,树状数组!

值得注意的是,当你输入原数组时记得也要执行add(x,a[x]).
for(int i=1;i<=n;i++) { cin>>a[i]; add(i,a[i]); }
五、支持单点修改、区间查询的树状数组全貌
来!欣赏(姑且瞎看)一下代码的全貌吧!
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int n,m; int a[500008],c[500008]; inline void add(int x,int b) { for(; x<=n; x += x & -x) c[x]+=b; } inline int ask(int x) { int ans=0; for(; x; x -= x & -x) ans+=c[x]; return ans; } int main() { cin>>n>>m; for(int i=1;i<=n;i++) { cin>>a[i]; add(i,a[i]); } while(m--) { int p,x,k; cin>>p>>x>>k; if(p==1) add(x,k); else cout<<ask(k)-ask(x-1)<<endl; } }
六、支持区间修改、单点查询的树状数组
先来区间修改,不知你是否有听过差分。差分是一种很常见又很神奇的算法,它可以通过改变两个点的值,使整段区间发生修改。
差分讲解:假设a[]为原数组,b[]为差分数组
则:b[i]=a[i]-a[i-1]
b[1]=a[1]-a[0] b[2]=a[2]-a[1] b[3]=a[3]-a[2] …… b[n]=a[n]-a[n-1]
若将a[i]到a[j](i<j)同时加x,则b[i]以前并未发生改变,b[i]=b[i]+x,b[i+1]到b[j](包括b[i+1]和b[j])之间并未发生改变,b[j+1]=b[j+1]-x.
举个例子,将a[3]到a[7]同时加上x,因为b[3]以前的数字并不由a[3]到a[7]之间的数字得到,由于a[3]=a[3]+x,而a[2]=a[2],所以b[3](现在的)=(a[3]+x)-a[2]=a[3]-a[2]+x,b[3](原来的)=a[3]-a[2],所以b[3](现在的)=b[3](原来的)+x.因为a[3]到a[7]所有数字都加上了x所以b[4]到b[7]之间的数并没有发生变化,例子:b[4](现在的)=(a[4]+x)-(a[3]+x)=a[4]-a[3],b[4](原来的)=a[4]-a[3],所以b[4](现在的)=b[4](原来的).可是到了b[8]的时候,a[7]=a[7]+x,而a[8]=a[8],所以b[8](现在的)=a[8]-(a[7]+x)=a[8]-a[7]-x,b[8](原来的)=a[8]-a[7],b[8](现在的)=b[8](原来的)-x.证毕。
这样我们就可以通过改变a[i]和a[j+1]的大小,将a[i]到a[j]全部改变了。
add函数并未发生变化
add函数
inline void add(int x,int y) { for(;x<=n;x+=(x&-x)) c[x]+=y; }
主函数有一些改变
add(a,c);add(b+1,-c);
通过改变两个点来改变整段添加操作。
(有啥子用?搞一堆乱七八糟的。)
再来单点查询。
它是很有用的,差分还有一个性质:差分与前缀和(前面所有数字相加的和)互逆。意思就是数组差分后求个前缀和等于原数组。
是不是恍然顿悟!(查询a[k],就查询a[k]差分完后的前缀和)
没错,之前(支持单点修改、区间查询的树状数组)的查询方式就是查前缀和,所以查询代码还不用修改,甚至主程序里相关内容更简单了。
ask函数
inline int ask(int x) { int ans=0; for(;x;x-=(x&-x)) ans+=c[x]; return ans; }
主程序
cout<<ask(x)<<endl;
七、支持区间修改、单点查询的树状数组代码全貌
注意在输入原数组时记得也要用差分
for(int i=1;i<=n;i++) { scanf("%d",&a[i]); add(i,a[i]-a[i-1]);
}
好了上全部代码!

#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int n,m; int a[500008],c[500008]; inline void add(int x,int y) { for(;x<=n;x+=(x&-x)) c[x]+=y; } inline int ask(int x) { int ans=0; for(;x;x-=(x&-x)) ans+=c[x]; return ans; } int main() { cin>>n>>m; for(int i=1;i<=n;i++) { scanf("%d",&a[i]); add(i,a[i]-a[i-1]); } for(int i=1;i<=m;i++) { int p; cin>>p; if(p==1) { int a,b,c; cin>>a>>b>>c; add(a,c);add(b+1,-c); } else { int x; cin>>x; cout<<ask(x)<<endl; } } }
(一堆骚操作,乱七八糟,跟直接用数组解决有区别吗?)
显然是有的。
七、复杂度正儿八经瞎七八证明
首先是支持单点修改、区间查询的树状数组,虽然修改的速度变慢了,从O(1)变成了O(log(n)),但它为查询操作提供了方便,使查询从O(n)变成了O(log(n)).
其次是支持区间修改、单点查询的树状数组,虽然查询的速度变慢了,从O(1)变成了O(log(n)),但它为修改操作提供了方便,使查询从O(n)变成了O(log(n)).
(没看出我是复制的吧!qwq)
八、树状数组解决逆序对
很好,在博主奋力的解说下(可能压根没人看到这里吧),和严谨的复杂度证明后,相信你已经对树状数组的基操有了很深的认识。
一起看一道,树状数组模版题吧!

输入样例:
6
5 4 2 6 3 1
输出样例:
11
是不是有些许蒙蔽。

我先说明一下逆序对:逆序对就是如果i > j && a[i] < a[j],这两个就算一对逆序对,简单来说,所有逆序对的个数和就是找每一个数的前面有几个比他的大的数,他们加起来的和就是逆序对的总数
(这也能用树状数组?)

事实证明是可以的。
我要开始讲解了!(先自我思考一下!)

首先,我们将数b[i]输入,然后每次都把c[b[i]]++,查询c[b[i]]的后缀和(顾名思义,就是后面全部数字的和,但此处的后缀和不包括自己),此处的后缀和代表的就是在b[i]之前输入但大于b[i]的数(即:符合i > j && a[i] < a[j])个数之和,也就是逆序对的个数。
例子来惹!
第一次把5的位置加1,它的后缀和(以下全为不包括自己的后缀和)为0,sum+=0(sum记录逆序对个数)
![]()
![]()
![]()
第二次把4的位置加1,它的后缀和为1,sum+=1
![]()
![]()
![]()
第三次把2的位置加1,它的后缀和为2,sum+=2
![]()
![]()
![]()
第四次把6的位置加1,它的后缀和为0,sum+=0
![]()
![]()
![]()
第五次把3的位置加1,它的后缀和为3,sum+=3
![]()
![]()
![]()
第五次把1的位置加1,它的后缀和为5,sum+=5
![]()
![]()
![]()
此时sum=11,输出sum。
(哇!明显炸了呀!序列数字不超过109呀,怎么存?)
没错!没错!而且很明显还没用到树状数组。那它到底如何实现的呢?
首先要离散化(有链接)!(因为需要用到桶的思想)
虽然每个数的值很大,但是(n<=5*105)却是可以开下的,离散化可以保证数字间的相对大小不变,而本题恰恰只需要这点。
代码!代码!
for(int i=1;i<=n;i++) { scanf("%d",&a[i]); A[i]=a[i]; } sort(a+1,a+n+1); int size=unique(a+1,a+n+1)-a; for(int i=1;i<=n;i++) { b[i]=lower_bound(a+1,a+size+1,A[i])-a; }
实现了把a[](输入的数组),离散化成b[]。
接下来就是如何和树状数组联系了。
通过上述讲解,我们将问题简化为了,每次在c[b[i]]++,查询后缀和。(这不是树状数组所支持的单点修改,区间查询吗?)
先看单点修改。
同上文一样在b[i]的位置上加上1。
for(int i=1;i<=n;i++) { add(b[i],1);//添加操作 //sum+=i-ask(b[i]);//查询操作 }
(但是后缀和怎么办?我们求的是前缀和呀?)
i-前缀和=不包括自己的后缀和(因为i代表这是第几个数,而前缀和是1~i(因为每回只加1))
所以就解决了!
for(int i=1;i<=n;i++) { add(b[i],1); sum+=i-ask(b[i]); }
此题解将输入的数存在a[],将离散化的数存在b[](就是之前树状数组模版中的普通数组),树状数组用c[]。
代码全貌!
//用树状数组实现查询逆序对个数 #include<iostream> #include<algorithm> #include<cstdio> #include<cstring> using namespace std; int n,a[500005],A[500005],b[500005],c[500005]; long long sum; inline void add(int x,int b) { for(; x<=n; x += x & -x) c[x]+=b; } inline int ask(int x) { int ans=0; for(; x; x -= x & -x) ans+=c[x]; return ans; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); A[i]=a[i]; } sort(a+1,a+n+1); int size=unique(a+1,a+n+1)-a; for(int i=1;i<=n;i++) { b[i]=lower_bound(a+1,a+size+1,A[i])-a; } for(int i=1;i<=n;i++) { add(b[i],1); sum+=i-ask(b[i]); } printf("%lld",sum); }
记得开龙龙(long long)啊!不开龙龙见祖宗!
没开龙龙

开了龙龙
博主语录:
1、树状数组是真的神奇!不明白怎么想出来的。
2、树状数组虽然比较难理解,但是速度,和代码难度是真的优秀!建议勤加练习。
3、若是没能理解可以先看看线段树,几乎oi界的人都是先理解了线段树的。(可能是我太菜,目光短浅)


