常用的数据结构
1.数组(Array)
数组可以说是最基本的数据结构。它是将相同类型的一些数据有序的集合在一起。
一个数组可以包含多个同类型的数据元素。
可以按照数据类型分为整型数组、字符型数组、浮点型数组、对象数组等。
可以按照维度分为一维数组、二维数组、多维数组等。
- 2.队列(Queue)
队列也是一种特殊的线性表。只允许在一端(队尾)进行插入,在另一端(队头)进行删除。
线性表就是各个数据元素之间具有线性关系。就像一条线一样。有头有尾,中间一个结点连着一个结点,不可间断。
队列就像水管一样,水只能从一端流入,从另一端流出。 - 3.链表(Linked List)
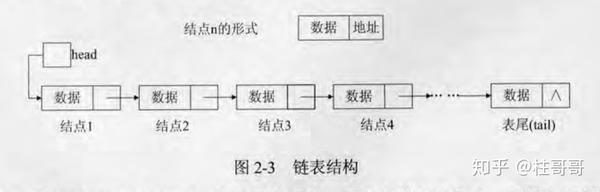
链表的元素是按照链式存储的。也是线性结构中的一种。线性结构包括顺序结构和链表结构两种。
这种存储在物理上并非连续的,而是每个元素包括两个部分,一部分是自己的数据,另一部分是引用域,指向下一个元素所在的地址。
链表的逻辑关系是通过引用域串联起来的。
线性结构中的顺序表结构在进行插入或者删除的时候,需要移动大量的数据。而链表结构最多只需要修改关联的前后两个结点的引用域即可。
链表包含单向链表和双向链表,单向链的引用域只指向下一个元素的地址,双向链表的引用域既包含指向下一个的地址,也有指向上一个的地址。 - 4.树(Tree)
典型的非线性结构,有且仅有一个根结点,根结点会有一个或多个子结点。
然后子结点也可能会有一个或多个子结点。但是,每个子结点都只会有一个父结点。
终结点没有子结点。
每个节点后面的所有节点组成的树称为这个结点的子树。
二叉树是一种比较特殊的树,每一个结点最多都只有两个子结点。称为左结点和右结点。
二叉树又包括完全二叉树(有子结点的结点都有两个子结点),和非完全二叉树(有些结点只有一个子结点)。 - 5.堆(Heap)
堆是一种特殊的树形结构,我们一般讨论的堆都是二叉堆。
堆的特点是根结点的值是所有结点中最小的或者最大的。并且根结点的子树也是一个堆结构。 - 6.栈(Stack)
栈是一种特殊的线性表,只能在表的一端(栈顶)进行插入(入栈)和删除(出栈)操作。
第一个插入的数据会被后面插入的不断的压入栈底。要想操作栈底的数据,只能先将其推到栈顶。 - 7.图(Graph)
图是另外一种非线性结构,例如通信网络、交通网络、人机关系网络,都可以归为图结构
图可以分为无向图和有向图,
无向图没有方向,从A到B和从B到A一样,
有向图具有方向,就像单行道,只能从A到B,不可以逆向从B到A
连接图的某个定点到其他所有定点的边的数量称为该顶点的度。 - 8.散列表(Hash)
源自散列函数(Hash function),其思想是如果在结构中存在关键字和T相等的记录,那么必定在F(T)的存储位置可以找到该记录,这样就可以不用进行比较而直接取得所查记录
2.链表结构
/**
* 定义数据结构中的元素
*/
static class DataElement {
String key;
String other_messages;
public DataElement(String key, String other_messages) {
this.key = key;
this.other_messages = other_messages;
}
}
/**
* 定义链表结构
* 链表包含单向链表和双向链表,单向链的引用域只指向下一个元素的地址,双向链表的引用域既有指向下一个的,也有指向上一个的
*/
static class DataLinkedList {
DataElement dataElement;
DataLinkedList nextNode;
//我们这里只做查找算法的示例,省去添加节点,删除节点等其他方法,只做查找
/**
* 在链表的尾部追加数据
*
* @param head 链表的表头
* @param data 要添加的数据
* @return 添加后的链表元素(数据+引用域)
*/
static DataLinkedList addData(DataLinkedList head, DataElement data) {
DataLinkedList node = new DataLinkedList();//新追加的结点是在结尾追加
node.dataElement = data;//保存数据
node.nextNode = null;//表尾引用域为null,
DataLinkedList element = head;
if (element == null) {//链表的表头为null,是个空链表,直接将head指向新节点
head = node;
return head;
}
while (element.nextNode != null) {//找到链表的尾部,如果已知链表尾部,则可以直接用,不用再从表头查找
element = element.nextNode;
}
element.nextNode = node;//将链表的尾部指向新追加的结点
return node;
}
/**
* 在表头追加数据
*
* @param head 表头
* @param data 要添加的数据
* @return 添加后的链表元素(数据+引用域)
*/
static DataLinkedList addHeadData(DataLinkedList head, DataElement data) {
DataLinkedList node = new DataLinkedList();//新追加的结点是在链表头部追加
node.dataElement = data;//保存数据
node.nextNode = head;//指向下一个元素是之前的表头
head = node;//表头变成新增的这个元素
return head;
}
/**
* 在指定的key后面追加数据
*
* @param head 表头
* @param key 元素数据的key
* @param data 要插入的新数据
* @return 插入的新元素(数据+引用)
*/
static DataLinkedList insertData(DataLinkedList head, String key, DataElement data) {
DataLinkedList keyData = null;
//查找key所在的位置
DataLinkedList temp = head;
while (temp != null) {
DataElement date 


