机器人运动学（二）-欧拉角

书接上文，本篇文章主要介绍欧拉角
学习参考资料
# 旋转变换（二）欧拉角
# 「 SLAM lesson-3.4 」欧拉角度定义、应用、缺点
# 欧拉角细节/旋转顺序/内旋外旋

欧拉角

欧拉角来自欧拉旋转定理

在三维空间里，假设一个刚体在做一个旋转的时候，刚体内部至少有一点固定不动，则此位移等价于一个绕着包含那固定点的固定轴的旋转。

换句话讲，三维空间中任意旋转都可以用绕某点旋转的三个角度来表示

然而想要规范地使用欧拉角，还需要搞清楚以下几个问题：

1.三个旋转角的组合方式
2.参照的坐标轴
3.三个旋转角如何记

1.旋转角的组合

欧拉角一般具有两大类表示方式，按照旋转次序又分为6小类

Proper Euler angles（z-x-z，x-y-x，y-z-y，z-y-z，x-z-x，y-x-y）
Tait-Bryan angles（x-y-z，y-z-x，z-x-y，x-z-y，z-y-x，y-x-z）

一般使用Tait-Bryan angles

2.内旋/外旋

现假设世界坐标系XYZ中存在一个物体，物体相对自己的坐标系xyz，初始状态下，XYZ与xyz重合，当物体旋转的同时，相对物体的坐标系xyz也随之旋转。

因此有内旋外旋的区别： 外旋按照坐标系XYZ旋转，内旋按照坐标系xyz旋转。

3.三个旋转角的记法

顺序	飞行器	望远镜	符号	角速度
第一	heading	azimuth	\(\theta\)	yaw
第二	attitude	elevation	\(\phi\)	pitch
第三	bank	tilt	\(\psi\)	roll

如图

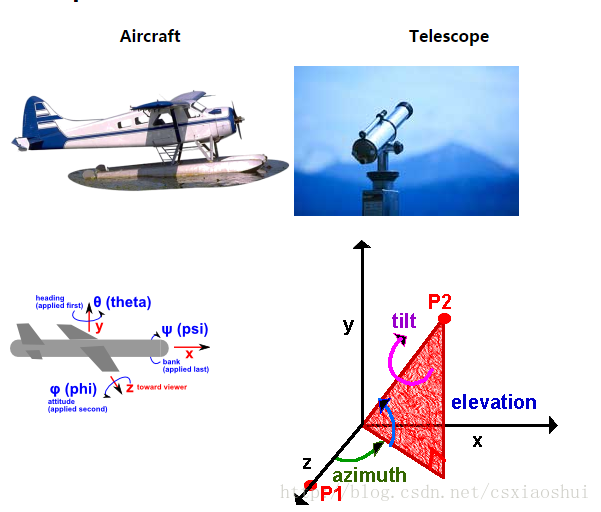
在欧拉角中，较常用“偏航-俯仰-滚转”(yaw-pitch-roll)三个角度来描述一个旋转

在解决了这三个问题后，描述一个能表示确定姿态/旋转的欧拉角，形式应类似下述例子：

旋转角度(\(\alpha,\beta,\gamma)\)，旋转顺序(z->y->x)，外旋

4.欧拉角的缺点-连续与万向锁问题(Gimbal lock)

对于 连续的旋转 ，这边要指出：
如果有两组旋转角\((\alpha_{1},\beta_{1},\gamma_{1})\)与\((\alpha_{2},\beta_{2},\gamma_{2})\)，并不能够用一组旋转角\((\alpha_{1}+\alpha_{2},\beta_{1}+\beta_{2},\gamma_{1}+\gamma_{2})\)来表示两次连续的旋转。

万向锁问题(Gimbal lock) 是欧拉角的一个重大缺点：在仰俯角为$\pm 90^{\circ} $的时候，两个旋转轴重合，系统会丢失一个旋转的自由度。
理论上可以证明，只要我们想用三个实数表达三维旋转的时候，就不可避免地碰到奇异性的问题。

这边从数学意义上去理解，顺带引出欧拉角的旋转矩阵表示

旋转角度(\(\alpha,\beta,\gamma)\)，旋转顺序(x->y->z)，内旋

很容易得到其旋转矩阵为\(R_{x}(\alpha)*R_{y}(\beta)*R_{z}(\gamma)\)

\[R=\begin{bmatrix} 1 & 0 & 0\\ 0 & \cos\alpha & -\sin\alpha \\ 0 & \sin\alpha & \cos\alpha \end{bmatrix}* \begin{bmatrix} \cos\beta & 0 & \sin\beta \\ 0 & 1 & 0 \\ -\sin\beta & 0 & \cos\beta \end{bmatrix}* \begin{bmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0\\ 0 & 0 & 1 \end{bmatrix} \]

当\(\beta=\frac{\pi}{2}\)的时候

\[R=\begin{bmatrix} 1 & 0 & 0\\ 0 & \cos\alpha & -\sin\alpha \\ 0 & \sin\alpha & \cos\alpha \end{bmatrix}* \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0 \end{bmatrix}* \begin{bmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0\\ 0 & 0 & 1 \end{bmatrix} \]

\[R=\begin{bmatrix} 0 & 0 & 1 \\ \sin\alpha & \cos\alpha & 0 \\ -\cos\alpha & \sin\alpha & 0 \end{bmatrix}* \begin{bmatrix} \cos\gamma & -\sin\gamma & 0 \\ \sin\gamma & \cos\gamma & 0\\ 0 & 0 & 1 \end{bmatrix}= \begin{bmatrix} 0 & 0 & 1 \\ \sin(\alpha+\gamma) & \cos(\alpha+\gamma) & 0 \\ -\cos(\alpha+\gamma) & \sin(\alpha+\gamma) & 0 \end{bmatrix} \]

可以看到，这个情况下，修改\(\alpha\)与修改\(\gamma\)效果是一样的，也就是出现了万向锁问题

这边顺带提一嘴：每种特定顺序的外旋等价于其相反顺序的内旋

既然欧拉角有如此问题，下一篇文章将学习另一种描述三维旋转的方式——四元数
欲知后事如何，且听下回分解!─=≡Σ(((つ•̀ω•́)つ