为什么你打不过我呢?——博弈论(一)
PS:本文尚未完结,正在努力填坑......争取这个寒假结束......
终究是我想太多(upd 2021.2.24)
序:
博弈是信息学和数学试题中常会出现的一种类型,算法灵活多变是其最大特点,而其中有一类试题更是完全无法用常见的博弈树来进行解答。 寻找必败态即为针对此类试题给出一种解题思路。
在此引用wiki上的表述:
博弈论 ,是经济学的一个分支,主要研究具有竞争或对抗性质的对象,在一定规则下产生的各种行为。博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
通俗地讲,博弈论主要研究的是:在一个游戏中,进行游戏的多位玩家的策略。
公平组合游戏
公平组合游戏的定义如下:
- 游戏有两个人参与,二者轮流做出决策,双方均知道游戏的完整信息;
- 任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关,而与游戏者无关;
- 游戏中的同一个状态不可能多次抵达,游戏以玩家无法行动为结束,且游戏一定会在有限步后以非平局结束。
大部分的棋类游戏都 不是 公平组合游戏,如国际象棋、中国象棋、围棋、五子棋等(因为大家都不是小孩子了)。
博弈的类型:合作博弈、非合作博弈、完全信息博弈、非完全信息博弈、静态博弈、动态博弈,等等。
基本博弈
理论:
Point 1 定义P-position和N-position:其中P代表Previous,N代表Next。
Note 1 直观的说,上一次move的人有必胜策略的局面是P-position,也就是“先手必败”,现在轮到move的人有必胜策略的局面是N-position,也就是“先手可保证必胜”。Point 1.1 无法进行任何移动的局面(也就是terminal position)是P-position;
Point 1.2 可以移动到P-position的局面是N-position;
Point 1.3 所有移动都导致N-position的局面是P-position。Point 2 P/N状态有如下性质:
Point 2.1 若面临末状态者为获胜则末状态为胜态否则末状态为必败态。
Point 2.2 一个局面是胜态的充要条件是该局面进行某种决策后会成为必败态。
Point 2. 3 一个局面是必败态的充要条件是该局面无论进行何种决策均会成为胜态Note 2 P点: 即必败点,某玩家位于此点,只要对方无失误,则必败;
Note 3 N点: 即必胜点,某玩家位于此点,只要自己无失误,则必胜。
个人理解:
决策:move的方式,而大部分较为简单题目中会给出choose的方式,但是,难题都是让你自己去想那个best choose
最优决策:竞争双方执行的move方式。
取石子游戏(NIM)
取石子游戏是一个古老的博弈游戏,发源于中国,它是组合数学领域的一个经典问题。它有许多不同的玩法,基本上是两个玩家,玩的形式是轮流抓石子,胜利的标准是抓走了最后的石子。
考虑代码如何进行:
step 1:将所有终结位置标记为必败点(P点);
step 2:将所有一步操作能进入必败点(P点)的位置标记为必胜点(N点)
step 3:如果从某个点开始的所有一步操作都只能进入必胜点(N点) ,则将该点标记为必败点(P点) ;
step 4:如果在步骤3未能找到新的必败(P点),则算法终止;否则,返回到步骤2
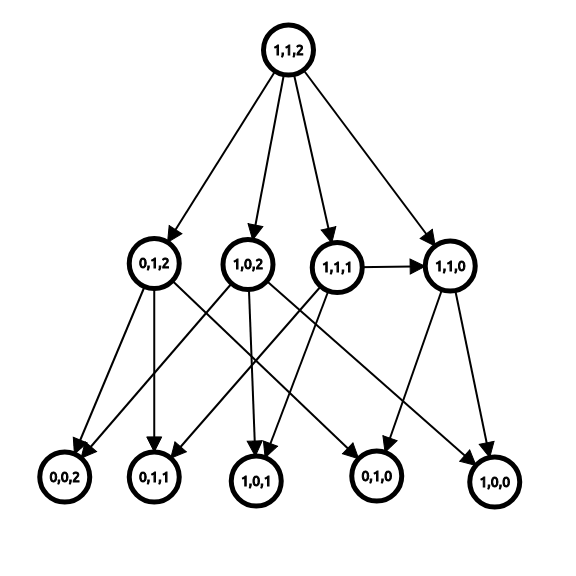
那么此时我们就有了博弈图(引用wiki):
节点(i,j,k)表示三堆石子分别为(i,j,k)时的状态。注意:途中没有标注P,N请自己手模一下,增加理解深度。(好吧就是因为我真的不想画图......)
Part 1 巴士博弈
问题模型:只有一堆n个物品,两个人轮流从这堆物品中取物,规定每次至少取一个,最多取m个,最后取光者得胜。
解决思路:
1 当n=m+1时,因为一次最多只能取m个,所以无论先取者拿走多少个,后取者都能够一次拿走剩余的物品,后者胜。
2 由1,当一方面对的局势是n%(m+1)=0时,其面临的是必败的局势。
3 由2,当n=(m+1)*r+s,(r为任意自然数,s≤m)时, 如果先取者要拿走s个物品,如果后取者拿走x(≤m)个,那么先取者再拿走m+1-k个,结果剩下(m+1)(r-1)个,以后保持这样的取法,那么先取者肯定获胜。总之,要保持给对手留下(m+1)的倍数,就能最后获胜。
作为一道小学生都会的数学题,相信......大家不会想问为什么。
Part 2 威佐夫博奕
问题模型:有两堆各若干个物品,两个人轮流从某一堆或同时从两堆中取同样多的物品,规定每次至少取一个,多者不限,最后取光者得胜。
解决思路:
A:设(ai,bi)(ai ≤bi ,i=0,1,2,…,n)表示两堆物品的数量并称其为局势
如果甲面对(0,0),那么甲已经输了,这种局势我们称为奇异局势。前几个奇异局势是:(0,0)、(1,2)、(3,5)、(4,7)、(6,10)、(8,13)、(9,15)、(11,18)、(12,20)。任给一个局势(a,b),如下公式判断它是不是奇异局势: ak =[k(1+√5)/2],bk= ak + k (k=0,1,2,…,n 方括号表示取整函数)。(证明见百度百科)
3、满足上公式的局势性质:
- 任何自然数都包含在一个且仅有一个奇异局势中。
由于ak是未在前面出现过的最小自然数,所以有ak > ak-1 ,而 bk= ak + k > ak-1 + k-1 = bk-1 > ak-1 。所以性质成立。
- 任意操作都可将奇异局势变为非奇异局势。
若只改变奇异局势(ak,bk)的某一个分量,那么另一个分量不可能在其他奇异局势中,所以必然是非奇异局势。如果使(ak,bk)的两个分量同时减少,则由于其差不变,且不可能是其他奇异局势的差,因此也是非奇异局势
采用适当的方法,可以将非奇异局势变为奇异局势。
假设面对的局势是(a,b),若 b = a,则同时从两堆中取走 a 个物体,就变为了奇异局势(0,0);如果a = ak ,b > bk,那么,取走b – bk个物体,即变 为奇异局势;如果 a = ak , b < bk ,则同时从两堆中拿走 ak – ab – ak个物体,变为奇异局势( ab – ak , ab – ak+ b – ak);如果a > ak , b= ak + k,则从第一堆中拿走多余的数量a – ak 即可;如果a < ak ,b= ak + k,分两种情况,第一种,a=aj (j < k),从第二堆里面拿走 b – bj 即可; 第 二种,a=bj (j < k),从第二堆里面拿走 b – aj 即可。
4、结论:两个人如果都采用正确操作,那么面对非奇异局势,先拿者必胜;反之,则后拿者取胜。


