树链剖分
前置知识
- LCA
- 树形DP
- DFS序
- 线段树
attention!!:线段树必须可以掌握且可以较为熟练地打出来(不然的话,嘿嘿嘿......)
树链剖分
在开始学习树链剖分之前,我们一定要明白:这个算法有什么用:
先回顾2个问题:
1,将树从x到y结点最短路径上所有节点的值都加上z
树上差分可以以O(n+m)的优秀复杂度解决这个问题
2,求树从x到y结点最短路径上所有节点的值之和
lca,dfs O(n)预处理每个节点的dis(即到根节点的最短路径长度)
然后对于每个询问,求出x,y两点的lca,利用lca的性质distance ( x , y ) = dis ( x ) + dis ( y ) - 2 * dis ( lca )求出结果
时间复杂度O(mlogn+n)
现在给出一个新问题:
将刚才的两个问题结合起来,
刚才的方法显然就不够优秀了(每次询问之前要跑dfs更新dis)
于是我们有了树链剖分这个算法,基本概念:
树链剖分,计算机术语,指一种对树进行划分的算法,它先通过轻重边剖分将树分为多条链,保证每个点属于且只属于一条链,然后再通过数据结构(树状数组、BST、SPLAY、线段树等)来维护每一条链。
再次前置知识:
- 重儿子:对于每一个非叶子节点,它的儿子中 以那个儿子为根的子树节点数最大的儿子 为该节点的重儿子
- 轻儿子:对于每一个非叶子节点,它的儿子中 非重儿子 的剩下所有儿子即为轻儿子
- 叶子节点没有重儿子也没有轻儿子(因为它没有儿子。。)
- 重边:一个父亲连接他的重儿子的边称为重边
- 轻边:剩下的即为轻边
- 重链:相邻重边连起来的 连接一条重儿子 的链叫重链
- 对于叶子节点,若其为轻儿子,则有一条以自己为起点的长度为1的链
- 每一条重链以轻儿子为起点
例题:
树链剖分 就是对一棵树分成几条链,把树形变为线性,减少处理难度
- 将树从x到y结点最短路径上所有节点的值都加上z
- 求树从x到y结点最短路径上所有节点的值之和
- 将以x为根节点的子树内所有节点值都加上z
- 求以x为根节点的子树内所有节点值之和
正题
预处理
第一次dfs:
- 标记每个点的深度dep
- 标记每个点的父亲fa
- 标记每个非叶子节点的子树大小(含它自己)
- 标记每个非叶子节点的重儿子编号son
第二次dfs:
-
标记每个点的新编号
-
赋值每个点的初始值到新编号上
-
处理每个点所在链的顶端
-
处理每条链
注意!进行第二次遍历时,一定要先遍历重儿子,再看轻儿子,原因的话,请继续看下去
在此引用洛谷中的dalao的图片(懒......)
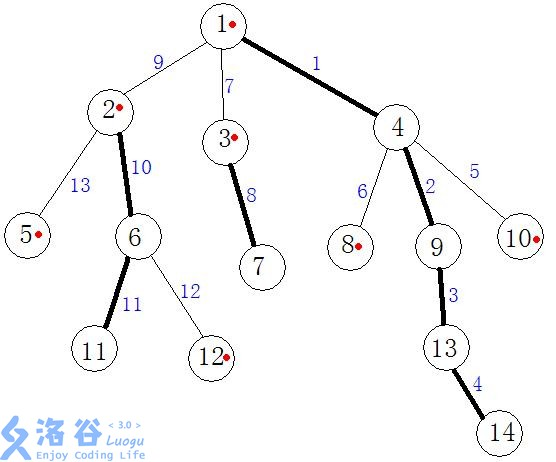
红点为重链的头,粗边为重链。
推送一下代码:
void dfs1(int u){
//设重儿子大小为-1,方便统计答案(会有为0的)
int mxu=-1;
for (int i=head[u];i;i=a[i].next){
int v=a[i].to;
if (v==fa[u])continue;
//遍历
fa[v]=u;
dep[v]=dep[u]+1;
//更新数值
dfs1(v);
if (siz[v]>mxu)
son[u]=v,mxu=siz[v];
siz[u]+=siz[v];
//回溯后统计
}
siz[u]++;
//这点很重要,子树大小要包括自己,后面进行区间更新叶节点时有用!!
return;
}
void dfs2(int u,int h){
//类似tarjan的时间戳
dfn[u]=++dfncnt;
sum[dfncnt]=su[u];
//映射,将当前点对应的值映射到dfs序中
top[u]=h;
//标记每一条重链的头
if (!son[u]) return;
//叶子节点不用进行扫描
dfs2(son[u],h);
//重儿子直接向下递归
for (int i=head[u];i;i=a[i].next){
int v=a[i].to;
if (v==son[u]||v==fa[u])continue;
//遍历
dfs2(v,v);
//轻儿子以自己为根
//再次说明一个特殊性质:DFS序中,重链相邻,且,相邻两条间由一条轻边链接。
//这就是先重后轻的好处
}
return;
}
在此,我们开始进行问题的解决:
1.路径的处理
设所在链顶端的深度更深的那个点为x点
-
ans加上x点到x所在链顶端 这一段区间的点权和
-
把x跳到x所在链顶端的那个点的父亲节点
-
继续执行这两个步骤,直到两个点处于一条链上,这时再加上此时两个点的区间和即可
原因:请自己思考(图如下:)
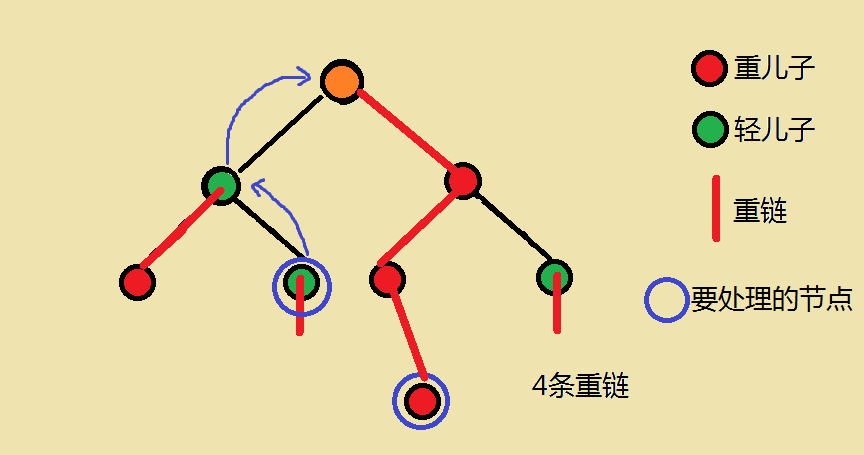
我们每次进行向上跳,每次跳一跳重链,一直跳下去的话,很显然可以发现这2点的LCA一定是重链上跳到达的点,原因:2条路径只有一个交点。
此时,我们将dfs序形成的数组用线段树维护信息。就可以用\(O(log^2n)\)查询路径信息,同时进行update(进行区间加或者乘)。
2.子树处理
这个时候,我们会发现一个非常美妙的性质:
以任意一点为根,注意:它的子树和他自己在dfs序中是连续的!!可以自己手动模拟数据看看(实在懒得画图,当然,你们可以喊jl老师画图,因为到时候我估计早就走了(😀))
基于这个非常美妙的性质,我们可以很快的维护子树,求值(因为啊,我们与处理了每个点的子树大小!!)
时间复杂度:O(\(log_2n\))
简单说明为什么连续:我们遍历dfs是逐步向下,将一整列遍历完之后看下一列,然后一级一级回溯,所以:子树在dfs序上自然是连续的,当然,画图最直观哈。
最后,推送一下代码:
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
using namespace std;
const int MAXN=1000005;
int n,m,r,p,tot,head[MAXN],sum[MAXN],su[MAXN];
int top[MAXN];
struct node{
int from,to,next;
}a[MAXN<<1];
struct Tree{
int l,r;
int laz,sum;
}t[MAXN<<1];
int dfn[MAXN],siz[MAXN];
int son[MAXN],dep[MAXN],fa[MAXN];
int dfncnt;
//线段树(我自己写的时候犯了以哦个小错:pushdown没把当天节点lazytag清零,然后......卡了5min,大家注意哦)
inline void build(int i,int l,int r){
t[i].l=l,t[i].r=r;
if (l==r){
t[i].sum=sum[l]%p;
return;
}
int mid=l+r>>1;
build(i<<1,l,mid);
build(i<<1|1,mid+1,r);
t[i].sum=t[i<<1].sum+t[i<<1|1].sum;
t[i].sum%=p;
}
void pushdown(int i){
t[i<<1].laz+=t[i].laz;
t[i<<1|1].laz+=t[i].laz;
t[i<<1].sum+=t[i].laz*(t[i<<1].r-t[i<<1].l+1)%p;
t[i<<1].sum%=p;
t[i<<1|1].sum+=t[i].laz*(t[i<<1|1].r-t[i<<1|1].l+1)%p;
t[i<<1|1].sum%=p;
t[i].laz=0;
return;
}
int res;
void query(int now,int L,int R){
if (t[now].l>=L&&t[now].r<=R){
res+=t[now].sum;
res%=p;
return;
}
else{
pushdown(now);
int mid=t[now].l+t[now].r>>1;
if (L<=mid) query(now<<1,L,R);
if (R>mid) query(now<<1|1,L,R);
}
return;
}
void update(int now,int L,int R,int k){
if (t[now].l>=L&&t[now].r<=R){
t[now].laz+=k;
t[now].sum+=k*(t[now].r-t[now].l+1);
t[now].sum%=p;
return;
}
else{
pushdown(now);
int mid=t[now].l+t[now].r>>1;
if (L<=mid) update(now<<1,L,R,k);
if (R>mid) update(now<<1|1,L,R,k);
t[now].sum=t[now<<1].sum+t[now<<1|1].sum;
t[now].sum%=p;
}
return;
}
//加边
void add(int u,int v){
a[++tot].next=head[u];
a[tot].to=v;
a[tot].from=u;
head[u]=tot;
}
//2遍预处理
void dfs1(int u){
int mxu=-1;
for (int i=head[u];i;i=a[i].next){
int v=a[i].to;
if (v==fa[u])continue;
fa[v]=u;
dep[v]=dep[u]+1;
dfs1(v);
if (siz[v]>mxu)
son[u]=v,mxu=siz[v];
siz[u]+=siz[v];
}
siz[u]++;
return;
}
void dfs2(int u,int h){
dfn[u]=++dfncnt;
sum[dfncnt]=su[u];
top[u]=h;
if (!son[u]) return;
dfs2(son[u],h);
for (int i=head[u];i;i=a[i].next){
int v=a[i].to;
if (v==son[u]||v==fa[u])continue;
dfs2(v,v);
}
return;
}
//查询路径
inline int range(int x,int y){
int ans=0;
while(top[x]!=top[y]){//一个一个向上跳
if (dep[top[x]]<dep[top[y]]) swap(x,y);//这只是为了在线段树维护写代码的l,r时方便
res=0;
query(1,dfn[top[x]],dfn[x]);//就是为了这里方便
ans+=res;
ans%=p;
x=fa[top[x]];//一定要跳到链头的父亲,不然会死循环。
}
if (dep[x]>dep[y])swap(x,y);
res=0;
query(1,dfn[x],dfn[y]);//最后在同一条重链上时,维护两点间的信息。
ans+=res;
return ans%p;//可以改成void直接输出,但是吧,这样好看,有针对性,尽量自己的函数只作处理,输出交给main,这样代码好读
}
//路径更新,这个的话.....和上面是一样的
inline void updrange(int x,int y,int k){
k%=p;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
update(1,dfn[top[x]],dfn[x],k);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
update(1,dfn[x],dfn[y],k);
return;
}
//子树求值
inline int qson(int x){
res=0;
query(1,dfn[x],dfn[x]+siz[x]-1);
return res;
}
//子树更新
inline void updson(int x,int k){
update(1,dfn[x],dfn[x]+siz[x]-1,k);
}
//由于子树dfs序连续性,真的非常好写!!!而且超快。
int main(){
//freopen (".in","r",stdin);
//freopen (".out","w",stdout);
scanf ("%d%d%d%d",&n,&m,&r,&p);
for (int i=1;i<=n;i++)
scanf ("%d",su+i);
int u,v;
for (int i=1;i<n;i++){
scanf ("%d%d",&u,&v);
add(u,v);
add(v,u);
}
dep[r]=1;
fa[r]=0;
dfs1(r);
dfs2(r,r);
build(1,1,n);
int c,x,y,z;
for (int i=1;i<=m;i++){
scanf ("%d%d",&c,&x);
if (c==1)
scanf ("%d%d",&y,&z),
updrange(x,y,z);
else if (c==2){
scanf ("%d",&y);
int ans=range(x,y);
printf ("%d\n",ans);
}
else if (c==3)
scanf ("%d",&z),
updson(x,z);
else{
int ans=qson(x);
printf ("%d\n",ans);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号