浅谈卡特兰数

定义

先给一个通项公式 \(Cat(n)=\frac{C_{2n}^{n}}{n+1}\)。

卡特兰数是一个比较通用的模型，有很多的问题都与其有关，其中比较经典的是括号序列计数和二叉树计数。

经典的问题

一些描述

括号序列计数

给定 \(n\)，求有多少个合法的长度为 \(2n\) 的括号序列。

二叉树计数

给定 \(n\)，求有多少个合法的 \(n\) 个节点的二叉树。

朴素的做法

考虑 dp。

括号序列计数

先抽象一下问题，把 \((\) 抽象为 \(1\)， \()\) 抽象为 \(-1\)，我们设一个括号序列的对应值为抽象成数字后的序列的和，而合法的括号序列就要满足这个序列的所有前缀和都要是非负的，zu

设 \(dp_{i}\) 表示长度为 \(i\) 的合法括号序列个数，根据序列中第一个 \((\)，枚举对应的 \()\) 括起来的范围，可以把这个序列分成 2 个部分，如下图：

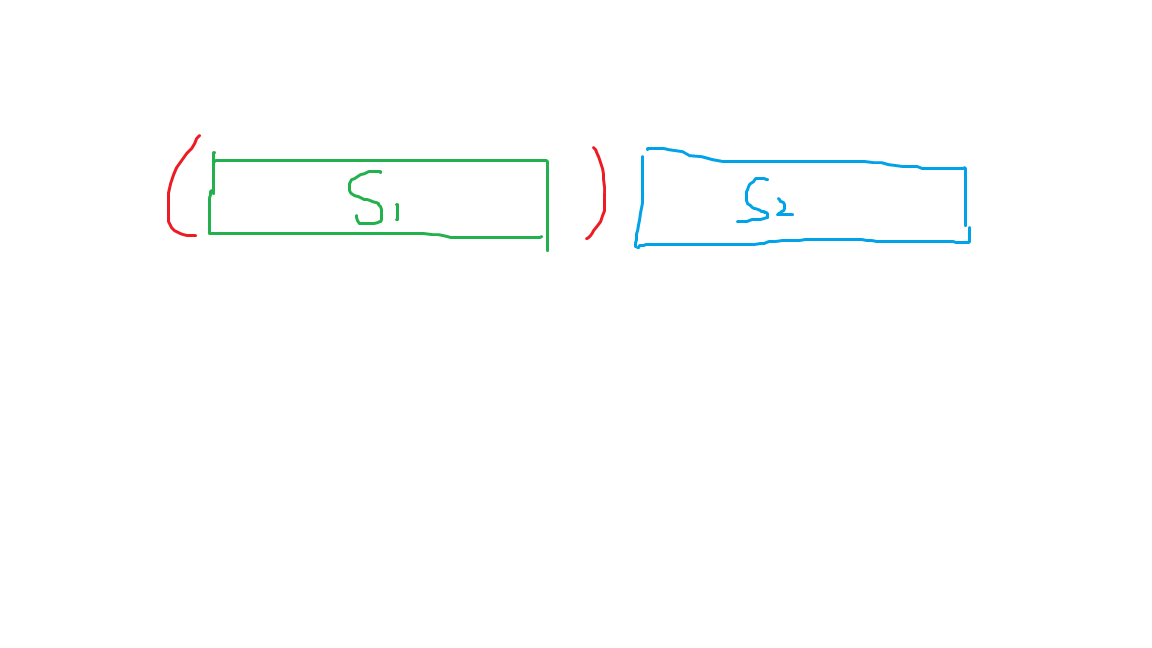
可以看到，上文提到的两部分分别是 \(s_1\) 和 \(s_2\)，显然，整个序列要是合法的，要求 \(s_1\)，\(s_2\) 也是合法的，发现就是子问题了，可以直接 dp 做。

\(dp_i=\sum_{j=1}^i {dp_{i-j}\times dp_{j-1}}\)

二叉树计数

同上， \(dp_i\) 表示的是以 \(i\) 个节点的二叉树个数，显然通过二叉还是可以分成 2 部分，然后转移和上面的就一样了。

数学的做法

以括号序列为例，我们建立一个数学模型，考虑有后效性的东西，只有他们的对应值，发现对应值其实也是左括号和右括号的个数，发现是两维的，考虑把这个东西建立在平面直角坐标系上面，抽象成走路径问题，起点是 \((0,0)\)，终点是 \((n,n)\)，要求合法，所以左括号个数必须一直比右括号个数多，即 \(x\geq y\)，转换为数学语言就是这条路径不能经过 \(y=x+1\) 这个函数。

至于为什么是 \(y=x+1\),因为 \(y=x\) 也是合法的，所以往上走一格判断不合法。

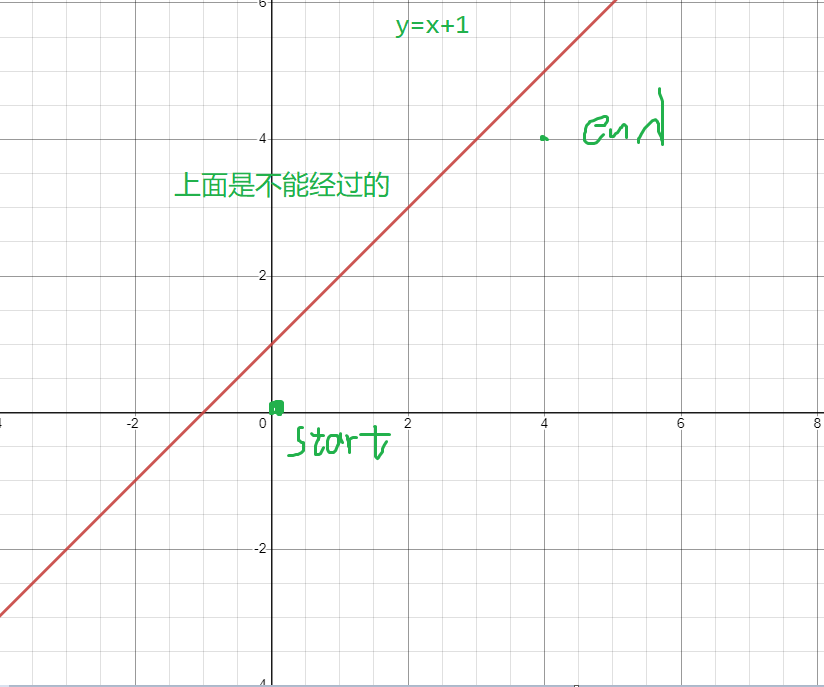
发现不好做，这个时候就可以使用第一个经典的技巧，正难则反，考虑用所有的情况减去不合法的情况，不合法的情况就是经过了 \(y=x+1\) 的情况，发现可以经过很多次，于是可以使用第二个技巧，使用标志物，把统计经过这条直线变成第一次经过这条直线的方案，发现还是不好统计，所以就请出第三个技巧，找双射，找到一个对应的情况，但是更好统计，比如上面的问题，就可以这样子搞：

考虑第一次过那条线的点，把路径以 \(y=x+1\) 为对称轴翻折上去，没错，就像将军饮马一样，这样子折线就被我们变成了直线，我们只需要把起点翻过去，在考虑新的起点到本来的终点的方案数量就是不合法的方案数量了。

翻着上去，起点是 \((-1,1)\)，一共走 \(2n\) 步，选 \(n-1\) 步往上走，所以一共的方案就是 \(C_{2n}^{n-1}\)，所以合法方案数量就是 \(C_{2n}^{n}-C_{2n}^{n}\) 套公式化简以下就是 \(\frac{C_{2n}^{n}}{n-1}\)，这就是著名的卡特兰数。
二叉树计数是类似的，就不写了。

卡特兰数本身不难，但是一些看似没有关系的问题恰好就是卡特兰数的变形，学习卡特兰数让我学到了三个排列组合的技巧。

首先就是正难则反，一定有一个方向是不难的，其二是对于容易统计重复的东西，我们给他一个标志物，比如第一次，一定等等，其三就是找双射，让每一种方案都有对应的方案，而对应的方案更好统计。

对于有 2 个有后效性的东西，我们可以考虑放在平面直角坐标系上进行统计，就是数形结合，这些技巧都是很有用的。