二分图和 2-SAT 问题入门
二分图
定义
通俗的说,就是一个图可以分成两个部分,两个部分内部没有连接的边,所有的边都在两个部分之间。
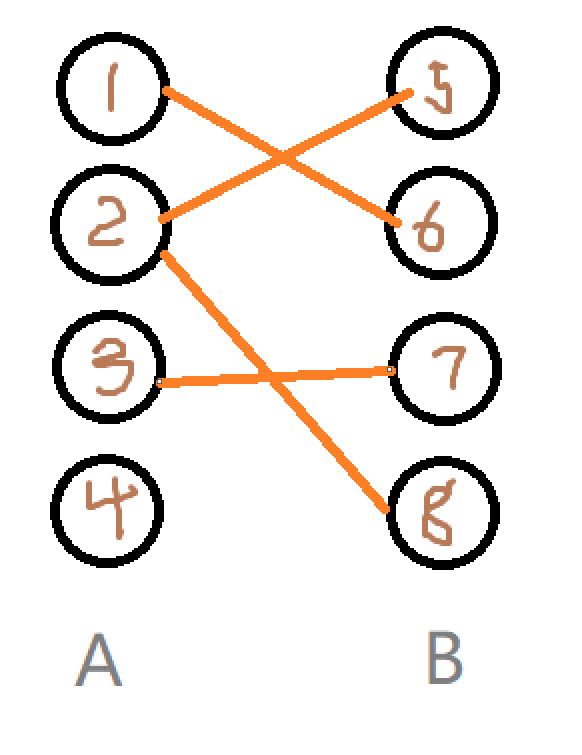
比如这就是一张二分图。可以发现,A,B集合中各自是没有边连接的,边都连在了 A B 集合之间。并且 4 是独立的,所以其实我们把它归到集合 A 中或者集合 B 中都可以。
判断二分图
就是一个判断一个图是不是二分图的方法。我们可以通过染色来判断二分图,如上面的例子中, A 可以染一种颜色, B 可以染另一种颜色。
做法就是用 dfs, 一边递归一边染色,相邻的两个点染的颜色应该是不同的,否则就违反了二分图的定义。颜色可以抽象成 0 和 1。
具体的来讲:
设当前的点是 \(u\),它的颜色是 \(s\),下一个点是 \(v\),如果当前这个点没有染色,我们就把它染成 \(s\ \mathbb{xor}\ 1\) 的颜色,如果当前这个点已经染色了并且染的是 \(s\mathbb{xor}\ 1\),就不管它,如果已经染色成了 \(s\),就说明出现了冲突,这张图一定不是二分图。
std::vector<int> G[N];
int c[N];
void dfs(int u, int co) {
c[u] = co;
for (auto v : G[u]) {
if (c[v] == -1) {
dfs(v, co ^ 1);
}
if (c[v] != -1 && c[v] == co) {
std::cout << "No\n";
exit(0);
}
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
int n, m;
std::cin >> n >> m;
memset(c, -1, sizeof c);
for (int i = 0; i < m; i++) {
int u, v;
std::cin >> u >> v;
G[u].push_back(v);
}
for (int i = 1; i <= n; i++) {
if (c[i] == -1) {
dfs(i, 0);
}
}
std::cout << "Yes";
return 0;
}
其中的 c 数组就是二分图的分布了,0 的是一个集合,1 的是一个集合。
二分图匹配
匹配问题,给出一个二分图,求有多少个左边的点可以找到一个右边的点,满足右边的点没有被其他左边的点选择,并且这两个点之间有一条边连接。
可以理解为男生女生找朋友的问题,左边是男生,右边是女生,中间连的边可以理解成有可能在一起,所以这个问题就是求按照这样匹配最终最多可以形成多少对情侣。
匈牙利算法
就像暴力一样,我们对每一个左边的点进行考虑,找到它连接到右边的点中没有被选择的点选择,与它如果所有连接的点都被选择了,就可以每个点尝试匹配给它,而之前匹配那个点的左边的点匹配另一个,直到最后所有的左边的点都被匹配完毕,这就是一个最多匹配的方案。
听起来很难,其实通过简单的递归就可以达到这个效果。
我们先定义一下这个递归的意义:bool dfs(u) 表示 u 是否能被匹配。
对于这个函数,我们先扫描所有 u 的出边,如果一条出边的点没有被选择,我们就可以选择,并且把这个点进行标记。同时,如果这条出边的点已经被选择了,但是匹配上这个点的左边的点可以匹配上不是这个点的其他的点,那我们也可以让这个点给现在考虑的点,把之前这个点对应的点分配给另一个。发现这个问题中出现了重复,就是在求解这个点对应点是否可以匹配上其他点的这个问题就是 dfs 的定义。
于是我们就可以对每个点都进行 dfs 进行分配。
注意,这里还要用一个 vis 数组,在每次 dfs 开始的时候都要把这个 vis 数组清零,这个数组意义在于防止一些匹配的点再次被匹配的死循环的情况出现。
每次都 memset 肯定是不好的,所以这里有个有点聪明的小优化,在不同的 dfs 上给 vis 数组赋上不同的值,就可以避免浪费时间,虽然这个优化 p 用没有。
int n, n1, m, u, v;
int vis[N];
int ma[N];
int dfs(int u, int s) {
if (vis[u] == s) {
return 0;
}
vis[u] = s;
rep_edges (i, u) {
if (!ma[v] || dfs(ma[v], s)) {
ma[v] = u;
return 1;
}
}
return 0;
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
std::cin >> n >> n1 >> m;
std::map<std::array<int, 2>, int> used;
for (int i = 0; i < m; i++) {
std::cin >> u >> v;
if (!used[{u, v}]) {
used[{u, v}] = 1;
add(u, v);
}
}
int ans = 0;
for (int i = 1; i <= n; i++) {
ans += dfs(i, i);
}
std::cout << ans << '\n';
return 0;
}
2-SAT 问题
定义
先讲一下什么是 SAT 问题。
要求你构造一个数组,要求满足若干的形如 \(x_1 || x_2 = \mathbb{true}\) 的关系,左边是若干个数组中的元素,它们的运算是与和或,右边是 \(\mathbb{true}\) 或者 \(\mathbb{false}\) 。
而 2-SAT 问题就是等式左边有且仅有 \(2\) 个元素的 SAT 问题。比如 \(x_1 || x_2 || x_3 = \mathbb{false}\) 就不是一个 2-SAT 问题。
顺便一提, SAT 问题只能暴力。
算法
这个题可以用图论做
把每个数组里的数抽象成两个点,一个点表示这个数是 \(1\), 一个点表示这个数是 \(0\),显然一个数只能是一种情况,所以它们就属于两个不同的集合,而我们要在这两个集合里面选出 \(n\) 个数。
但是怎么满足上面的条件呢?可以分类讨论一下,这里我们就分与和或讨论:
- 与
为了方便表述,我这里定义两个需要确定是 0 还是 1 的点 \(a, b\),用 \(a_{0}\) 来表示 a 是 0 的情况,用 \(a_{1}\) 来表示 a 是 1 的情况, \(b\) 也是同理。
- \(a\) \(\texttt{&&}\) \(b = true\)
显然当 \(a\) 是 0 的时候无论如何都不能使它为 1,我们就可以连一条从 \(a_{0}\) 到 \(a_{1}\) 的边,这样无论如何都可以让 \(a\) 是 1, \(b\) 也是同理。
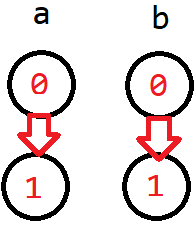
- \(a\) \(\texttt{&&}\) \(b = false\)
显然当 \(a\) 是 1 的时候 \(b\) 只能是 0, 相反,当 \(b\) 是 1 的时候, \(a\) 只能是 0,所以我们就可以连 \(a_1\) 到 \(b_0\) 和 \(b_1\) 到 \(a_0\)。
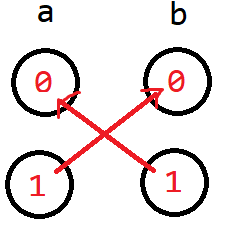
- 或
- \(a || b = false\)
可以发现这里 \(a\) 和 \(b\) 都只能是 0,所以就和上面的与的第一种情况一样了。
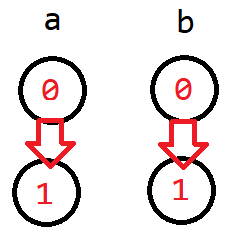
- \(a || b = true\)
当 \(a\) 是 0 时, \(b\) 只能是 1 ,反之,当 \(b\) 是 0 时,\(a\) 只能是 1,所以就像上面与的第二种情况一样连接即可,具体看下面的图:
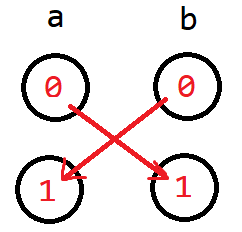
就这样,你得到一张有向图。
考虑无解的情况,可以发现当一个点的 true 和 false 在同一个强连通分量中时就时无解的。
考虑有解怎么做,可以发现我们应该优先选取被指向的点,而不是指向其他点的点,因为指向其他点的点可能会造成无解。于是在拓扑排序的意义下,就是拓扑序比较大的那个值。同时可以发现在同一个强连通分量中的点都是要么选要么不选的,于是我们要用 tarjan 缩一下点。
难道我们还需要用拓扑排序求谁的拓扑序更大?其实是不用的,可以想一下,拓扑序越大的应该时越接近于叶子节点的, 而 tarjan 缩点的顺序应该是先从叶子节点缩的,所以 tarjan 定的缩的点的序号越小就说明这个点的拓扑序越大,所以就不用拓扑排序求了。
算法的瓶颈在于 tarjan,所以时间复杂度是 \(\mathbb{o}{(n+m)}\)。
// Code by 落花月朦胧.
#include <bits/stdc++.h>
using i64 = long long;
constexpr int iinf = 1E9;
constexpr i64 linf = 1E18;
// 克鲁鲁 克鲁鲁 克鲁鲁 克鲁鲁 克鲁鲁 克鲁鲁 克鲁鲁 克鲁鲁
constexpr int N = 3E6 + 10;
constexpr int P = 998244353;
i64 power(i64 a, i64 b, i64 p) {
i64 res = 1;
for (; b; b >>= 1, a = (a * a) % p)
if (b & 1) res = (res * a) % p;
return res % p;
}
int timer;
int dfn[N], low[N], scc[N], SCC;
int op[N], in[N];
int color[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
int n, m;
std::cin >> n >> m;
std::vector<int> G[(n << 1) + 10];
#define add(a, b) G[a].push_back(b)
for (int i = 1; i <= m; i++) {
// a 是 b 的 或者 c 是 d 的
int a, b, c, d;
std::cin >> a >> b >> c >> d;
add(a + (b ^ 1) * n, c + d * n);
add(c + (d ^ 1) * n, a + b * n);
}
// tarjan.
std::stack<int> s;
std::function<void(int)> tarjan = [&](int u) {
dfn[u] = low[u] = ++timer;
s.push(u);
for (auto v : G[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = std::min(low[u], low[v]);
} else if (!scc[v]) {
low[u] = std::min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
SCC++;
scc[u] = SCC;
while (s.top() != u) {
scc[s.top()] = SCC;
s.pop();
}
s.pop();
}
};
for (int i = 1; i <= n * 2; i++) {
if (!dfn[i]) {
tarjan(i);
}
if (i <= n && scc[i] == scc[i + n]) {
std::cout << "IMPOSSIBLE\n";
return 0;
}
}
std::cout << "POSSIBLE\n";
for (int i = 1; i <= n; i++) {
std::cout << (scc[i] > scc[i + n]) << ' ';
}
std::cout << '\n';
return 0;
}
这里还有一道模板题。这个题我就用了拓扑排序求更大的拓扑序,并且这份代码中的 0 和 1 我所规定的顺序是不一样的,这些写法其实都是可以的,所以这里放出来当一个参考。
这是上面的代码的编号方式
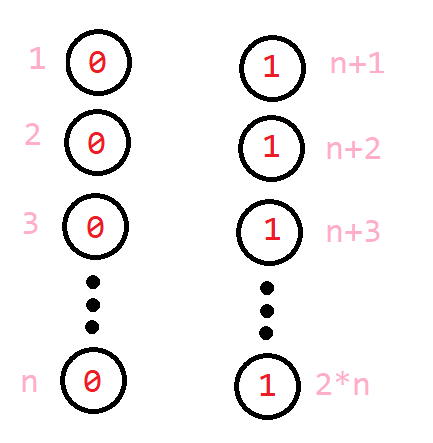
这是下面的代码的命名方式
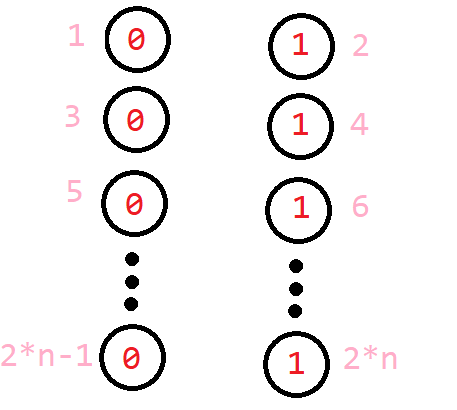
其实各有好处,主要看题目怎么要求的。
// Code by 落花月朦胧.
#include <bits/stdc++.h>
using i64 = long long;
constexpr int iinf = 1E9;
constexpr i64 linf = 1E18;
// 克鲁鲁 克鲁鲁 克鲁鲁 克鲁鲁 克鲁鲁 克鲁鲁 克鲁鲁 克鲁鲁
constexpr int N = 3E6 + 10;
constexpr int P = 998244353;
i64 power(i64 a, i64 b, i64 p) {
i64 res = 1;
for (; b; b >>= 1, a = (a * a) % p)
if (b & 1) res = (res * a) % p;
return res % p;
}
int timer;
int dfn[N], low[N], scc[N], SCC;
int op[N], in[N];
int color[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
int n, m;
std::cin >> n >> m;
std::vector<int> G[(n << 1) + 10];
for (int i = 1; i <= m; i++) {
int u, v;
std::cin >> u >> v;
if (v & 1) {
G[u].push_back(v + 1);
} else {
G[u].push_back(v - 1);
}
if (u & 1) {
G[v].push_back(u + 1);
} else {
G[v].push_back(u - 1);
}
}
// tarjan.
std::stack<int> s;
std::function<void(int)> tarjan = [&](int u) {
dfn[u] = low[u] = ++timer;
s.push(u);
for (auto v : G[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = std::min(low[u], low[v]);
} else if (!scc[v]) {
low[u] = std::min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
SCC++;
scc[u] = SCC;
while (s.top() != u) {
scc[s.top()] = SCC;
s.pop();
}
s.pop();
}
};
for (int i = 1; i <= n * 2; i++) {
if (!dfn[i]) {
tarjan(i);
}
}
for (int i = 0; i < n; i++) {
int nexta = i << 1, nextb = i << 1 | 1;
nexta++; nextb++;
if (scc[nexta] == scc[nextb]) {
std::cout << "NIE\n";
return 0;
}
op[scc[nexta]] = scc[nextb];
op[scc[nextb]] = scc[nexta];
}
std::vector<int> g[SCC + 1];
for (int u = 1; u <= n * 2; u++) {
for (auto v : G[u]) {
if (scc[v] != scc[u]) {
g[scc[v]].push_back(scc[u]);
in[scc[u]]++;
}
}
}
// topu.
std::queue<int> q;
for (int i = 1; i <= SCC; i++) {
if (!in[i]) {
q.push(i);
}
}
while (q.size()) {
int u = q.front(); q.pop();
if (!color[u]) {
color[u] = 2;
color[op[u]] = 1;
}
for (auto v : g[u]) {
if (!--in[v]) {
q.push(v);
}
}
}
std::vector<int> ans;
for (int i = 1; i <= SCC; i++) {
if (color[i] == 2) {
for (int j = 1; j <= n * 2; j++) {
if (scc[j] == i) {
ans.push_back(j);
}
}
}
}
std::sort(ans.begin(), ans.end());
for (auto v : ans) {
std::cout << v << "\n";
}
return 0;
}
写作不易,点个赞吧 qaq。


