20230122寄

新年快乐！

早上 8：00起来的，起来就打了4个小时游戏来庆祝新年。

水的题

P2846 [USACO08NOV]Light Switching G

线段树板子题，复习了一下。

#include <bits/stdc++.h>
 
using i64 = long long;
constexpr int N = 1E5 + 10;
 
struct T {
    int val, tag;
    int l, r;
    void update() {
        val = (r - l + 1) - val;
    }
} t[N << 2];
 
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
void build(int l, int r, int rt) {
    t[rt].l = l; t[rt].r = r;
    if (l == r) {
        return;
    }
    int mid = (l + r) / 2;
    build(lson);
    build(rson);
}
 
void pushup(int rt) {
    t[rt].val = t[rt << 1].val + t[rt << 1 | 1].val;
}
 
void pushdown(int rt) {
    if (t[rt].tag) {
        t[rt << 1].tag ^= t[rt].tag;
        t[rt << 1 | 1].tag ^= t[rt].tag;
        t[rt << 1].update();
        t[rt << 1 | 1].update();
        t[rt].tag = 0;
    }
}
 
void update(int L, int R, int rt) {
    if (L <= t[rt].l && t[rt].r <= R) {
        t[rt].update();
        t[rt].tag ^= 1;
        return;
    }
    pushdown(rt);
    int mid = (t[rt].l + t[rt].r) / 2;
    if (L <= mid) {
        update(L, R, rt << 1);
    }
    if (R > mid) {
        update(L, R, rt << 1 | 1);
    }
    pushup(rt);
}
 
int query(int L, int R, int rt) {
    if (L <= t[rt].l && t[rt].r <= R) {
        return t[rt].val;
    }
    pushdown(rt);
    int mid = (t[rt].l + t[rt].r) / 2, ans = 0;
    if (L <= mid) {
        ans += query(L, R, rt << 1);
    }
    if (R > mid) {
        ans += query(L, R, rt << 1 | 1);
    }
    return ans;
}
 
void out(int rt) {
    if (t[rt].l == t[rt].r) {
        std::cout << t[rt].val << " ";
        return;
    }
    out(rt << 1);
    out(rt << 1 | 1);
}
 
int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
 
    int n, m;
    std::cin >> n >> m;
 
    build(1, n, 1);
    for (int i = 0; i < m; i++) {
        int op, l, r;
        std::cin >> op >> l >> r;
        if (!op) {
            update(l, r, 1);
        } else {
            std::cout << query(l, r, 1) << "\n";
        }
    }
    
    return 0;
}

P2574 XOR的艺术

发现和上一个题是一样的，但是多了一个读入操作，随便看看，我并没有意识到问题的严重性。

写完了一交，0分，甚至过了样例。

经过了20分钟的罚坐后发现了问题是 build 函数里面没有 pushup，/kk 怎么办太蔡了。

P3130 [USACO15DEC] Counting Haybale P

板子线段树。

#include <bits/stdc++.h>
 
using i64 = long long;
constexpr int N = 2E5 + 10;
#define val(x) t[x].val
#define add(x) t[x].add
#define mn(x) t[x].mn
#define l(x) t[x].l
#define r(x) t[x].r
#define siz(x) t[x].siz
 
struct T {
    i64 val, add, mn;
    int l, r, siz;
} t[N << 2];
 
void pull(int rt) {
    val(rt) = val(rt << 1) + val(rt << 1 | 1);
    mn(rt) = std::min(mn(rt << 1), mn(rt << 1 | 1));
}
void build(int l, int r, int rt) {
    l(rt) = l; r(rt) = r; siz(rt) = r - l + 1;
    mn(rt) = 1E15; add(rt) = 0;
    if (l == r) {
        std::cin >> val(rt);
        mn(rt) = val(rt);
        return ;
    }
    int mid = (l + r) / 2;
    build(l, mid, rt << 1);
    build(mid + 1, r, rt << 1 | 1);
    pull(rt);
}
void pushdown(int rt) {
    if (add(rt)) {
        add(rt << 1) += add(rt);
        add(rt << 1 | 1) += add(rt);
        val(rt << 1) += (siz(rt) - siz(rt) / 2) * add(rt);
        val(rt << 1 | 1) += siz(rt) / 2 * add(rt);
        mn(rt << 1) += add(rt);
        mn(rt << 1 | 1) += add(rt);
        add(rt) = 0;
    }
}
 
void update(int L, int R, i64 x, int rt) {
    if (L <= l(rt) && r(rt) <= R) {
        val(rt) += siz(rt) * x;
        mn(rt) += x;
        add(rt) += x;
        return ;
    }
    pushdown(rt);
    int mid = (l(rt) + r(rt)) / 2;
    if (L <= mid) {
        update(L, R, x, rt << 1);
    }
    if (R > mid) {
        update(L, R, x, rt << 1 | 1);
    }
    pull(rt);
}
i64 query_sum(int L, int R, int rt) {
    if (L <= l(rt) && r(rt) <= R) {
        return val(rt);
    }
    pushdown(rt);
    int mid = (l(rt) + r(rt)) / 2;
    i64 ans = 0ll;
    if (L <= mid) {
        ans += query_sum(L, R, rt << 1);
    }
    if (R > mid) {
        ans += query_sum(L, R, rt << 1 | 1);
    }
    return ans;
}
i64 query_mn(int L, int R, int rt) {
    if (L <= l(rt) && r(rt) <= R) {
        return mn(rt);
    }
    pushdown(rt);
    int mid = (l(rt) + r(rt)) / 2;
    i64 ans = LONG_LONG_MAX;
    if (L <= mid) {
        ans = std::min(ans, query_mn(L, R, rt << 1));
    }
    if (R > mid) {
        ans = std::min(ans, query_mn(L, R, rt << 1 | 1));
    }
    return ans;
}
 
int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int n, m;
    std::cin >> n >> m;
 
    build(1, n, 1);
 
    while (m--) {
        char op; int l, r;
        std::cin >> op >> l >> r;
        if (op == 'P') {
            int x;
            std::cin >> x;
            update(l, r, x, 1);
        }
        if (op == 'S') {
            std::cout << query_sum(l, r, 1) << "\n";
        }
        if (op == 'M') {
            std::cout << query_mn(l, r, 1) << "\n";
        }
    }
 
    return 0;
}

P3870 [TJOI2009] 开关

一个题。

P4086 [USACO17DEC]My Cow Ate My Homework S

水题，for 一遍就完了，但是为什么有线段树的标签（恼。

P1160 队列安排

list 练习题。 但是没学过，现学现用（本质：ctj

#include <bits/stdc++.h>
 
using i64 = long long;
using Iter = std::list<int>::iterator;
 
 
Iter p[100010];
int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int N;
    std::cin >> N;
 
    std::list<int> l;
    l.push_front(1);
    p[1] = l.begin();
    for (int i = 2; i <= N; i++) {
        int a, b;
        std::cin >> a >> b;
        if (!b) {
            p[i] = l.insert(p[a], i);
        } else {
            auto nxt = next(p[a]);
            p[i] = l.insert(nxt, i);
        }
    }
 
    int M;
    std::cin >> M;
 
    std::map<int, int> mp;
    for (int i = 0; i < M; i++) {
        int x;
        std::cin >> x;
        mp[x] = 1;
    }
 
    for (auto v : l) {
        if (!mp[v]) {
            std::cout << v << " ";
        }
    }
    std::cout << "\n";
 
    return 0;
}

P1476 休息中的小呆

题目就像依托答辩，鬼知道讲了什么，搜了一下原题，结果原题是从 $1 \to n-1$ 的路径有哪些，最短距离是多少。

Floyd 就过了。

P1661 扩散

连通块显然并查集。

答案具有单调性，大于这个值的答案一定可以，所以就二分一下。

分析一下就可以发现扩散控制的是曼哈顿距离，由于两个点是同时扩散的，所以两个点之间时间就是曼哈顿距离除 2。

二分就直接二分时间，并查集查一下这个时间满不满足所有点成一个连通块。

#include <bits/stdc++.h>
 
using i64 = long long;
 
struct DSU {
    std::vector<int> f, siz;
    DSU(int n) : f(n), siz(n, 1) { std::iota(f.begin(), f.end(), 0); }
    int leader(int x) {
        while (x != f[x]) x = f[x] = f[f[x]];
        return x;
    }
    bool same(int x, int y) { return leader(x) == leader(y); }
    bool merge(int x, int y) {
        x = leader(x);
        y = leader(y);
        if (x == y) return false;
        siz[x] += siz[y];
        f[y] = x;
        return true;
    }
    int size(int x) { return siz[leader(x)]; }
};
int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    
    int n;
    std::cin >> n;
 
    std::vector<int> x(n), y(n);
    for (int i = 0; i < n; i++) {
        std::cin >> x[i] >> y[i];
    }
 
    auto check = [&](int X) -> bool {
        DSU d(n);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (std::abs(x[i] - x[j]) + std::abs(y[i] - y[j]) <= X * 2) {
                    d.merge(i, j);
                }
            }
        }
        return d.size(0) == n;
    };
 
    int l = 0, r = 1E9;
    while (l <= r) {
        int mid = (l + r) / 2;
        if (check(mid)) {
            r = mid - 1;
        } else {
            l = mid + 1;
        }
    }
 
    std::cout << l << '\n';
 
    return 0;
}

P1305 新二叉树

水题。

复习的算法

LCA

这个sb已经什么都不记得了。

LCA就是最近公共祖先，就定义完了。

首先就是有一个暴力的做法，两个点往上跳，第一个交点就是 lca，显然，时间复杂度为 $\mathcal{O(n)}$ 的，有没有更好的做法。

倍增 LCA 就是一个比较合理的做法，因为基于倍增，这个做法的时间复杂度就是 $\mathcal{O(\log n)}$ 的，有很大的优化。

倍增的话就是先让他们的深度相同，然后在一起跳，跳就用了倍增的思想。

首先我们要预处理一些东西：深度， $\log$ ，还有就是一个神秘的 $f_{i, j}$

深度随便 dfs 一下就好了。

$\log$ 可以用 cmath 里面的函数，但是常数就会变大，我们可以线性预处理一下，方法很多，这里有一种

rep (i, 1, n) {
	lg[i] = lg[i - 1] + (1 << lg[i - 1] == n);
}

重点就是这个 $f_{i, j}$ ，这个东西表示 $i$ 的节点的 $2^{j}$ 的祖先是谁。

这个东西也可以在 dfs 里面求。

初始化的话就是 $f_{i, 0}=fa$ ，显然。

然后就是lca里面最重要的一步

rep (i, 1, lg[dep[u]]) {
	f[u][i] = f[f[u][i - 1]][i - 1];
}

也就是说 $u$ 的 $2^i$ 祖先 = ($u$ 的 $2^{i-1}$ 祖先) 的 $2^{i-1}$ 祖先 $\to$ $2^i=2^{i-1+1}=2^{i-1}\times 2=2^{i-1}+2^{i-1}$

不仅是正确的，同时也是从前面的部分推过来的，有 $dp$ 的思想。

然后就是跳的过程了，我们从大到小的跳，如果大了跳不了就跳小的，就是倍增的思想，同时一定是可以跳到的，因为一个数一定可以分解成 $2^i$ 的和的形式

int lca(int x, int y) {
    if (dep[x] < dep[y])
        std::swap(x, y);
    while (dep[x] > dep[y])
        x = par[x][lg[dep[x] - dep[y]] - 1];
    if (x == y) return x;
    per (k, lg[dep[x]] - 1, 0) if (par[x][k] != par[y][k]) {
        x = par[x][k];
        y = par[y][k];
    }
    return par[x][0];
}

lca的题

事实上是看到了这个题才去学的 lca

P3884 [JLOI2009]二叉树问题

随便写一下套一下板子就过了。

#include <bits/stdc++.h>
#define rep(i, x, y) for (int i = (x); i <= (y); i++)
#define per(i, x, y) for (int i = (x); i >= (y); i--)
using i64 = long long;
constexpr int iinf = 1E9;
constexpr i64 linf = 1E18;
constexpr int N = 200;
 
int n, u, v;
std::vector<int> G[N];
int dep[N], par[N][20], lg[N];
std::map<int, int> mp;
 
void dfs(int u, int fa) {
    dep[u] = dep[fa] + 1, par[u][0] = fa;
    rep (i, 1, lg[dep[u]])
        par[u][i] = par[par[u][i - 1]][i - 1]; // (u) 的 2^i 祖先 = (u 的 2^(i-1) 祖先) 的 2^(i-1) 祖先 -> 2^i=2^(i-1+1)=(2^(i-1))*2=2^(i-1)+2^(i-1)
    for (auto v : G[u]) if (v != fa)
        dfs(v, u);
}
 
int lca(int x, int y) {
    if (dep[x] < dep[y])
        std::swap(x, y);
    while (dep[x] > dep[y])
        x = par[x][lg[dep[x] - dep[y]] - 1];
    if (x == y) return x;
    per (k, lg[dep[x]] - 1, 0) if (par[x][k] != par[y][k]) {
        x = par[x][k];
        y = par[y][k];
    }
    return par[x][0];
}
 
int main() {
    scanf("%d", &n);
    rep (i, 1, n - 1) {
        scanf("%d%d", &u, &v);
        G[u].push_back(v);
        G[v].push_back(u);
    }
    rep (i, 1, n) lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
    dfs(1, 0);
 
    int ans1 = -1, ans2 = -1;
    rep (i, 1, n) {
        ans1 = std::max(ans1, dep[i]);
        mp[dep[i]]++;
    }
    for (auto v : mp) {
        ans2 = std::max(ans2, v.second);
    }
    printf("%d\n%d\n", ans1, ans2);
 
 
    // ask
    scanf("%d%d", &u, &v);
    int is = lca(u, v), ans3 = 0;
    while (u != is) {
        u = par[u][0];
        ans3 += 2;
    }
    while (v != is) {
        v = par[v][0];
        ans3++;
    }
    printf("%d\n", ans3);
 
    return 0;
}

ST 表

复杂度
预处理 $\mathcal{O(n\log n)}$
查询 $\mathcal{O(1)}$

$f_{i, j}$ 表示从第 $i$ 个开始 $2^j$ 个范围内的最大值或者最小值。

然后求的话建议使用画图法来理解。

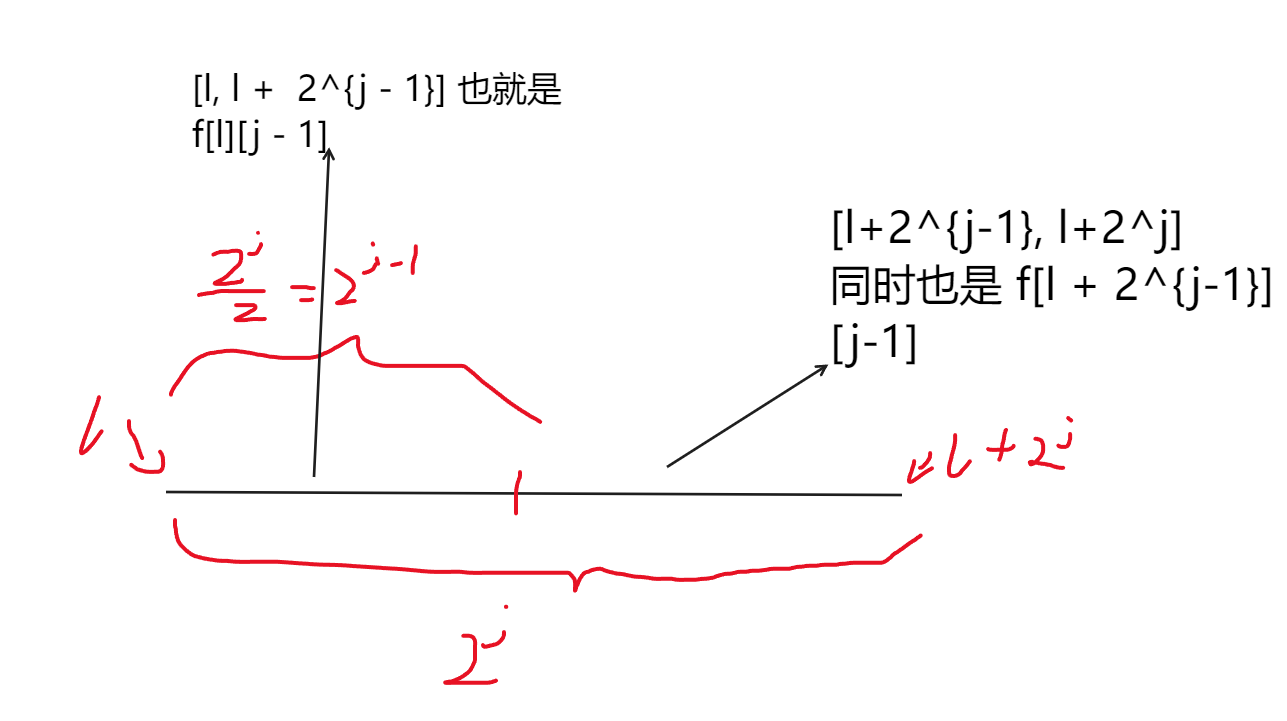
然后就理解完了，直接 dp 求一下就可以了。

查询也是一样的画图来理解。

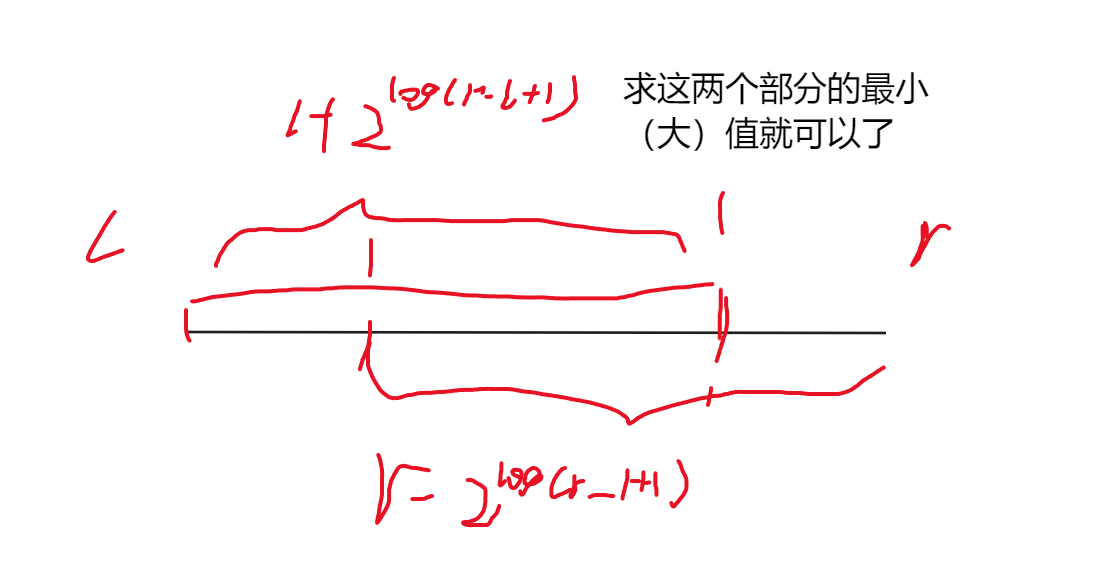
显然就是 $f_{l, log2(r - l + 1)}, f_{r - log2(r - l + 1)+1, log2(r - l + 1)}$

就做完了。