CF1642A Hard Way 题解

题目大意：

给出一个三角形，求不完全的线的长度。

不安全的定义是指从 \(x\) 轴上没有一个点满足：这个点和被检验的点所连接的直线不穿过这个三角形的内部。

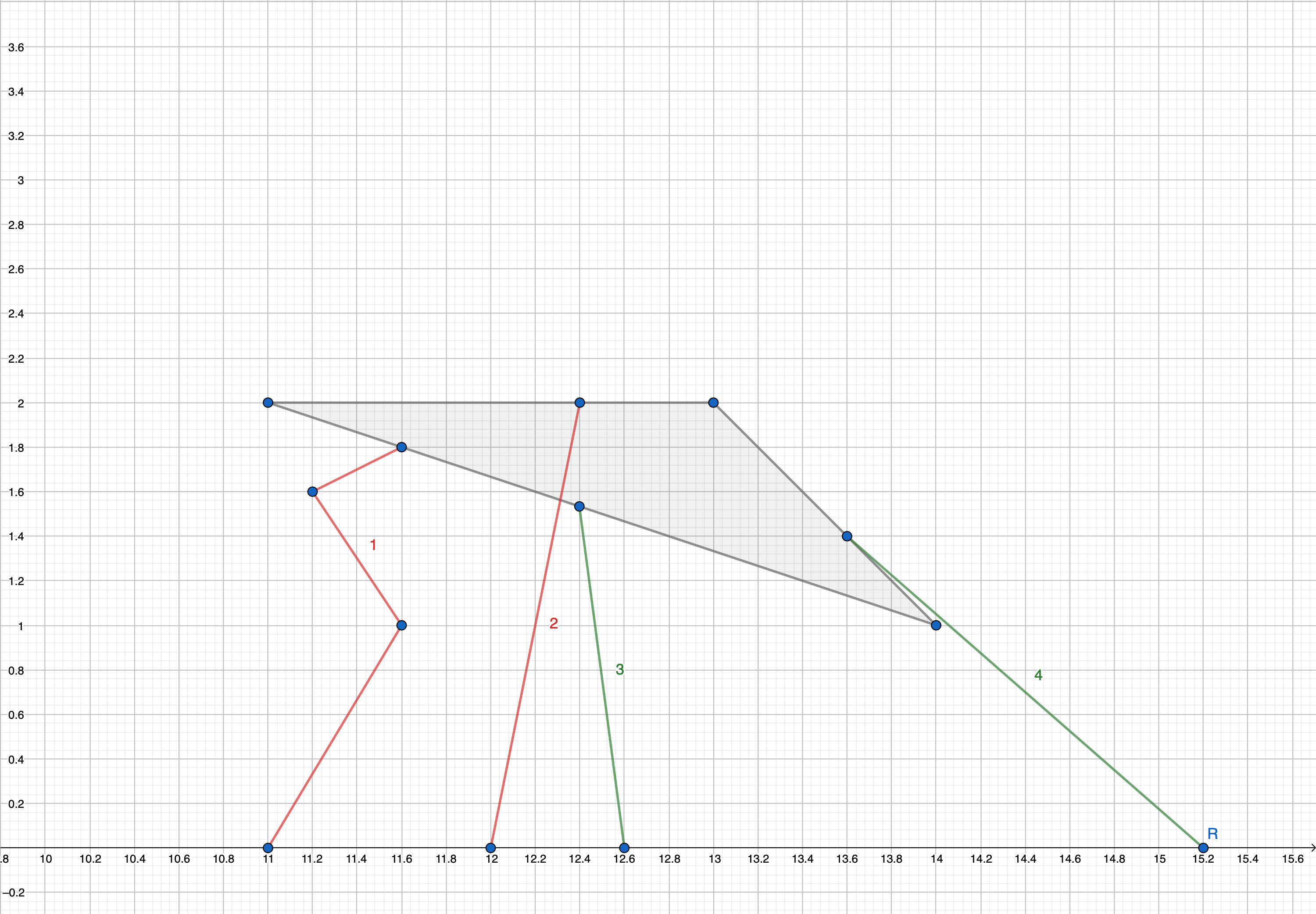
比如这个样例。

第一条线是不满足题意的，因为它不是直线。

第二条线也是不满足题意的，但是它穿过了这个三角形的内部，

第三条线和第四条线都是满足题意的，这两个连接的点也都是安全的。

解题

可以把这个三角形分为三条线段，对每一条线段思考。

用解析式表示一条线段，可以发现如果这个一次函数不是一个常函数，在数轴上一定可以找到一个点连接到这条线段而不经过三角形的内部。

若延长这条线段，与数轴的交点以右的所有点都可以满足题意。

反之，如果这条线段是一个常函数，与数轴就没有交点，就是不满足题意的点。

本题就转换为了一个求和 \(x\) 轴平行的线的长度。

模拟一下就可以了。

/*
Writer:ZhengXiangYu
*/
#include <bits/stdc++.h>
#define IOS std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0)
#define fre(a) freopen(#a".in", "r", stdin), freopen(#a".out", "w", stdout)

using i64 = long long;
constexpr i64 eps = 1e-9;
constexpr i64 N = 5;
 
struct node {
  i64 x, y;
} a[N + 1];
int main() {
  IOS;
  
  i64 T;
  std::cin >> T;
  while (T--) {
  	for (i64 i = 1; i <= 3; i++) {
	  std::cin >> a[i].x >> a[i].y;
	}
	i64 p = -1, q = -1, s = -1;
	for (i64 i = 1; i <= 3; i++) {
	  for (i64 j = i + 1; j <= 3; j++) {
		if (a[i].y == a[j].y && a[i].y && a[j].y) {
		  q = i, p = j, s = 6 - i - j;
		  break;
		}  
	  }
	}
//	std::cout << p << " " << q << " " << s << "\n";
	if (p == -1 || q == -1) {
	  std::cout << 0 << "\n";
	} else {
	  if (a[s].y <= a[p].y) {
	  	std::cout << abs(a[p].x - a[q].x) << "\n";
	  } else {
	  	std::cout << 0 << "\n";
	  }
	}
  }
  return 0;
}