特征分析

描述

本文归纳数据清洗后到建模前的工作内容。随着阅读量和工作经验的增加慢慢扩充积累

在数据清洗结束后，要着手分析各项特征，进行筛选建模。特征的分析和筛选是建模工作中最繁杂、工作量最高的环节。
在sklearn的apifeature_selection中有很多通识方法，此外在部分模型如随机森林中集成有rf.feature_importances_来给出各个特征的重要性排名。这种自含的方法在个人快速建模时非常实用，但在需要进行业务解释的场景时集成度过高无法拆解和说服业务人员。本文尝试结合人工变量分析筛选依据和业界标准理论的分析筛选方案记录。
博文中如果理解有误请大佬斧正，在下必定垂耳倾听。

特征分析流程

1.有效值分析

在实际问题中，很多数据特征项无法获取或者极度不均衡。例如“未知”占比达到99%，或者“否”占比高于95%。这样的特征违背了显著性检验的思想，是需要剔除的。
关于显著性检验的理解，请看此文章：知乎假设检验P值含义马同学回答

1.1众数占比过滤

计算各项特征众数占比R_mode，过滤掉大于0.95的特征。

1.2方差过滤

方差（Variance）表示一组数据的波动性。计算各个特征数据的方差,逆序排序。
除了可以直接计算方差的数值型特征外，还有字符类型的离散特征。此时可用使用pandas的pd.factorize进行数值编码。

数值型的特征和离散型的特征的方差不在一个维度之上，因此区分能力不会太好。作为一种快速理解数据的操作，需要甄别以后自行判断特征有效性是否达到要求。

2.特征筛选

特征筛选是依据评估指标过滤筛选出对模型目标结果影响较高的特征。sklearn的feature_selection.SelectKBest可以按指定的评估方法输出各个特征的重要性。
特征规约指从互相关的角度对数据进行降维。
特征筛选和特征规约，两种操作都是对特征数做减法，二者的先后顺序可以视情况而定。推荐先做比较容易的特征筛选，后做特征规约。

2.1特征筛选

在不同的机器学习模型中，有不同的常用特征评估方法。这部分列举一些筛选用的指标。

2.1.1 IV（information value）值

在逻辑回归模型中，IV值是常用的特征评估方法。iv值和逻辑回归模型广泛应用在银行的评分卡模型中。
（在银行征信评估中，建模评估目标是失信分数，目标样本通常是y=0的样本。而本人项目经验是建立用户价值评分模型，目标样本是y=1的样本。因此在建模过程的正负取值、正负样本的描述上需要与其他评分卡模型文章相甄别）

在IV之前，需要了解证据权重WOE(weight of evidence)

WOE值计算

woe针对一个特征的一种取值。例如有个特征是否获奖的取值范围是{True,False},那么该特征的True和False取值各对应一个woe值。
woe计算方法：

1.总体正样本数tg
2.总体负样本数tb
3.该特征取值的正样本数p
4.该特征取值的负样本数n
5.该特征正样本数在全体正样本占比\(pr=\frac{p}{tg}\)
6.该特征负样本数在全体负样本占比\(nr=\frac{n}{tb}\)
5.计算\(woe=In(\frac{pr}{nr})\)

IV值计算

IV值针对的是一个特征，由该特征各个取值的woe值计算而来。

\[IV=\sum_{i=1}^m (pr_i-nr_i)*woe_i \]

IV值指示了该特征对建模目标结果的区分度。IV值越高表示该特征不同取值对y变量的区分度越明显。一般IV值大于0.02即可选择该特征参与建模。IV值大于0.5则考虑该将该特征作为规则处理。

下面是本人的一点见解：
Q₁：为什么需要对特征进行woe编码？
A₁：可以看到计算woe时，特征都是离散型的变量。当特征是连续型的数值时，需要先分箱处理，将连续型的数值划分到多个区间（分箱方法使用pd.cut和pd.qcut，分箱、合并有很多内容请自行研究），转换成离散型变量。在连续型变量分箱转换为woe编码时，天然地克服了离群异常值和缺失值的问题，且允许特征取值有微小波动时含义不变，使特征的稳定性增强。
此外，逻辑回归的原理是用多项式的sigmoid函数拟合因变量y。

\[y=\frac{1}{1+e^{-(WX+b)}} \]

经过变形得到

\[In(\frac{y}{1-y})=WX+b\tag{1} \]

而woe编码将数值特征转化为不同区间段内正样本率的对数变换：

\[woe=In(\frac{pr}{nr})\\ =In(\frac{p}{tg}/\frac{n}{tb})\\ =In(\frac{p}{n}*\frac{tb}{tg})\\ =In(\frac{p}{n})+Const \tag{2} \]

而该区间正样本率\(p_i=\frac{p}{n+p}\).将\(p_i\)代入(2)中，得到：

\[woe=In(\frac{p}{n})+Const\\ =In(\frac{n+p}{n}-1)+Const\\ =In(\frac{p_i}{1-p_i})+Const \]

而woe替换成x后代入(1)中进行拟合。会发现多项式拟合目标\(In(\frac{y}{1-y})\)和woe编码后的自变量x：\(In(\frac{p_i}{1-p_i})\)形态一致！。说明woe编码将自变量投射到因变量的线性空间中。woe编码和逻辑回归模型在数学上达到了完美的契合。这就是woe编码在逻辑回归评分卡模型中不可替代的原因。
Q₂:如何理解模型的输入输出？
A₂:自变量-->分箱映射成类别-->计算该类别的woe值-->作为逻辑回归模型的自变量x_i-->通过训练出的系数(lr.coef_)和常数项(lr.intercept_)计算得到标签(lr.predict)或者sigmoid概率y(lr.predict_proba)

3.相关性分析

相关性分析既适用于特征-因变量间做特征的挑选，又适用于特征-特征间去掉共线性强的特征组合。在实际的工作中，特征与特征的关系可能很紧密，有的特征是前面一个特征直接映射加工得来的。

如何理解相关性？

这里引用《数据挖掘导论》的关于相异性和相似性的部分内容以及自己的理解。

用术语邻近度proximity表示相似性或相异性。通过两个对象对应属性之间的邻近度函数计算。

相异度(dismilarity)和相似度(similarity)是互为1的补数关系，二者是可以转化的。而相异度与距离(distance)是同义词。
相异度概念的源头就是距离，从一维到多维，从直白的运算到加权和规范化。

例如我们熟知的两个点间的欧氏距离：\(d(x,y)=\sqrt{\sum_{k=1}^n (x_k-y_k)^2} \quad\)

欧氏距离的推广式闵可夫斯基距离(Minkowski distance)：

\[d(x,y)=(\sum_{k=1}^n |x_k-y_k|^r)^{1/r} \]

• r=1,表示曼哈顿距离，L1范式
• r=2,表示欧几里得距离，L2范式
• r=\(\infty\)，上确界距离。

除了距离，相似度和相异度在特殊的对象间有特殊的度量方式。
例如：

• 简单匹配系数(Simple Matching Coefficient,SMC)
• Jaccard系数
  上述两个系数仅用在处理二元属性的对象间。而Jaccard系数是SMC在非对称数据集的改良。
• 余弦相似度

\[cos(x,y)=\frac{x·y}{||x||||y||} \]

余弦相似度是个高度抽象的相似性度量。它代表了矢量间的通用的相似性。Pearson系数就是其"精神续作"。

3.1 相关系数

1. Pearson相关系数
2. Spearman相关系数
3. kendall相关系数

相关系数可以通过pandas的df.corr来计算。通常是直接计算Pearson相关系数。
Pearson相关系数的理解推荐这个回答：如何理解皮尔逊相关系数（Pearson Correlation Coefficient）？
但Pearson相关系数有局限性，无法计算连续型序列和离散型序列的相关系数。Spearman系数则可以计算任意类型特征的相关系数。
kendall相关系数尚未研究过。

通过相关系数可以排序、过滤筛选特征对因变量的贡献，从而筛选变量。

3.2 卡方独立性检验

卡方检验适用于分类序列间的相关性检测。
卡方检验是从统计学、假设检验的角度去论证序列的相关性，是不同于“距离”核心概念的度量。依赖于概率模型，相关性的计算直接来源于样本的分布。
卡方检验是一种非参检验。非参检验不存在具体参数和总体正态分布的假设，所以有时被称为自由分布检验。

参数和非参数检验最明显的区别是它们使用数据的类型。

非参检验通常将被试分类，如民主党和共和党，这些分类涉及名义量表或顺序量表，无法计算平均数和方差。

这里说一下个人见解：在一个模型中，特征有连续的数值型特征例如收入，也有类别特征例如性别。在处理连续型特征时，特征可四则运算，可以使用纯代数方式进行最小二乘法回归分析。而在处理类别特征时，序列不存在“均值”、“方差”等数学概念，只能从概率的角度出发，分析类别的分布，比如这里提到的卡方检验相关性以及上文中提到的证据权重woe。

那么在卡方独立性检验中，算出的p值该怎么理解呢？

独立性检验的原假设是：两个序列独立

p值表示原假设成立的概率，当p<0.05时，我们拒绝原假设。即两个序列不独立。

在建模过程中，可以使用卡方独立性检验筛选特征，计算每个特征和因变量的p值，也可以计算特征互相间的p值。使用sklearn.feature_selection.chi2进行卡方检验。原则是，特征与因变量相关，即p值越小越好；特征与特征间独立，p值越大越好。

3.3 互信息(Mutual Information)和最大信息系数(Maximal Information Coeffient)

这个相关性检验的方法还没实际使用过。这里附上万维百科的Maximal Information Coeffient词条链接。
在参考文章1中有简单的介绍和与SelectKBestAPI联动的例子。

这里总结一下我在万维百科里捕捉到的几条结论：

1. In statistics, the maximal information coefficient (MIC) is a measure of the strength of the linear or non-linear association between two variables X and Y.
   简单翻译：MIC是指示两个变量X和Y之间线性和非线性强度的度量
2. MIC outperformed some selected low power tests, however concerns have been raised regarding reduced statistical power in detecting some associations in settings with low sample size when compared to powerful methods such as distance correlation and Heller–Heller–Gorfine (HHG)
   简单翻译：在低功效检验（参考文章：检验功效（Power）与样本量）中表现优异。但是处理小数据集是效果不如距离相关性和HHG
3. The maximal information coefficient uses binning as a means to apply mutual information on continuous random variables.
   简单翻译：最大信息系数通过分箱的方法对连续随机变量应用互信息。（也就是说MIC还是一种计算分类变量相关性的方法）
4. what MIC contributes in addition is a methodology for selecting the number of bins and picking a maximum over many possible grids.
   简单翻译：MIC可以应用在选定最佳分箱数和在许多可能的网格中挑选最大值（后半截我也不明白）

3.4 距离相关系数(distance correlation)

这里先附上万维百科的距离相关系数连接

重要结论是，距离相关系数可以检验变量间的线性和非线性相关性。而Pearson系数只能检验两者的线性相关性。

3.5 HHG

这里引用文章:统计学：HHG相关性算法

3.6 VIF(Variance-Inflation-Factor)

VIF（方差膨胀检验）方法，可对因子之间的线性相关关系进行检验，从而帮助选取到独立性更好的因子，增强因子模型的解释能力。

在线性回归方法里，应用最广泛的就是最小二乘法（OLS），只不过我们对每个因子，用其他Ｎ个因子进行回归解释。

注：之所以不使用协方差计算相关性是由于协方差难以应用在多元线性相关情况下。给出VIF计算方法：

\[VIF=\frac{1}{1-R^2} \]

其中有一个检验模型解释能力的检验统计指标为\(R^2\)（样本可决系数），\(R^2\)的大小决定了解释变量对因变量的解释能力。而为了检验因子之间的线性相关关系，我们可以通过OLS对单一因子和解释因子进行回归，然后如果其\(R^2\)较小，说明此因子被其他因子解释程度较低，线性相关程度较低。很容易看出，VIF越高解释变量和因变量之间线性相关性就越强。

VIF通过回归模型计算，但是任然是挑选特征的先验方法。

4.特征规约

即特征降维。前面提到的概念是衡量序列间相关性的指标，设定阈值后，解决变量挑选的问题。这里的几个概念使用矩阵分解的方法发掘和处理变量-变量间的相关性问题。

除了直接计算变量间的互相关性，在高相关性的变量组中择优录取。类似L1正则化。
还可以选择使用PCA和LDA降维，将高相关性的变量间映射变换成一个新的变量。

4.1 奇异值分解SVD

4.2 主成分分析PCA

推荐两篇文章：
如何通俗易懂地讲解什么是 PCA（主成分分析）
如何通俗易懂地讲解什么是 PCA（主成分分析）- 武辰

总结一下就是一组特征通过互相的坐标变换，将方差较小的特征投射到新的正交基上，并用新的正交基表示留下的特征。
PCA不局限于一对一的降维，可以对所有特征进行变换，然后人为选择前N大的奇异值数量维度的特征。

关于PCA和SVD，这里引用一个很好地总结,来源于知乎文章评论区用户刘思黎的回答：

试着解释一下SVD矩阵：在我看来，SVD是对数据进行有效特征整理的过程。首先，对于一个m×n矩阵A，我们可以理解为其有m个数据，n个特征，（想象成一个n个特征组成的坐标系中的m个点），然而一般情况下，这n个特征并不是正交的，也就是说这n个特征并不能归纳这个数据集的特征。SVD的作用就相当于是一个坐标系变换的过程，从一个不标准的n维坐标系，转换为一个标准的k维坐标系，并且使这个数据集中的点，到这个新坐标系的欧式距离为最小值（也就是这些点在这个新坐标系中的投影方差最大化），其实就是一个最小二乘的过程。进一步，如何使数据在新坐标系中的投影最大化呢，那么我们就需要让这个新坐标系中的基尽可能的不相关，我们可以用协方差来衡量这种相关性。A^T·A中计算的便是n×n的协方差矩阵，每一个值代表着原来的n个特征之间的相关性。当对这个协方差矩阵进行特征分解之后，我们可以得到奇异值和右奇异矩阵，而这个右奇异矩阵则是一个新的坐标系，奇异值则对应这个新坐标系中每个基对于整体数据的影响大小，我们这时便可以提取奇异值最大的k个基，作为新的坐标，这便是PCA的原理。

4.3 线性判别分析LDA(Linear Discriminant Analysis)

参见这篇文章：线性判别分析（LDA）

LDA的思想是将一个高维空间中的数据投影到一个较低维的空间中，且投影后要保证各个类别的类内方差小而类间均值差别大，这意味着同一类的高维数据投影到低维空间后相同类别的聚在一起，而不同类别之间相距较远。在图像识别等模式识别领域运用非常广泛。

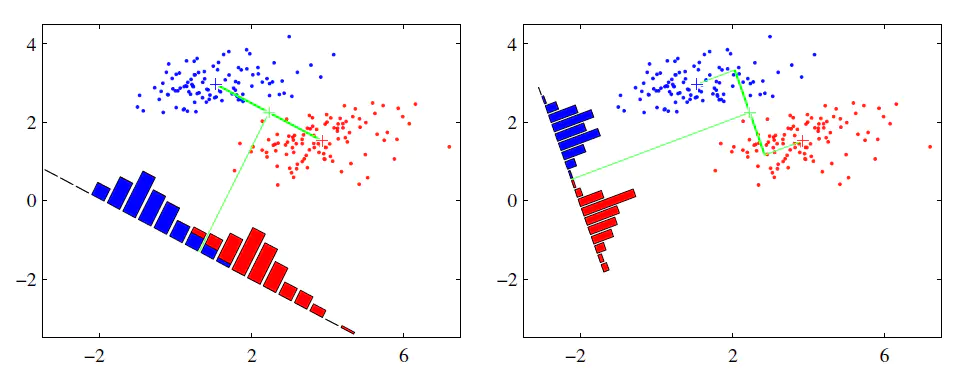
图中通过LDA将二维平面上的点投影到直线上，两个特征降成一维。

可以发现LDA是以分类标签做依据进行的有监督降维，它的使用流程通PCA比起来，类似于后验（LDA通过分类结果去推断降维方法，果-->因。再以得到的降维方法去处理待遇测的样本）和先验（PCA不必事先知道样本类别，仅通过两特征序列间的相关性进行维度压缩）的区别。

集成的特征筛选方法

业界将特征挑选的方法分为三个大类别。这三大思想的运用比较成熟，在现有的机器学习库中已具有相关的API。

1.过滤法Filter

按照发散性或相关性对各个特征进行评分，设定阈值或者待选择特征的个数进行筛选。

基本想法是：分别对每个特征\(x_i\)，计算\(x_i\)相对于类别标签\(y\)的信息量\(S(i)\)，得到\(n\)个结果。然后将\(n\)个\(S(i)\)按照从大到小排序，输出前\(k\)个特征。显然，这样复杂度大大降低。那么关键的问题就是使用什么样的方法来度量\(S(i)\)，我们的目标是选取与\(y\)关联最密切的一些特征\(x_i\)。

例如：

• Pearson相关系数
• 卡方验证
• 互信息和最大信息系数
• 距离相关系数
• 方差选择法
  等上一节中介绍的诸多特征度量。

过滤法通过sklearn.feature_selection.SelectKBest实现。
这个文章对该API讲解很细致：每天一点sklearn函数之SelectKBest（9.5）
还阔以看官方文档：https://scikit-learn.org/stable/modules/generated/sklearn.feature_selection.SelectKBest.html

这里测试了一下SelectKBest的k取all时候的功能。

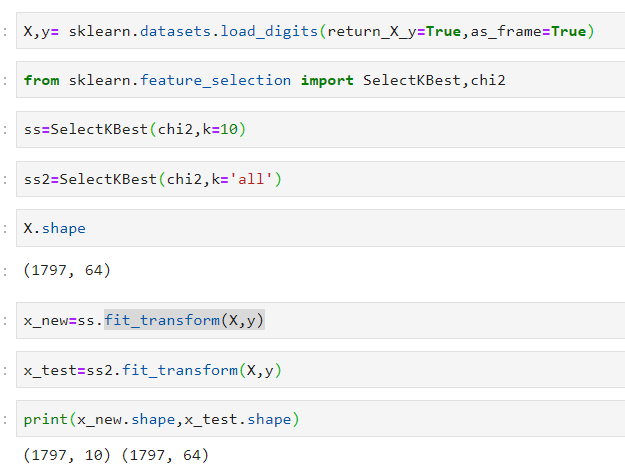
结果是没什么用，k='all'时表示不进行变量的挑选。

总结一下：过滤法，关键的两个参数：score评价函数和保留特征数k。依据score函数对所有特征进行评分，按得分排序书输出制定的k个特征。有趣的问题是，如果一个评价函数的结果和特征是负相关，及函数结果越大，特征贡献度越小。那么这个SelectKBest还是需要做一点手动的调整，可以把得分函数修饰一下，乘以负一。

2.包装法Wrapper

根据目标函数（往往是预测效果评分），每次选择若干特征，或者排除若干特征

基本思想：基于hold-out方法，对于每一个待选的特征子集，都在训练集上训练一遍模型，然后在测试集上根据误差大小选择出特征子集。需要先选定特定算法，通常选用普遍效果较好的算法， 例如Random Forest， SVM， kNN等等。

贪婪搜索算法（greedy search）是局部最优算法。与之对应的是穷举算法 (exhaustive search)，穷举算法是遍历所有可能的组合达到全局最优级，但是计算复杂度是2^n，特征数量和数据量较大时是不太实际的算法。

2.1 前向搜索

前向搜索说白了就是，每次增量地从剩余未选中的特征选出一个加入特征集中，待达到阈值或者 n 时，从所有的 F 中选出错误率最小的。

2.2 后向搜索

既然有增量加，那么也会有增量减，后者称为后向搜索。先将 F 设置为 {1,2,...,n} ，然后每次删除一个特征，并评价，直到达到阈值或者为空，然后选择最佳的 F 。

2.3 递归特征消除法

反复创建模型，并在每次迭代时保留最佳特征或是剔除最差特征，下一次迭代时，它会使用上一次建模中没有被选中特征来构建下一个模型，直到所有的特征都耗尽为止。然后，它根据子集保留或是剔除特征的顺序来对特征进行排名，最后选出一个最佳子集。包装法的效果是所有特征选择方法中最利于提升模型表现的，它可以使用很少的特征达到很优秀的效果。

递归训练消除法的在sklearn中有对应API：sklearn.feature_selection.RFE
RFE有两个重要的参数：选择的模型estimator和需要保留的特征数量n_features_to_select，其原理是使用一个基模型来进行多轮训练，每轮训练后通过学习器返回的 coef_ 或者feature_importances_ ，依据其系数大小排序，消除若干权重较低的特征，再基于新的特征集进行下一轮训练。

包装法选取特征的操作是直白暴力的，递归地选取特征组合，因此需要的计算成本是最高的。

3.嵌入法Embedded

先使用某些机器学习的模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征（类似于Filter，只不过系数是通过训练得来的）。

在形态上和过滤法有些一脉相承。区别在于，过滤法是计算各个特征评估函数的结果择优录取，而嵌入法则是通过全体特征进行模型训练，在各个特征得到的系数中择优录取。分别对应先验和后验的思想。

在sklearn中api如下sklearn.feature_selection.SelectFromModel。
有两个重要参数：阈值threshold和max_features.分别表示通过权重的数值门限选择和排序选择。

其他

LASSO(least absolute shrinkage and selection operator，最小绝对值收缩和选择算子)

可以解决特征的共线性问题，L1正则化将共线性强且对建模贡献度低的特征系数置为0，从而达到筛选特征的目的。

在sklearn中有APIsklearn.linear_model.Lasso

有一个令人感动的positive参数，强制系数为正。当初算相关系数，手动查看如何组合调整才能保证系数为正。
特别说明当惩罚项alpha=0时，lasso作用和linearRegression模型通化。这说明什么呢，说明LASSO的原理还是和线性回归一样的最小二乘法（目标是误差均方差最小的方程组系数求解）。当alpha=0时效果应当和LR的L2正则化效果相同。

参考文章

1.【机器学习】逻辑回归（非常详细）
2.Softmax函数和Sigmoid函数的区别与联系
3.卡方检验（Chi-Squared Test）
4.Maximal Information Coeffient
5.距离相关系数
6.检验功效（Power）与样本量
7.VIF方法（方差膨胀因子）因子独立性检验 全流程解读
8.统计学：HHG相关性算法
9.如何通俗易懂地讲解什么是 PCA（主成分分析）？ - 武辰
10.特征选择的包装法Wrapper