霍夫线变换
霍夫线变换
原理
Note
以下原理的说明来自书籍 学习OpenCV 作者Bradski和Kaehler.
霍夫线变换
- 霍夫线变换是一种用来寻找直线的方法.
- 是用霍夫线变换之前, 首先要对图像进行边缘检测的处理,也即霍夫线变换的直接输入只能是边缘二值图像.
它是如何实现的?
-
众所周知, 一条直线在图像二维空间可由两个变量表示. 例如:
- 在 笛卡尔坐标系: 可由参数:
![(m,b)]() 斜率和截距表示.
斜率和截距表示. - 在 极坐标系: 可由参数:
![(r,\theta)]() 极径和极角表示
极径和极角表示
![Line variables]()
对于霍夫变换, 我们将用 极坐标系 来表示直线. 因此, 直线的表达式可为:
![y = \left ( -\dfrac{\cos \theta}{\sin \theta} \right ) x + \left ( \dfrac{r}{\sin \theta} \right )]()
化简得:
![r = x \cos \theta + y \sin \theta]()
- 在 笛卡尔坐标系: 可由参数:
-
一般来说对于点
![(x_{0}, y_{0})]() , 我们可以将通过这个点的一族直线统一定义为:
, 我们可以将通过这个点的一族直线统一定义为:![r_{\theta} = x_{0} \cdot \cos \theta + y_{0} \cdot \sin \theta]()
这就意味着每一对
![(r_{\theta},\theta)]() 代表一条通过点
代表一条通过点 ![(x_{0}, y_{0})]() 的直线.
的直线. -
如果对于一个给定点
![(x_{0}, y_{0})]() 我们在极坐标对极径极角平面绘出所有通过它的直线, 将得到一条正弦曲线. 例如, 对于给定点
我们在极坐标对极径极角平面绘出所有通过它的直线, 将得到一条正弦曲线. 例如, 对于给定点 ![x_{0} = 8]() and
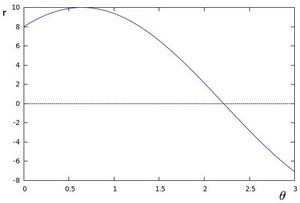
and ![y_{0} = 6]() 我们可以绘出下图
(在平面
我们可以绘出下图
(在平面 ![\theta]() -
- ![r]() ):
):![Polar plot of a the family of lines of a point]()
只绘出满足下列条件的点
![r > 0]() and
and ![0< \theta < 2 \pi]() .
. -
我们可以对图像中所有的点进行上述操作. 如果两个不同点进行上述操作后得到的曲线在平面
![\theta]() -
- ![r]() 相交,
这就意味着它们通过同一条直线. 例如, 接上面的例子我们继续对点:
相交,
这就意味着它们通过同一条直线. 例如, 接上面的例子我们继续对点: ![x_{1} = 9]() ,
, ![y_{1} = 4]() 和点
和点 ![x_{2} = 12]() ,
, ![y_{2} = 3]() 绘图,
得到下图:
绘图,
得到下图:![Polar plot of the family of lines for three points]()
这三条曲线在
![\theta]() -
- ![r]() 平面相交于点
平面相交于点 ![(0.925, 9.6)]() ,
坐标表示的是参数对 (
,
坐标表示的是参数对 (![\theta, r]() ) 或者是说点
) 或者是说点 ![(x_{0}, y_{0})]() ,
点
,
点 ![(x_{1}, y_{1})]() 和点
和点 ![(x_{2}, y_{2})]() 组成的平面内的的直线.
组成的平面内的的直线. -
那么以上的材料要说明什么呢? 这意味着一般来说, 一条直线能够通过在平面
![\theta]() -
- ![r]() 寻找交于一点的曲线数量来 检测.
越多曲线交于一点也就意味着这个交点表示的直线由更多的点组成. 一般来说我们可以通过设置直线上点的 阈值 来定义多少条曲线交于一点我们才认为 检测 到了一条直线.
寻找交于一点的曲线数量来 检测.
越多曲线交于一点也就意味着这个交点表示的直线由更多的点组成. 一般来说我们可以通过设置直线上点的 阈值 来定义多少条曲线交于一点我们才认为 检测 到了一条直线. -
这就是霍夫线变换要做的. 它追踪图像中每个点对应曲线间的交点. 如果交于一点的曲线的数量超过了 阈值, 那么可以认为这个交点所代表的参数对
![(\theta, r_{\theta})]() 在原图像中为一条直线.
在原图像中为一条直线.
标准霍夫线变换和统计概率霍夫线变换
OpenCV实现了以下两种霍夫线变换:
- 标准霍夫线变换
- 原理在上面的部分已经说明了. 它能给我们提供一组参数对
的集合来表示检测到的直线
- 在OpenCV 中通过函数 HoughLines 来实现
- 统计概率霍夫线变换
- 这是执行起来效率更高的霍夫线变换. 它输出检测到的直线的端点
- 在OpenCV 中它通过函数 HoughLinesP 来实现
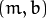 斜率和截距表示.
斜率和截距表示.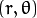 极径和极角表示
极径和极角表示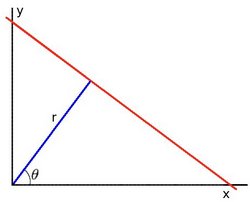
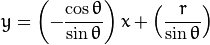
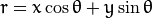
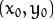 , 我们可以将通过这个点的一族直线统一定义为:
, 我们可以将通过这个点的一族直线统一定义为: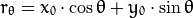
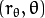 代表一条通过点
代表一条通过点 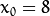 and
and 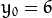 我们可以绘出下图
(在平面
我们可以绘出下图
(在平面 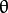 -
- 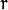 ):
):
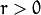 and
and 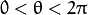 .
.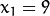 ,
, 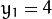 和点
和点 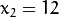 ,
, 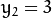 绘图,
得到下图:
绘图,
得到下图: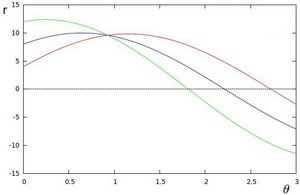
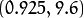 ,
坐标表示的是参数对 (
,
坐标表示的是参数对 (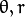 ) 或者是说点
) 或者是说点 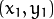 和点
和点 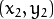 组成的平面内的的直线.
组成的平面内的的直线.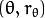 在原图像中为一条直线.
在原图像中为一条直线.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号