递归应用->快速排序算法

简单总结：分而治之，然后递归

1.取一个基准值对所有待排序元素分区。 比基准值小的元素放左边，比基准值大的元素放右边

     基准值最好是随机选出来的，尽可能避免最坏情况，可参考《剑指Offer 数据结构与算法名企面试题精讲》（何海涛著）第12.3章节，代码虽然麻烦点，但是效率得到了保障，如果读者不理解如何对数组快速排序，也可参阅此章节。

     本例选第一个元素作为基准值，不是最优解，但是代码量少，适合笔试用。

2. 分别对左边元素 和 右边元素执行上述步骤，直到待排序元素个数<=1, 跳出递归

快速排序平均运行时间为O(nlogn)，最糟情况的运行时间为O(n平方)，详情可参阅《算法图解》（Aditya Bhargava著 袁国忠译）第4.3章节

package xia.test;

import java.util.Arrays;

public class Digui {
  
    public void quickSort(int[] a, int begin, int end){
        //递归的基线条件：如果待排序的数组元素只有一个或没有时（end-begin<1），不用排序，退出递归
        if(end-begin<1){
            return ;
        }
        //递归条件：数组元素>1个

        //设置基准值(取begin位置的元素值)
        int base = a[begin];

        //对数组索引为begin和end之间的区域进行分区，使小于等于基准值的元素处于基准值的左侧，大者处于基准值的右侧
        //分区开始
        //用两个指针，left和right
        int left = begin;
        int right = end;
        while (left < right){
            //1. right从end出发往左，找到第一个比基准值小的元素
            while(a[right]>base && left<right){
                right--;
            }
            //2. left从begin出发往右，找到第一个比基准值大的元素
            while(a[left]<=base && left<right){
                left++;
            }

            //3. 如果left与right没有相逢，交换left与right的元素
            if(left!=right){
                int temp = a[left];
                a[left] = a[right];
                a[right] = temp;
            }

            //4. left继续往右走，right继续往左走，重复1-4步
        }

        //如果left与right相逢，即表示begin与end区域内的元素都遍历完了，碰撞点左侧都是小于或等于基准值的元素，右侧反之。
        //此时基准值还在begin位置，应将它移到碰撞点（交换begin和left的元素）
        a[begin] = a[left];
        a[left] = base;
        //分区结束

        //递归调用本方法，对基准值左侧的数组进行排序
        quickSort(a, begin, left-1);

        //递归调用本方法，对基准值右侧的数组进行排序
        quickSort(a, left+1, end);
    }


    public static void main(String[] args) {
        Digui digui = new Digui();
        int[] b = {3,2,1,5,4,8, 6};
        digui.quickSort(b, 0, 6);
        System.out.println(Arrays.toString(b));
    }
}

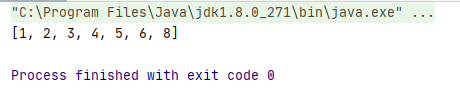
运行结果：