今天的算法课是学习在线算法，在计算机科学中，一个在线算法是指它可以以序列化的方式一个个的处理输入，也就是说在开始时并不需要已经知道所有的输入。相对的，对于一个离线算法，在开始时就需要知道问题的所有输入数据，而且在解决一个问题后就要立即输出结果。例如，选择排序在排序前就需要知道所有待排序元素，然而插入排序就不必。
举的例子有：1.沿城墙走找门。2.发扑克牌，最大点数。3.选择item.
听到的重点是：1. Competitiveness的概念。2. 老师反复提到的adversary。
Competitiveness，简单来说就是我们设计的算法的收益，代价什么的和最优算法的比值，用这个来衡量我们算法的好坏。对于最优算法OPT，我们并不知道它具体是什么，只知道有这么个算法能得到最优结果。对于如何考虑离线算法，因为不知道全局的情况。 可以考虑有一个敌人(adversary)，总是让我们的算法陷入最坏的情况，让我们达不到好的Competitiveness，下面以例子说明。
例子1：一座城墙，有一个城门，初始你在城墙的某个地方，你想到城门那，在你左边或者右边，你不知道城墙的具体位置，方向。这个时候如何走才能使你找到城墙的时候走的距离最小呢？
因为不知道全局情况是什么，所以这里想要设计出比较好的算法比较困难，所以，对于离线算法，首先考虑的是最优算法OPT是什么，再来看看它会怎么“整“你。对于最优算法来说，因为它是知道全局情况的，所以对于他来说直接走到门那里就ok了，假设初始位置离城门的位置是y，那么最优算法OPT走的距离就是y。最优算法我们知道了，现在想的是有个adversary会怎么使我们的算法更坏，使我们的算法走多少个y呢？
假设我现在定的算法是朝着某一方向，加入是左边走x距离，如果没找到门则折回并往反方向右走2x距离，再没找到就再折回，往反方向走上一个距离的2倍。如果是这样的算法的话，那么这个adversary会怎么整我们呢？它可能会将城门的位置设置在x+ε（ε很小）或者设置在与我们走的初始位置反方向的2x+ε处(这里开始我有疑问，为什么不把城门的位置设大点好让我们的算法对此来回走，后来用笔计算了下，这样我们的最优算法OPT也会变大，ALG/OPT的结果反而变小，这不是adversary所希望的)。那么Competitiveness的情况如下：
即Competitiveness的最优值会接近8，就是说最多会走最优解的8倍距离。老师也说了，可以将往回走的值设为3倍及以上也可，计算出来的结果表明取2倍的距离会得到最好的Competitiveness。
例子2：发扑克牌问题，大致意思(我没听错的话)就是adversary从一副扑克牌中依次选10张牌，每次选出一张给你要还是不要，你只能要一张。对于最优算法OPT来说，因为它知道全局情况他可以任意依次选10张牌，但是他的目的是使你的Competitiveness尽可能不利，即这里的adversary的目标是使你选较小的牌，而最优算法会选较大的牌从而使Competitiveness变大(OPT/ALG)，那么它的策略是在前九张不会放较大的数字，比如说一直放4，你可能犹豫不觉，到了倒数第二张，如果你选了4，那么adversary就放13(k)。如果你不选4，那么最后一张就放1，这两种情况下的Competitiveness分别为13/4和4/1.
这样总结的到的结论是：对于在线算法，因为没办法知道全局情况(事先的全部输入),所以不可能好过最优算法，我们要考虑的是最坏的情况下怎么取得较好的Competitiveness
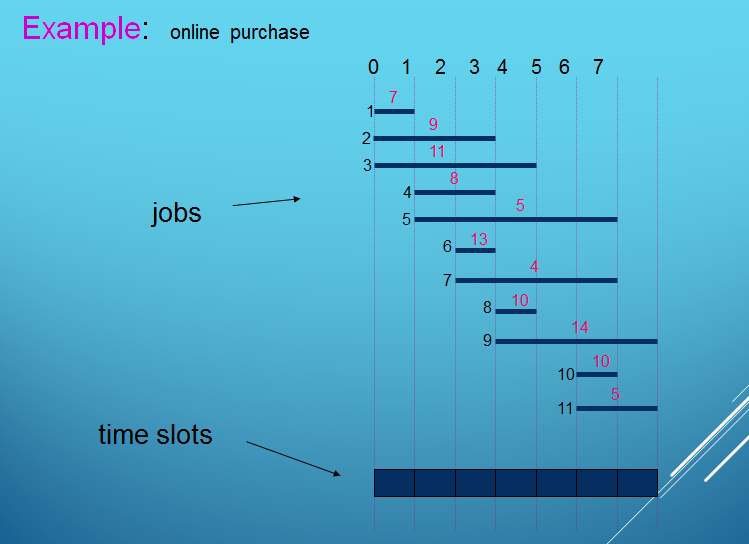
例3：工作调度问题(据说是谷歌的面试题)，题目的意思我好想理解的有问题。。。。。。，这里暂且不分析了，以后自己搞明白了再回来写
