基环树
具有环的树
两种抽象理解的方式
1.一个环,环上每一个点都是一棵树的根节点
岛屿(AcWing358)
求基环森林的各棵基环树的直径总和
直径分两种情况:
1.不在环上,在环中某节点子树内
2.经过环上两点x,y,并延伸至x,y的子树,\(len=dis(x,y)+f[x]+f[y]\)
枚举每个点,如果没有被访问过,遍历它所在的基环树,进行计算
两种找环方式:
1.dfn序(常见方式)
int dfn[N],idd;
struct aaa{
int x,w;
}fa[N];
void dfs(int x)
{
dfn[x]=++idd;
for(int i=hd[x];i;i=nx[i])
{
if(dfn[to[i]])
{
if(dfn[to[i]] < dfn[x]) continue;//他的父节点
lop[++c]=to[i],dis[c]=d[i],b[to[i]]=1;
for(int y=to[i];y!=x;y=fa[y].x)//记录环
lop[++c]=fa[y].x,dis[c]=fa[y].w,b[fa[y].x]=1;
}
else
{
fa[to[i]].x=x,fa[to[i]].w=d[i];//记录从哪来的
dfs(to[i]);
}
}
}
2.找到直接返回型(需要在找子树直径时补全ck数组!! )
int dfs(int x,int ii)
{
if(ck[x])
{
rt=x;
return 1;
}
ck[x]=1;
int fg;
for(int i=hd[x];i;i=nx[i])
{
if(i==ii) continue;
fg=dfs(to[i],i^1);
if(fg)
{
if(fg==1)
{
lop[++c]=x,dis[c]=d[i],b[x]=1;
if(rt!=x) return 1;
}
return 2;
}
}
return 0;
}
树形dp:处理子树的最长路径(顺便求树内直径)
void sol(int x,int fa)
{
ck[x]=1;//dfs(x,ii) 只能找到环,并不能遍历该树内所有点,有的ck[x]没被设成1
for(int i=hd[x];i;i=nx[i])
{
if(to[i]==fa||b[to[i]]/*不能往环上整*/) continue;
sol(to[i],x);
mx=max(mx,f[x]+f[to[i]]+d[i]);//求经过该点的直径
f[x]=max(f[x],f[to[i]]+d[i]);//更新该点的最深路
}
}
断环为链,优先队列求解
per(i,1,n)
{
if(ck[i]) continue;
c=0,dfs(i,-1);//找环
mx=0;
per(j,1,c) sol(lop[j],0);//搜索每个子树
per(j,c+1,c*2) lop[j]=lop[j-c],dis[j]=dis[j-c];//断环为链的复制
per(j,2,c*2) s[j]=s[j-1]+dis[j];//每一个lop[x]点的dis[x]为他与前一个点之间的距离
h=1,t=0,q[1]=0;//求了前缀和,所以dis[x,y]=s[y]-s[x]
//ans=s[y]-s[x]+f[x]+f[y]
//优先队列维护 f[x]-s[x] 队首为最大
per(j,1,c*2)
{
while(h<=t&&j-q[h]>=c) ++h;
mx=max(mx,s[j]-s[q[h]]+f[lop[q[h]]]+f[lop[j]]);
while(h<=t&&f[lop[j]]-s[j]>=f[lop[q[t]]]-s[q[t]]) --t;
q[++t]=j;
}
ans+=mx;
}
完整代码
#include <bits/stdc++.h>
#define per(i,a,b) for(int i(a);i<=b;++i)
using namespace std;
const int N=2e6+10;
int hd[N],nx[N<<1],to[N<<1],d[N<<1],id=1,rt,lop[N],dis[N],c;
int q[N];
long long f[N],s[N<<1],mx;
bitset<N>ck,b;
void addd(int x,int y,int z){to[++id]=y,d[id]=z,nx[id]=hd[x],hd[x]=id;}
int dfs(int x,int ii)
{
if(ck[x])
{
rt=x;
return 1;
}
ck[x]=1;
int fg;
for(int i=hd[x];i;i=nx[i])
{
if(i==ii) continue;
fg=dfs(to[i],i^1);
if(fg)
{
if(fg==1)
{
lop[++c]=x,dis[c]=d[i],b[x]=1;
if(rt!=x) return 1;
}
return 2;
}
}
return 0;
}
// int dfn[N],idd;
// struct aaa{
// int x,w;
// }fa[N];
// void dfs(int x)
// {
// dfn[x]=++idd;
// for(int i=hd[x];i;i=nx[i])
// {
// if(dfn[to[i]])
// {
// if(dfn[to[i]]<dfn[x]) continue;
// lop[++c]=to[i],dis[c]=d[i],b[to[i]]=1;
// for(int y=to[i];y!=x;y=fa[y].x) lop[++c]=fa[y].x,dis[c]=fa[y].w,b[fa[y].x]=1;
// }
// else
// {
// fa[to[i]].x=x,fa[to[i]].w=d[i];
// dfs(to[i]);
// }
// }
// }
void sol(int x,int fa)
{
ck[x]=1;//dfs(x,ii)只能找到环,并不能遍历该树内所有点,有的ck[x]没被设成1
for(int i=hd[x];i;i=nx[i])
{
if(to[i]==fa||b[to[i]]) continue;
sol(to[i],x);
mx=max(mx,f[x]+f[to[i]]+d[i]);
f[x]=max(f[x],f[to[i]]+d[i]);
}
}
signed main()
{
int n,y,z,h,t;
long long ans=0;
cin>>n;
per(i,1,n) scanf("%d%d",&y,&z),addd(i,y,z),addd(y,i,z);
per(i,1,n)
{
if(ck[i]) continue;
c=0,dfs(i,-1);
mx=0;
per(j,1,c) sol(lop[j],0);
per(j,c+1,c*2) lop[j]=lop[j-c],dis[j]=dis[j-c];
per(j,2,c*2) s[j]=s[j-1]+dis[j];
h=1,t=0,q[1]=0;
per(j,1,c*2)
{
while(h<=t&&j-q[h]>=c) ++h;
mx=max(mx,s[j]-s[q[h]]+f[lop[q[h]]]+f[lop[j]]);
while(h<=t&&f[lop[j]]-s[j]>=f[lop[q[t]]]-s[q[t]]) --t;
q[++t]=j;
}
ans+=mx;
}
printf("%lld\n",ans);
return 0;
}
2.一棵树上,有一个环连向定点
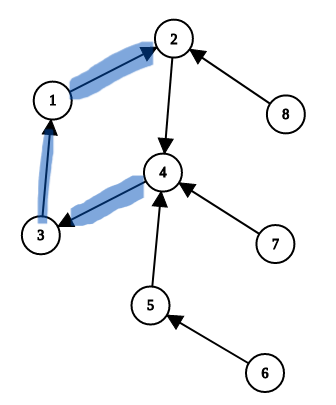
创世纪(AcWing359)
分情况讨论,是否选 \(rt\),树形dp:
void DP(int x) {
dp[x][0] = 0;
vis[x] = 1;
int cost = 1e9;
for(int i = head[x];i;i = nex[i]) {
int y = to[i];
if(y == root) continue;
DP(y);
cost = min(cost,max(dp[y][1],dp[y][0]) - dp[y][0]);
dp[x][0] += max(dp[y][1],dp[y][0]);
}
dp[x][1] = dp[x][0] - cost + 1;
if(x == fa[root] && flag) { //不选root,那么fa[root]选不选都能可以被限制。
dp[x][1] = dp[x][0] + 1;
}
}
void sol()
{
flag = 0;
DP(root);//选rt
res = dp[root][1];
flag = 1;
DP(root);//不选rt
res = max(res,dp[root][0]);
ans += res;
}
代码
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
const int maxn = 1e6 + 7;
int head[maxn],nex[maxn],to[maxn],tot;
void add(int x,int y) {
to[++tot] = y;
nex[tot] = head[x];
head[x] = tot;
}
int fa[maxn],vis[maxn];
int root,flag;
int dp[maxn][2];
void DP(int x) {
dp[x][0] = 0;
vis[x] = 1;
int cost = 1e9;
for(int i = head[x];i;i = nex[i]) {
int y = to[i];
if(y == root) continue;
DP(y);
cost = min(cost,max(dp[y][1],dp[y][0]) - dp[y][0]);
dp[x][0] += max(dp[y][1],dp[y][0]);
}
dp[x][1] = dp[x][0] - cost + 1;
if(x == fa[root] && flag) { //不选root,那么fa[root]选不选都能可以被限制。
dp[x][1] = dp[x][0] + 1;
}
}
int main() {
int n;scanf("%d",&n);
for(int i = 1;i <= n;i++) {
int x;scanf("%d",&x);
add(x,i);
fa[i] = x;
}
int ans = 0;
for(int i = 1;i <= n;i++) {
if(vis[i]) continue;
int res = 0;
root = i;
while(!vis[fa[root]]) {//往上跳找环
vis[root] = 1;
root = fa[root];
}
flag = 0;
DP(root);//选rt
res = dp[root][1];
flag = 1;
DP(root);//不选rt
res = max(res,dp[root][0]);
ans += res;
}
printf("%d\n",ans);
return 0;
}
仙人掌图
每条边仅在一个环中,不存在两个环有重边
将每一个环看做一个大点,进行缩环(仙人掌图\(\to\) 仙人掌树)
两点距离计算:找x,y的lca,同时变换x,y(最后x,y为z的子节点),记录原始位置a=x,b=y
分两种情况:
1.x,y在同一个环上
2.不在环上,直接求\(ans=dis[x]+dis[y]-(2*dis[lca(a,b)])\)
仙人掌图各点到根的距离可用spfa求
dfs,如果过程中发现\(dfn[to[i]]<dfn[x]\) 则成环,缩环
void circle(int s,int t,int line)
{
ck[line]=ck[line^1]=1;
c[++c[0]]=d[line];
for(int i=t;i!=s;i=to[mp[i]^1])
{
cir[i]=c[0];
ck[mp[i]]=ck[mp[i]^1]=1;
c[c[0]]+=d[mp[i]];
addd(s,i,0),addd(i,s,0);
}
}
void dfs(int x)
{
dfn[x]=++num;
for(int i=hd[x];i;i=nx[i])
{
if(i==(mp[x]^1)) continue;
if(!dfn[to[i]])
{
mp[to[i]]=i;
ds[to[i]]=ds[x]+d[i];
dfs(to[i]);
}
else if(dfn[to[i]]<dfn[x]) circle(to[i],x,i);
}
}
dfs(1)
重建仙人掌树,处理倍增数组
void rebuild(int x,int fa)
{
dep[x]=dep[fa]+1;
f[x][0]=fa;
per(i,1,19) f[x][i]=f[f[x][i-1]][i-1];
for(int i=hd[x];i;i=nx[i])
{
if(to[i]==fa||ck[i]) continue;
rebuild(to[i],x);
}
}
回答询问
int lca(int &x,int &y)
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=19;i>=0;--i) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
if(x==y) return x;
for(int i=19;i>=0;--i) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
per(i,1,q)
{
scanf("%d%d",&x,&y);
a=x,b=y,z=lca(x,y);
if(cir[x]&&cir[y]&&cir[x]==cir[y])
{
z=abs(ds[x]-ds[y]);
printf("%d\n",dis[a]-dis[x]+dis[b]-dis[y]+min(z,c[cir[x]]-z));
}
else printf("%d\n",dis[a]+dis[b]-(2*dis[z]));
}
代码
#include <bits/stdc++.h>
#define per(i,a,b) for(int i(a);i<=b;++i)
using namespace std;
const int N=1e4+10,M=12010*4;
int hd[N],nx[M],to[M],d[M],id=1,dis[N],dep[N],ds[N];
int dfn[N],c[M],cir[N],f[N][20],mp[N],num;
void addd(int x,int y,int z){to[++id]=y,d[id]=z,nx[id]=hd[x],hd[x]=id;}
bitset<M>ck;
queue<int>q;
void spfa()
{
int x;
memset(dis,0x3f,sizeof(dis));
dis[1]=0,ck[1]=1;
q.push(1);
while(!q.empty())
{
x=q.front(),q.pop();
ck[x]=0;
for(int i=hd[x];i;i=nx[i])
{
if(dis[to[i]]>dis[x]+d[i])
{
dis[to[i]]=dis[x]+d[i];
if(!ck[to[i]])
{
ck[to[i]]=1;
q.push(to[i]);
}
}
}
}
}
void circle(int s,int t,int line)
{
ck[line]=ck[line^1]=1;
c[++c[0]]=d[line];
for(int i=t;i!=s;i=to[mp[i]^1])
{
cir[i]=c[0];
ck[mp[i]]=ck[mp[i]^1]=1;
c[c[0]]+=d[mp[i]];
addd(s,i,0),addd(i,s,0);
}
}
void dfs(int x)
{
dfn[x]=++num;
for(int i=hd[x];i;i=nx[i])
{
if(i==(mp[x]^1)) continue;
if(!dfn[to[i]])
{
mp[to[i]]=i;
ds[to[i]]=ds[x]+d[i];
dfs(to[i]);
}
else if(dfn[to[i]]<dfn[x]) circle(to[i],x,i);
}
}
void rebuild(int x,int fa)
{
dep[x]=dep[fa]+1,f[x][0]=fa;
per(i,1,19) f[x][i]=f[f[x][i-1]][i-1];
for(int i=hd[x];i;i=nx[i])
{
if(to[i]==fa||ck[i]) continue;
rebuild(to[i],x);
}
}
int lca(int &x,int &y)
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=19;i>=0;--i) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
if(x==y) return x;
for(int i=19;i>=0;--i) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
signed main()
{
int n,m,q,x,y,z,a,b;
cin>>n>>m>>q;
per(i,1,m) scanf("%d%d%d",&x,&y,&z),addd(x,y,z),addd(y,x,z);
spfa();
ck.reset();
dfs(1);
rebuild(1,0);
per(i,1,q)
{
scanf("%d%d",&x,&y);
a=x,b=y,z=lca(x,y);
if(cir[x]&&cir[y]&&cir[x]==cir[y])
{
z=abs(ds[x]-ds[y]);
printf("%d\n",dis[a]-dis[x]+dis[b]-dis[y]+min(z,c[cir[x]]-z));
}
else printf("%d\n",dis[a]+dis[b]-(2*dis[z]));
}
return 0;
}

