网络流
1.网络流(网络最大流)
-
网络(自来水管道网 ):一张有向图,其上的 边权 称为容量。拥有一个源点和汇点。
-
流(水流): 每条边上的流不能超过它的容量,对于除源点汇点以外的所有点,流入量=流出量
从源点流出,全部流入汇点(假设源点流出的流量足够多)
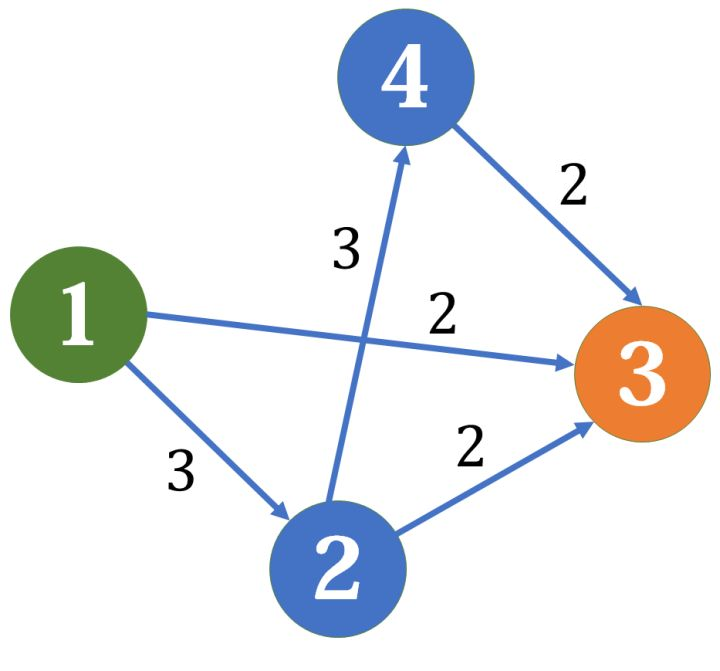
增广路:从源点到汇点的路径,其上所有边的残余容量均大于0
每找到一条增广路,增加的流量=这条路径上所有容量的最小值
残余容量:增广路上扣除 增加的流量 后的 剩余
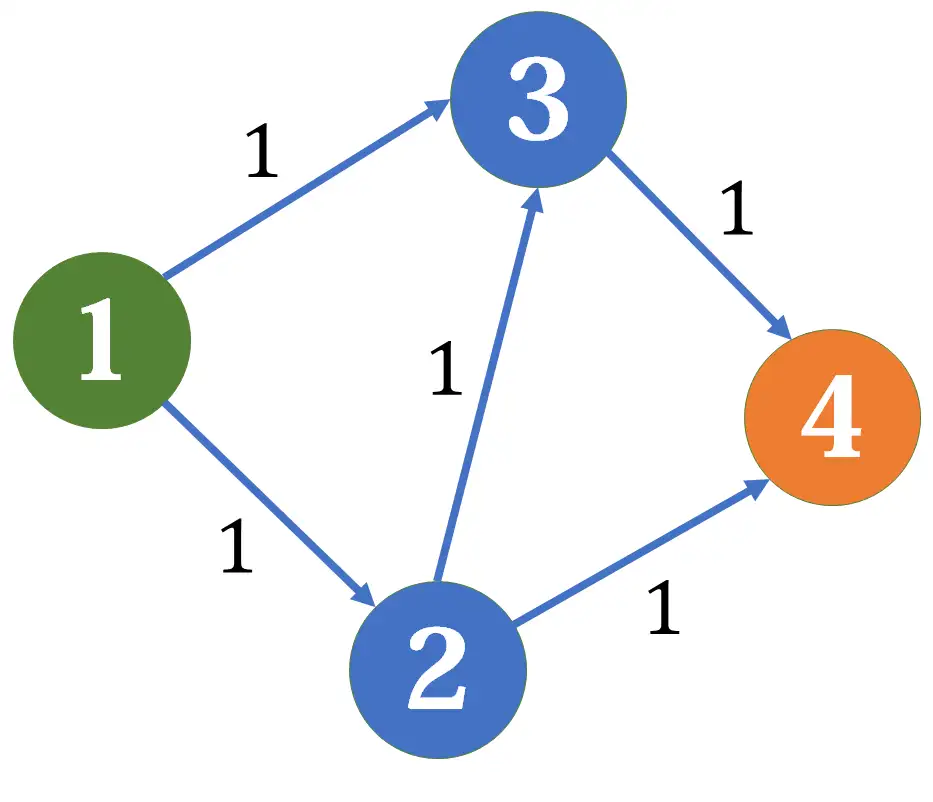
若选择1 \(\to\) 2 \(\to\) 3 \(\to\) 4 ,求得最大流=1
若选择1 \(\to\) 3 \(\to\) 4 ,1 \(\to\) 2 \(\to\) 4 最大流=2
反向边:在建边的同时,在反方向建一条边权为0的边(抵消,反悔机制)
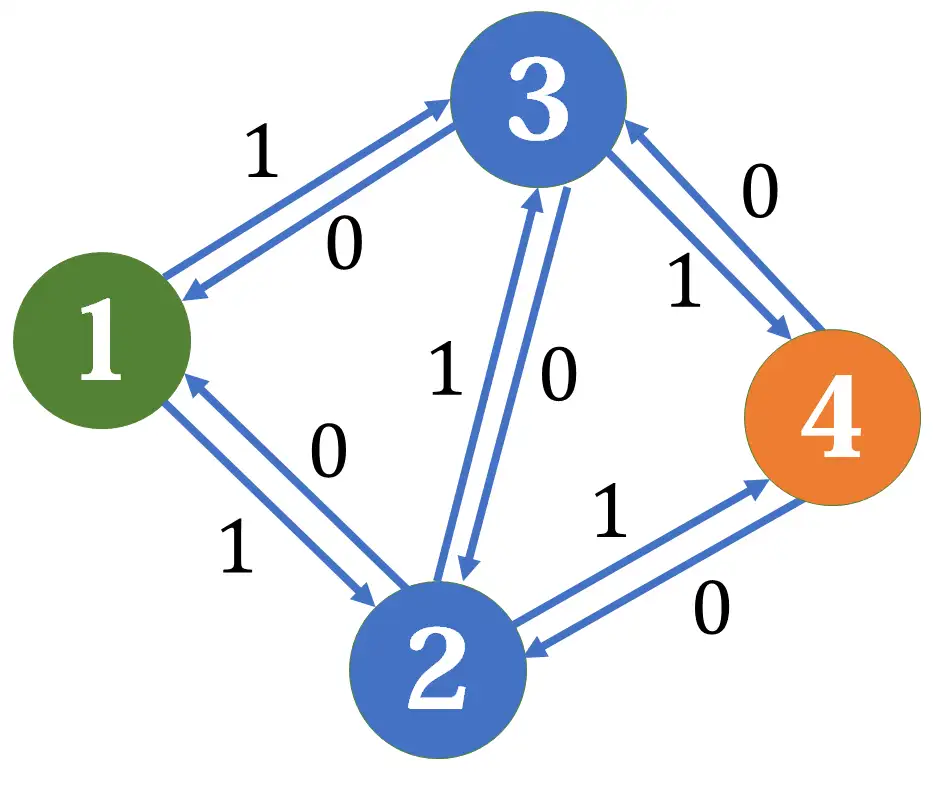
Ford-Fulkerson:
深搜 \(O(ef)\) 边数×最大流
int n, m, s, t; // s是源点,t是汇点
bool ck[N];
int dfs(int x = s, int res = INF)
{
if (x == t) return res; // 到达终点,返回这条增广路的流量
ck[x] = 1;
for (int i=hd[x];i;i=nx[i])
{
// 返回的条件是残余容量大于0、未访问过该点、且接下来可以达到终点(递归地实现)
// 传递下去的流量是边的容量与当前流量中的较小值
if (d[i] > 0 && !ck[to] && (c = dfs(to[i], min(d[i], res))) != -1)
{
d[i] -= c;
d[i^1] += c;
// 这是链式前向星取反向边的一种简易的方法
// 建图时要把cnt置为1,且要保证反向边紧接着正向边建立
return c;
}
}
return -1; // 无法到达终点
}
inline int FF()
{
int ans = 0, c;
while ((c = dfs()) != -1)
{
memset(ck, 0, sizeof(ck));
ans += c;
}
return ans;
}
Edmond-Karp:
广搜 \(O(n e^2)\) 点数 × 边数的平方
int n, m, s, t, last[MAXN], flow[MAXN];
inline int bfs()
{
memset(last, -1, sizeof(last));
queue<int> q;
q.push(s);
flow[s] = INF;
while (!q.empty())
{
int p = q.front();
q.pop();
if (p == t) /*到达汇点,结束搜索*/ break;
for (int i=hd[x];i;i=nx[i])
{
if (d[i] > 0 && last[to[i]] == -1) // 如果残余容量大于0且未访问过(所以last保持在-1)
{
last[to[i]] = i;
flow[to[i]] = min(flow[p], vol);
q.push(to);
}
}
}
return last[t] != -1;
}
inline int EK()
{
int maxflow = 0;
while (bfs())
{
maxflow += flow[t];
for (int i = t; i != s; i = to[last[i] ^ 1]) // 从汇点原路返回更新残余容量
{
edges[last[i]].w -= flow[t];
edges[last[i] ^ 1].w += flow[t];
}
}
return maxflow;
}
Dinic:
BFS分层,DFS寻找
多路增广,当前弧优化(一条边被走过一遍之后不会再走)
#include <bits/stdc++.h>
#define per(i,a,b) for(int i(a);i<=b;++i)
using namespace std;
const int N=210,M=5010,inf=0x3f3f3f3f;
int s,t,hd[N],to[M<<1],nx[M<<1],d[M<<1],id=1,dis[N],cur[N]/*hd*/;
void addd(int x,int y,int z){to[++id]=y,d[id]=z,nx[id]=hd[x],hd[x]=id;}
queue<int>q;
bool bfs()
{
memset(dis,-1,sizeof(lv));//分层图
lv[s]=0;
memcpy(cur,hd,sizeof(hd));//当前弧优化(一条边被走过一遍之后不会再走)
q.push(s);
int x;
while(!q.empty())
{
x=q.front(),q.pop();
for(int i=hd[x];i;i=nx[i])
{
if(d[i]&&dis[to[i]]==-1)
{
dis[to[i]]=dis[x]+1;
q.push(to[i]);
}
}
}
return dis[t]!=-1;
}
long long dfs(int x=s,long long res=LONG_LONG_MAX)
{
if(x==t) return res;
long long rs=res,c;
for(int i=cur[x];i&&rs;i=nx[i])//多路增广
{
cur[x]=i;
//如果该点被增广之后,rs还>0;
//说明要么该边容量用完,要么该边不能到达t
//所以该边可以删去
if(d[i]&&dis[to[i]]==dis[x]+1)
{
c=dfs(to[i],min((long long)d[i],rs));
rs-=c;
d[i]-=c,d[i^1]+=c;
}
}
return res-rs;
}
signed main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n,m,x,y,z;
cin>>n>>m>>s>>t;
per(i,1,m) scanf("%d%d%d",&x,&y,&z),addd(x,y,z),addd(y,x,0);
long long ans=0;
while(bfs()) ans+=dfs();
printf("%lld\n",ans);
return 0;
}
最小割最大流定理
从网络中选择一些边,删去这些边后,剩下两个不连通的点集,分别包括源点和汇点
最小割:删去边的容量和最小
神奇定理:最小割=最大流
一个比喻,割就是恐怖分子切断自来水厂到你家之间的水管 (你们恐怖分子就这点志向吗?),切断每个水管的代价就是水管的宽度(边的容量)。然后当代价最小时,从切断的水管中流出的流量之和就是最大流。
试题库问题 (洛谷2763 )
题意:
n道题,每道题属于p个类别;从题库中抽取m道题,每个类别\(a_i\)道
思路:
利用网络流的反悔机制,进行匹配
S \(\to\) 类别(k) 边权\(a_i\)
$k_i \to $ 题(n) 边权 1
题 \(\to\) T 边权 1
最大流=m 有解
输出:枚举题的类别 (1~k) 如果\(dis[k,x]=0\) 表示 x 被选入了第 k 类题
方格取数问题(洛谷2774)
目标:
从方格中取数,使任意两个数所在方格没有公共边
思路
需要舍弃一些点,使得剩下的点满足 任意两个数所在方格没有公共边
最大和=全局和-舍弃和,要使舍弃和最小 \(\Longrightarrow\)最小割=最大流
转化
将方格图转换为网络图
方格分为两类(横纵坐标之和的奇偶)相邻的方格横纵坐标奇偶性一定不同
if((i+j-1)&1)//偶
{
addd(s,e(i,j),x),addd(e(i,j),s,0);//x为该格权值
per(k,0,3)
{
x=i+f[k][1],y=j+f[k][0];
if(b(x,1,n)&&b(y,1,m))
addd(e(i,j),e(x,y),inf),addd(e(x,y),e(i,j),0);//互斥的方格连边
}
}
else addd(e(i,j),t,x),addd(t,e(i,j),0);
当图符合要求的时候,S,T 不连通,分为两个子图
ans= sum - 最大流
参考文章:算法学习笔记(28): 网络流
2.费用流(最小费用最大流)
费用= 每条边的流量 × 单位流量的费用
\(Cost(flow)=\sum_{<x,y>∈E}cost(x,y) × flow(x,y)\)
MCMF( spfa找最短路,回溯更新 )
bool spfa()//寻找源点到汇点的最小费用路 (以费用为边权,找最短路)
{
int x;
ck.reset();
memset(dis,0x3f,sizeof(dis));
dis[s]=0,q.push(s);
while(!q.empty())
{
x=q.front(),q.pop();
ck[x]=0;
for(int i=hd[x];i;i=nx[i])
{
if(dis[to[i]]>dis[x]+c[i]&&d[i]>0)
{
dis[to[i]]=dis[x]+c[i];
pre[to[i]]={x,i};//从x点经过i边到达了 当前点 (to[i])
if(!ck[to[i]])
{
ck[to[i]]=1;
q.push(to[i]);
}
}
}
}
return dis[t]!=inf;
}
void sol()
{
int ans=0;
int res,v;
while(spfa())
{//从记录的路径进行回溯更新
res=inf,v=t;
while(v!=s)
{
res=min(res,d[pre[v].i]);//最大流
v=pre[v].x;
}
v=t;
while(v!=s)
{
d[pre[v].i]-=res,d[pre[v].i^1]+=res;
v=pre[v].x;
}
ct+=dis[t]*res;
ans+=res;
}
}
3.最大权闭合子图
太空飞行计划(洛谷2762)
闭合子图
对于有向图 ,\(G(V,E)\) 它的一个闭合子图是一个点集,并且满足点集内所有的点,他们的出边指向的点都是点集内的点,然后将出边添加上,就是一个子图了。(入边无所谓)
闭合子图 \(\to\) 网络流
建一个源点,和一个汇点,
源点连向权值为正的点,流量为点权
权值为负的点向汇点连一条边,流量为点权的绝对值
点与点之间的边不变,流量为 INF
简单割(最小割):只割源点出去的边或到汇点的边。
目的:每一个S出发的边只能流向自己
割完之后 \(\Longrightarrow\) 每个实验所需的仪器都在S的闭合子图里
最大权闭合子图
设:\(v_1\) 为闭合子图 ,\(v_2\) 为闭合子图的补集
割的流量:\(C[S,T]=C[v_1,T]+C[S,v_2]=\sum_{v\in v_1^-} W_v+\sum_{v\in v_2^+} W_v\)
闭合子图权值:\(w_1=\sum_{v\in v_1^+} W_v-\sum_{v\in v_1^-} W_v\)
\(C[S,T]+W_1=\sum_{v\in v_1^+} W_v+\sum_{v\in v_2^+} W_v=\sum_{v\in v^+} W_v\)
\(\therefore 闭合子图最大权 W_1=\sum_{v\in v^+} -C[S,T]\)
求\(C[S,T]\) 最小,即为最小割
参考:最大权闭合子图
4.拆点
1.入点,出点
求割点的时候,可以将点拆成入点和出点,割掉中间连接的边就相当于割掉了点
奶牛的电信(洛谷1345)
将每个点拆成两个,当这两个点之间的边被割,代表改电脑坏了
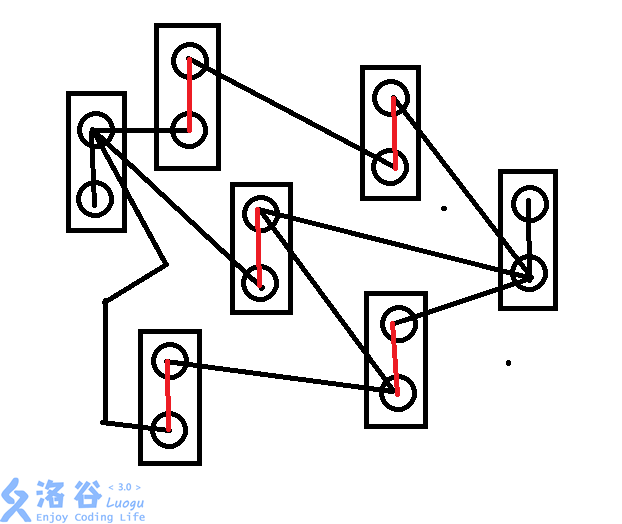
教辅的组成(洛谷1231)
将书拆点,练习册连书的入点,书的出点连对应的答案
魔术球问题(洛谷2765)
将一个球拆成入点出点
源点->入点
若两个数的和为平方数,入点连向出点
出点->汇点
边权都为 1
一个一个加入点,在之前的基础上跑最大流,如果流量=0,表示该点没法往柱子上放了,sum+=1,当sum=n的时候停止
玄学找规律:每个数枚举,能放在已有柱子上就直接放,不能放就开新柱子,模拟可A。证明
参考:网络流建模基础
5.点的构造
[HEOI2016/TJOI2016]游戏 (洛谷2825)
#***
*#**
**#*
xxx#
先不考虑硬石头,每摆放一个炸弹,他所在的行和列不能摆放炸弹
问题可以转换成二分图匹配,行(s)和列(t)匹配
硬石子:将一行/列可以分成两行/列
分别处理行和列的点构造,能放炸弹的点进行加边,二分图匹配
#include <bits/stdc++.h>
#define per(i,a,b) for(int i(a);i<=b;++i)
using namespace std;
const int E=55,N=3010,M=3010,inf=0x3f3f3f3f;
int s,t,hd[N],to[M<<1],nx[M<<1],id=1,match[N];
void addd(int x,int y){to[++id]=y,nx[id]=hd[x],hd[x]=id;}
int x[E][E],y[E][E];
char mp[E][E];
bitset<N>ck;
bool fd(int x)
{
for(int i=hd[x];i;i=nx[i])
{
if(!ck[to[i]])
{
ck[to[i]]=1;
if(!match[to[i]]||fd(match[to[i]]))
{
match[to[i]]=x;
return 1;
}
}
}
return 0;
}
signed main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n,m,nt=0,mt=0;
bool fg=1;
pair<int,int>ls;
ls=make_pair(0,0);
cin>>n>>m;
per(i,1,n)
{
cin>>mp[i]+1;
per(j,1,m)
{
if(mp[i][j]=='#')
{
fg=1;
continue;
}
if(!fg)
{
if(mp[i][j]!='X')
{
x[i][j]=x[ls.first][ls.second];
ls=make_pair(i,j);
}
}
else if(mp[i][j]!='X')
{
x[i][j]=x[ls.first][ls.second]+1;
nt++;
ls=make_pair(i,j);
fg=0;
}
}
fg=1;
}
fg=1;
ls=make_pair(0,0);
per(i,1,m)
{
per(j,1,n)
{
if(mp[j][i]=='#')
{
fg=1;
continue;
}
if(!fg)
{
if(mp[j][i]!='X')
{
y[j][i]=y[ls.second][ls.first];
ls=make_pair(i,j);
}
}
else if(mp[i][j]!='X')
{
y[j][i]=y[ls.second][ls.first]+1;
mt++;
ls=make_pair(i,j);
fg=0;
}
}
fg=1;
}
per(i,1,n) per(j,1,m) if(mp[i][j]=='*') addd(x[i][j],y[i][j]+nt);
int ans=0;
per(i,1,nt)
{
ck.reset();
if(fd(i)) ++ans;
}
printf("%d\n",ans);
return 0;
}


