博弈论

博弈论

前置芝士

N状态(必胜状态)

P状态(必败状态)

• 所有的终止都为必败（P) 状态
• 任意 **N ** 状态，存在至少一条路径可以转移到 P 状态
• 任意P状态只能转移到 N 状态

1.取石子游戏B

一共 \(n\) 颗石子，游戏双方轮流取石子；
每人每次取走若干颗石子（最少取 1 颗，最多取 m 颗）；
石子取光，则游戏结束； 最后取石子的一方为胜。

巴什博弈（Bash game）

问题描述：

有一堆总数为\(n\)的物品，2名玩家轮流从中拿取物品。
每次至少拿1件，至多拿\(m\)件，不能不拿，最终将物品拿完者获胜。
——减法博弈，有限的，完全信息
∴有必胜策略

分析:

①若n<m+1，至多为m件物品。先手方行动，可以一次取完→获胜，先手必胜。
②若n=m+1，先手一定取不完，所以后手必胜。

对于所有n，设\(n=k(m+1)+r\)，\(r∈[0,m+1)\)

当\(r=0\)时，\(n=k(m+1)\)，若先手取了x个，后手只需取m+1-x个，就能将n变成 \((k-1)(m+1)\)，直到n=m+1，所以此时后手必胜

当\(r \neq 0\)时，先手取走r个物品，就变成\(r=0\)状态了，此时先手必胜

#include <bits/stdc++.h>
#define per(i, a, b) for (int i(a); i <= b; ++i)
using namespace std;
int main() 
{
    // freopen(".in","r",stdin);
    // freopen(".out","w",stdout);
    int n, k;
    cin >> n >> k;
    if (n % (k + 1) == 0) puts("2");
    else puts("1");
    return 0;
}

结论

若\(n\bmod (m+1)=0\) 后手必胜
否则先手必胜。

变式：

若将规则改为取完者败。

相当于将n变为n + 1，先取完n-1个物品者获胜

∴若\(n\bmod (m+1)=1\) 后手必胜
否则先手必胜。

2.取石子游戏 #（过渡）

一个集合S={\(p_1,p_2,...,p_k\) }(k∈Z^*)，A , B 在游戏的时候取走的石子数必须是集合里的数，其他条件不变。

SG函数

\(SG(x)=mex\{SG(u)|u为x的后继状态\}\)

\(mex(A)=min\{k|k\in∁_NA\}\) mex(A)为不属于该集合的最小自然数

如图，S={2,5}，n=10，画出的图红色的表为每个状态的SG值

• SG值非0的节点可以走向0

• ​ 0的节点只能走向非0

SG(n)值为0时，先手必败;
否则先手必胜。

某点SG值为k时，它一定可以转移到\([0,k-1]\) (由mex定义可知)

int sg(int x)
{
    if(f[x]!=-1) return f[x];
    unordered_set<int>st;
    per(i,1,k) if(x>=s[i]) st.insert(sg(x-s[i]));
    for(int i=0;;++i) if(!st.count(i)) return f[x]=i;
}
求sg(n)即可

3.取石子游戏A

k堆石子，每堆石子数量给定。游戏双方轮流取石子；
每人每次选一堆石子，并从中取走若干颗石子（至少取 1 颗）；
所有石子被取完，则游戏结束； 如果轮到某人取时已没有石子可取，那此人算负。

Nim

将每堆石子数量用二进制表达

注：每一堆的石子数等于当前堆的SG值（对于每堆可以任选取几个石子），因为没规定能取几个，所以SG值可以任意减小。

e.g. 三堆，分别为 7,5,12
二进制：
7 : 0 1 1 1
5 : 0 1 0 1
12： 1 1 0 0
——————————
异或和⊕：1 1 1 0

• 最终的 P 状态，一定是异或和为0（没有石子可取了）

• 所以异或和不为0的状态就是 N 状态(一定可以转移到 P 状态)

• P 状态只能转移到 N 状态（异或和为0时，无论怎么取，都会把异或和变成非0）

异或和为0，先手必败；
否则先手必胜。

#include <bits/stdc++.h>
#define per(i,a,b) for(int i(a);i<=b;++i)
using namespace std;
const int N=5e4+10;
int main()
{
	// freopen(".in","r",stdin);
    // freopen(".out","w",stdout);
    int n,x=0,e;
    cin>>n;
    per(i,1,n) scanf("%d",&e),x^=e;
    if(x) puts("win");
    else puts("lose");
    return 0;
}

4.取石子游戏C

先给定一个集合\(S\)，有k个元素。然后有n堆石子，每堆分别有\(h_i\)个，每次都可以从某一堆中取出\(x\)个石子（这里的\(x\)规定必须是合\(S\)中的一个元素），两个人轮流取最优，问是否先手必胜。

综合2,3

#include <bits/stdc++.h>
#define per(i,a,b) for(int i(a);i<=b;++i)
using namespace std;
int s[110],f[10010],k;
int sg(int x)//T2思路
{
    if(f[x]!=-1) return f[x];
    unordered_set<int>st;
    per(i,1,k) if(x>=s[i]) st.insert(sg(x-s[i]));
    for(int i=0;;++i) if(!st.count(i)) return f[x]=i;
}
int main()
{
	// freopen(".in","r",stdin);
    // freopen(".out","w",stdout);
    int n,x=0,e;
    cin>>k;
    per(i,1,k) scanf("%d",s+i);
    memset(f,-1,sizeof(f));
    cin>>n;
    per(i,1,n)//T3思路
    {
        scanf("%d",&e);
        x^=sg(e);
    }
    if(x) puts("Yes");
    else puts("No");
    return 0;
}

5.取石子游戏D

提示给出：如果\([a/b]>=2\)则先手必胜，而且可知：a%b=0时，也先手必胜
若不满足条件，从大的那堆取最多

阶梯博弈

有 \(n\) 堆石子，每堆石子的数量为\(x_1,x_2,x_3,...,x_n\) ，A 和 B 轮流行动，每次可以选第 \(k\) 堆中的任意多个石子放到第 \(k-1\) 堆中，第 1 堆中的石子可以放到第 0 堆中，最后无法行动的人为输。问 A 先手是否有必胜策略。

转化

将奇数阶梯看成n堆石子，从奇数堆移动到偶数堆看做拿走石子。
所以当开始的时候奇数阶梯上的石子数大于0，先手必胜

证明

假设我们是先手，首先我们按 Nim 中必胜的步骤将奇数阶梯上的一些石子移动到偶数阶梯上，使奇数阶梯的石子数的异或和为 。

如果对手选择移动奇数阶梯上的石子，那么我们依然可以像刚才一样行动；
如果对手选择移动偶数阶梯上的石子，那么我们就将他所移动到奇数阶梯的石子原封不动地移动到偶数阶梯上，也就相当于奇数阶梯的状态没有改变。

(最后状态为将所有石子都移动到了0上，等价于全部取完)

格鲁吉亚和鲍勃

从左到右有一排格子，其中一些格子中放有一个棋子。两个人轮流移动棋子 ，规定每个棋子只能向左移动，且不能跨过前面的棋子，并且一个格子最多可以包含一个棋子。最左边的棋子最多只能移动到第 1 个格子。不能移动棋子的人判负。问先手是否能赢。

把两个相邻棋子之间的空格个数当做一堆石子，相当于每次把移动的石子的左面的一个空格移到右面。

问题转换成左高右低的阶梯问题

#include <bits/stdc++.h>
#define per(i,a,b) for(int i(a);i<=b;++i)
using namespace std;
int a[1010],s[1010];
int main()
{
	// freopen(".in","r",stdin);
    // freopen(".out","w",stdout);
    int t,n,ans;
    cin>>t;
    while(t--)
    {
        ans=0;
        cin>>n;
        per(i,1,n) scanf("%d",a+i);
        sort(a+1,a+n+1);
        per(i,1,n) s[i]=a[i]-a[i-1]-1;//计算相邻棋子之间的空格数
        for(int i=n;i>=1;i-=2) ans^=s[i];//第n个棋子后面为第0个阶梯，从第n个空开始向前找奇数堆
        if(ans) puts("Georgia will win");
        else puts("Bob will win");
    }
    return 0;
}

D.Gra-Game

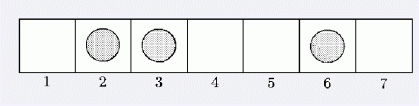
必败情况：m-1处有棋子，或m-n-1到m-2这个区间里全有石子（无论移动哪个棋子都会到m-1

https://www.cnblogs.com/f2021ljh/p/16849187.html#1巴什博弈bash-game

#include <bits/stdc++.h>
#define per(i,a,b) for(int i(a);i<=b;++i)
using namespace std;
const int N=1e6+10;
int a[N],s[N];
int main()
{
	// freopen(".in","r",stdin);
    // freopen(".out","w",stdout);
    int n,m,ans=0,sum=0,tot=0;
    cin>>m>>n;
    per(i,1,n) scanf("%d",a+i);
    if(a[n]==m-1)
    {
        for(int i=n+1;i;i--) if(a[i]-a[i-1]==1) ++ans;
        printf("%d\n",ans);
        return 0;
    }
    a[n+1]=m-1;
    for(int i=n;i;--i)
    {
        if(a[i+1]-a[i]==1) s[tot]++;
        else if(a[i+1]-a[i]==2) s[++tot]=1;
        else if((a[i+1]-a[i]-1)&1) s[tot+=3]=1;
        else s[tot+=2]=1;
    }
    for(int i=1;i<=tot;i+=2) sum^=s[i];
    if(!sum)
    {
        puts("0");
        return 0;
    }
    for(int i=1;i<=tot;i+=2) if((s[i]^sum)<s[i]) ++ans;
    for(int i=2;i<=tot;i+=2) if((s[i-1]^sum)>s[i-1]&&(s[i-1]^sum)<=s[i-1]+s[i]) ++ans;
    printf("%d\n",ans);
    return 0;
}