学习笔记：博弈论基础
0 一些定义与概念
公平组合游戏（Impartial combinatorial game, ICG）
公平组合游戏 满足：
- 由两名玩家交替移动；
- 在游戏进程的任意时刻，可以执行的合法行动与轮到哪名玩家无关；
- 不能行动的玩家判负。
Nim 游戏属于公平组合游戏。但常见的棋类大部分都不是公平组合游戏，因为双方执子不同，且判定胜负的规则有时也比较复杂。
游戏过程中面临的状态称为 局面。一局游戏中第一个行动的称为 先手，后一个行动的称为 后手。
如果在某一局面下，无论采取何种行动都会输掉游戏，即最后不能行动，则称该局面 必败。
在公平组合游戏中，一般以双方 采取最优策略 为前提。即如果当前局面下存在一种行动使得行动后对手必败，那么必定优先采取该行动。这时当前局面被称为 必胜。
博弈图
把一个 ICG 的所有状态抽象成一个个节点，如果一个状态能够通过游戏一方的一次行动变成另一个状态，那么由前一个状态到下一个状态连一条有向边。
这样会形成一个有向无环图，称为博弈图。
根据定义，有下面三条定理：
- 没有后继状态的状态是必败状态；
- 一个状态是必胜状态当且仅当存在 至少一个 必败状态为它的后继状态；
- 一个状态是必败状态当且仅当它的所有后继状态 均为 必胜状态。
1 巴什博弈（Bash Game）
问题
有一堆 \(n\) 个石子，A 和 B 轮流取石子，每一次最多可以取 \(m\) 颗，但 不能不取。取走最后一颗石子的人获胜。
如果 A 先取石子，请问 A 有没有一种必胜的策略？
分析
当 \(n\) 是 \(m+1\) 的倍数时，A 不论取多少个，B 都可以取若干个，使得两人取的石子总数为 \(m+1\)，于是最终一定是 B 最后一个取，所以 A 必败。
当 \(n\) 不是 \(m+1\) 的倍数时，A 先取 \(n\bmod (m+1)\) 个，使得局面变成上面的局面，只是变成了 B 先取，所以 A 必胜。
2 SG 函数
引入
定义一个集合 \(S=\{p_1,p_2,\dots,p_k\}(k\in\mathbb{N}_+)\)，A 和 B 在游戏的时候取走的石子数必须是 \(S\) 中的数，而不是 \(1\) 到 \(m\)，其他条件与 Bash 博弈相同。
那么，A 还有必胜策略吗？
有没有必胜策略，我们关键是要找到哪些状态是必胜状态，哪些状态是必败状态。不过，本题没有 Bash 博弈那么容易判断，因此我们需要引入一个新东西——SG 函数。
定义
首先，设 \(A\subset\mathbb{N}\)。定义对集合 \(A\) 的 mex(minimal excludant) 运算 \(\operatorname{mex}(A)\) 为不属于 \(A\) 的最小非负整数，即
对于博弈图中一个的状态 \(x\)，它有后继状态 \(y_1,y_2,\dots,y_k\)，那么定义 \(\operatorname{SG}(x)\) 为
终止状态的 SG 值为 \(0\)。
有向图游戏
有向图游戏是一个经典的博弈游戏——实际上，大部分的公平组合游戏都可以转换为有向图游戏，也就是在博弈图中进行有向图游戏。
有向图游戏的定义是：在一个有向无环图中，只有一个起点，上面有一个棋子，两个玩家轮流沿着有向边推动棋子，不能走的玩家判负。
SG 定理
我们定义整个 有向图游戏 \(G_i\) 的 SG 函数值 为游戏起点 \(s_i\) 的 SG 函数值，即 \(\operatorname{SG}(G_i)=\operatorname{SG}(s_i)\)。
对于 \(n\) 个有向图游戏 \(G_1,G_2,\dots,G_n\)，定义有向图游戏 \(G\) 的行动规则是任选某个有向图游戏 \(G_i\) 并行动一步。\(G\) 称为 有向图游戏 \(G_1,G_2,\dots,G_n\) 的和。
定义有向图游戏 \(G\) 的 SG 函数值为 \(G_1,G_2,\dots,G_n\) 的 SG 值的异或和。即
其中 \(\oplus\) 为异或运算。
定理 对于一个有向图游戏，局面 \(x\) 必胜当且仅当 \(\operatorname{SG}(x)>0\)；局面 \(x\) 必败当且仅当 \(\operatorname{SG}(x)=0\)。
这一定理被称作 Sprague-Grundy 定理(Sprague-Grundy Theorem), 简称 SG 定理。
理解：
首先，如果 \(x\) 是终止状态，\(x\) 必败，SG 值为 \(0\)。
如果存在某个后继局面的 SG 值为 \(0\)，即存在某个后继局面必败，那么由于 mex 运算，当前局面的 SG 值一定大于 \(0\)，即当前局面必胜；
如果不存在某个后继局面的 SG 值为 \(0\)，即所有后继局面必胜，那么由于 mex 运算，当前局面的 SG 值一定为 \(0\)，即当前局面必败。
具体可以用数学归纳法证明。
我们回到开始时的问题。
对于每一个状态，我们可以求出它的后继状态，进而求出起点的 SG 值。
3 Nim 游戏
问题
有 \(n\) 堆石子，石子数目分别为 \(x_1,x_2,\dots,x_n\)，A 和 B 两人每次可以选一堆石子取走任意多个，问 A 先手是否有必胜策略。
分析
定理 Nim 游戏先手必胜，当且仅当 \(x_1\oplus x_2\oplus\dots\oplus x_n\ne0\)，其中 \(\oplus\) 为异或运算。
证明 设 \(x_1\oplus x_2\oplus\dots\oplus x_n=x\)。我们称其为 Nim 和。
首先，所有东西都被取光是必败局面，此时满足 Nim 和为 \(0\)。
对于任意一个局面，如果 Nim 和不等于 \(0\)，我们设 \(x\) 的二进制表示下的最高位的 \(1\) 在第 \(k\) 位，那么至少存在一个 \(x_i\) 的第 \(k\) 位是 \(1\)。为了让 Nim 和变为 \(0\)，我们想要将 \(x_i\gets x_i\oplus x\)。由于 \(x_i\) 和 \(x\) 的最高位 \(1\) 都在第 \(k\) 位，所以 \(x_i\oplus x<x_i\)，所以可以把 \(x_i\) 取走若干个变为 \(x_i\oplus x\)。这样留给对手的局面就是 Nim 和为 \(0\) 的了。
对于任意一个局面，如果 Nim 和等于 \(0\)，那么无论如何取石子，Nim 和都会改变（可用反证法证明，如果 Nim 和不变，那么石子数也不变），所以一定会变成 Nim 和大于 \(0\) 的局面。
根据数学归纳法，Nim 和不等于 \(0\) 则为必胜局面，一定存在一种行动使得对手面临 Nim 和等于 \(0\) 的必败局面；Nim 和等于 \(0\) 则为必败局面，无论如何行动都会使得对手面临 Nim 和不等于 \(0\) 的必胜局面。
异或运算的性质：
- 交换律 \(x\oplus y=y\oplus x\)；
- 结合律 \((x\oplus y)\oplus z=x\oplus(y\oplus z)\)；
- 单位元 \(0\oplus x=x\)；
- 消去律 \(x\oplus x=0\)。
事实上，我们可以将一个有 \(x\) 个石子的堆视为节点 \(x\)，则当且仅当 \(y<x\) 时，节点 \(x\) 可以到达 \(y\)。那么，由 \(n\) 个堆组成的 Nim 游戏，就可以视为 \(n\) 个有向图游戏了。根据 SG 函数的定义，可以得出 \(\operatorname{SG}(x)=x\)。再根据 SG 定理，就可以得出上面关于 Nim 和的结论了。
模板题
代码
/*
http://poj.org/problem?id=2975
Nim 模板
问有多少种第一步使得后手必败
*/
#include <iostream>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
using namespace std;
const int N = 1e3 + 10;
int n, t, a[N], ans;
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
while (cin >> n, n) {
t = ans = 0;
f(i, 1, n) {
cin >> a[i];
t ^= a[i];
}
if (!t) {
cout << 0 << '\n';
continue;
}
f(i, 1, n) if (a[i] >= (a[i] ^ t)) ++ans; //a[i]变为a[i]^t, 从而使得异或和为0
cout << ans << '\n';
}
return 0;
}
4 拓展
POJ 2960 S-Nim（集合 Nim）
题意
在 Nim 游戏中，给定正整数构成的集合 \(S=\{s_1,s_2,\dots,s_k\}\)，要求每次取的石子数量只能是任意一个 \(s_i(0<i\le k)\)。问 A 先手能否获胜。
每组测试数据给定 \(k\) 和 \(s_1,s_2,\dots,s_k\)，给定 \(m\) 并进行 \(m\) 组询问，每组询问包含石子堆数 \(n\) 和每堆石子的数量 \(h_1,h_2,\dots,h_n\)。
对于每组测试数据，输出一行由 \(\texttt{W}\) 和 \(\texttt{L}\) 构成的长度为 \(m\) 的字符串，代表每组询问是先手必胜还是先手必败。
\(0<k\le100\)，\(0<s_i\le10000(0<i\le k)\)，\(0<m\le100\)，\(0<n\le100\)，\(0<h_i\le10000(0<i\le n)\)。
思路
类似上面引入 SG 时提出的问题，我们处理出所有状态的 SG 值，然后进行 Nim 游戏。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
using namespace std;
const int N = 1e2 + 10, M = 1e4 + 10;
int k, s[N], sg[M], m, n, h, sum;
bool vis[M];
void get_sg() {
memset(sg, 0, sizeof(sg));
f(i, 1, M) {
memset(vis, 0, sizeof(vis));
f(j, 1, k) {
if (i < s[j]) break;
vis[sg[i - s[j]]] = true; //由i能到达i-s[j]
}
f(j, 0, i) if (!vis[j]) {
sg[i] = j; //第一个不能到达的值
break;
}
}
return;
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
while (cin >> k, k) {
f(i, 1, k) cin >> s[i];
sort(s + 1, s + k + 1);
get_sg();
cin >> m;
f(i, 1, m) {
cin >> n;
sum = 0;
f(i, 1, n) {
cin >> h;
sum ^= sg[h];
}
cout << (sum ? 'W' : 'L');
}
cout << '\n';
}
return 0;
}
阶梯博弈（Staircase Nim）
问题
有 \(n\) 堆石子，每堆石子的数量为 \(x_1,x_2,\dots,x_n\)，A 和 B 轮流行动，每次可以选第 \(k\) 堆中的任意多个石子放到第 \(k−1\) 堆中，第 \(1\) 堆中的石子可以放到第 \(0\) 堆中，最后无法行动的人为输。问 A 先手是否有必胜策略。
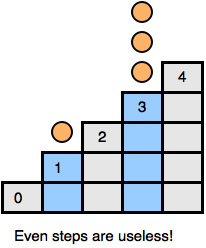
分析
其实阶梯博弈经过转化可以变为普通的 Nim。把所有奇数阶梯看成 \(N\) 堆石子，将石子从奇数阶梯移动到偶数阶梯可以理解为拿走石子，相当于几个奇数阶梯的石子在做 Nim。如果开始时 所有奇数阶梯上的石子数的异或和大于 \(0\)，先手只要将这个异或和变为 \(0\) 就可以必胜了。
为什么可以这样转化呢？
假设我们是先手，首先我们按 Nim 中必胜的步骤将奇数阶梯上的一些石子移动到偶数阶梯上，使奇数阶梯的石子数的异或和为 \(0\)。如果对手选择移动奇数阶梯上的石子，那么我们依然可以像刚才一样行动；如果对手选择移动偶数阶梯上的石子，那么我们就将他所移动到奇数阶梯的石子原封不动地移动到偶数阶梯上，也就相当于奇数阶梯的状态没有改变。
如此一直跟着后手做下去，我们一定可以最后一个移动石子使得对方再也无法行动，然后我们就赢了。
为什么是只对奇数堆做 Nim 就可以，而不是偶数堆呢？因为如果是对偶数堆做 Nim，对手移动奇数堆的石子到偶数堆，我们跟着移动这些石子到下一个奇数堆……那么最后是对手把这些石子移动到了第 \(0\) 堆，我们不能继续跟着移动，就只能去破坏原有的 Nim 而导致胜负关系的不确定。所以只要对奇数堆做 Nim 判断即可知道胜负情况。
例题 POJ 1704 Georgia and Bob
题意
从左到右有一排格子，其中一些格子中放有一个棋子。两个人轮流移动棋子 ，规定每个棋子只能向左移动，且不能跨过前面的棋子，并且一个格子最多可以包含一个棋子。最左边的棋子最多只能移动到第 \(1\) 个格子。不能移动棋子的人判负。问先手是否能赢。
思路
我们记录每一个棋子 最多向左移动的步数。如果把一个棋子向左移动，那么它能移动的步数变少，而它右边棋子能移动的步数变多。
如果 把步数看做是一堆石子 的话，向左移动就相当于是把石子由左边这一堆移动到右边这一堆。
我们发现这个问题就是左边高右边低的阶梯博弈。
所以我们只需要把从右往左数的所有奇数堆石子数取异或和就能判断是否必胜了。
事实上，我们也可以用上面分析经典阶梯博弈问题的思想来考虑。
我们把棋子按位置升序排列后，从后往前把他们 两两绑定成一对。如果总个数是奇数，就把最前面一个和边界（位置为 \(0\)）绑定。
在同一对棋子中，如果对手移动前一个，你总能对后一个移动相同的步数，所以不同的两对棋子之间有多少个空位置对最终的结果是没有影响的。我们只需要考虑同一对中的两个棋子之间有多少个空位置。
我们 把同一对中的两个棋子之间的空位置数看做一堆石子。那么移动后一个棋子就相当于是拿走石子，当两个棋子相邻的时候石子数变为 \(0\)。做普通的 Nim 即可。
（其实并没有平手的情况。。。）
代码
#include <iostream>
#include <algorithm>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
using namespace std;
const int N = 1e3 + 10;
int tt, n, sum, a[N];
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> tt;
while (tt--) {
int lst = 0;
sum = 0;
cin >> n;
f(i, 1, n) cin >> a[i];
sort(a + 1, a + n + 1);
f(i, 1, n) a[i] -= lst + 1, lst += a[i] + 1;
for (int i = 1 + ~(n & 1); i <= n; i += 2) sum ^= a[i];
cout << (sum ? "Georgia will win\n" : "Bob will win\n");
}
return 0;
}
例题 [POI2004] Gra
POI官网 | 洛谷 P8382 | 黑暗爆炸 2066 - vjudge | 码创未来
题意
有一排 \(1\times m\) 的方格，从左到右编号为 \(1\) 到 \(m\)，其中有 \(n\) 个方格上面有棋子，每个方格最多只能放一个棋子，第 \(m\) 个方格中没有棋子。
两个人交替移动棋子，每一次移动可以选择一个棋子，并把它移动到 它右边第一个未被占据的方格 中。第一个占据格子 \(m\) 的人获胜。两个人的行动一定采用最优策略。
如下图，一次移动可以把 \(2\) 移到 \(4\)、把 \(3\) 移到 \(4\) 或者把 \(6\) 移动到 \(7\)。
问先手有多少种移动是必胜的。
数据范围：\(2\le m\le10^9,1\le n\le10^6,n<m\)。
思路
首先考虑什么情况下必败。显然如果 \(m-1\) 处有棋子，那么任何一个人都可以走一步获胜，所以是必败局面。
那么什么情况下怎么走都是必败状态呢？显然是从 \(m-n-1\) 到 \(m-2\) 这个区间内全部有石子的情况，下一步无论移动哪个棋子都会到 \(m-1\)。所以这种情况是必胜局面，也就是终止的状态。
问题转化为：将所有 \(n\) 个石子移动到 \([m-n-1,m-2]\) 这个区间内，移动完最后一个石子的人胜利。
那么如何将问题转化为阶梯博弈的模型呢？
我们 将每一个空的方格设为一级台阶，空方格左边的连续棋子数即为台阶石子数（可能为 \(0\)）。
由于空方格数是不变的，所以台阶数也是不变的。我们把台阶从右到左标号。最后一个台阶即是 \(m-n-2\)。如下图。
对于每一次移动棋子的操作，如果把当前所在的一列连续棋子分为了 \(x\) 和 \(y\) 两部分长度，那么相当于是把石子往下一级台阶移动了 \(y\) 个，如下图。
然后我们来考虑题目中提出的问题。
在上面的阶梯博弈问题中，我们算出奇数阶梯上石子数的异或和 \(S\)，然后对于每一个奇数阶梯的石子数 \(s_i\)，将石子数变为 \(S\oplus s_i\)（如果可行的话）。对于偶数阶梯上的石子，我们也可以把一部分加到奇数阶梯 \(s_i\) 上使其变为 \(S\oplus s_i\)。统计这两种答案的个数即可。
但是……！题目中 \(m\) 的范围是不超过 \(10^9\)，所以显然把所有阶梯都遍历一遍是不能通过的。注意到有石子的阶梯数不超过 \(10^6\)，所以我们可以优化掉中间的很多空阶梯。具体来说，如果中间有奇数个空阶梯，就变成三个空阶梯；如果中间有偶数个空阶梯，就变成两个空阶梯。（一个空阶梯除外）
代码
（细节，细节，还是***细节！！！）
#include <iostream>
#include <algorithm>
#define f(x, y, z) for (int x = (y); (x) <= (z); ++(x))
#define g(x, y, z) for (int x = (y); (x) >= (z); --(x))
using namespace std;
const int N = 1e6 + 10;
int n, m, sum, tot, ans, a[N], step[N];
signed main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> m >> n;
f(i, 1, n) cin >> a[i];
// sort(a + 1, a + n + 1); //题目已经排好序了
if (a[n] == m - 1) {
int t = n + 1;
do --t, ++ans;
while (a[t] - a[t - 1] == 1);
return cout << ans << '\n', 0;
}
a[n + 1] = m - 1;
g(i, n, 1) { //从右到左构建台阶
if (a[i + 1] - a[i] == 1) ++step[tot];
else if (a[i + 1] - a[i] == 2) step[++tot] = 1;
else if ((a[i + 1] - a[i] - 1) & 1) step[tot += 3] = 1;
else step[tot += 2] = 1;
}
for (int i = 1; i <= tot; i += 2) sum ^= step[i];
if (!sum) return cout << 0 << '\n', 0;
for (int i = 1; i <= tot; i += 2)
if ((step[i] ^ sum) < step[i]) ++ans;
for (int i = 2; i <= tot; i += 2)
if ((step[i - 1] ^ sum) > step[i - 1] && (step[i - 1] ^ sum) <= step[i - 1] + step[i]) ++ans;
cout << ans << '\n';
return 0;
}
