poj2528(线段树+离散化)Mayor's posters

2016-08-15

题意：一面墙，往上面贴海报，后面贴的可以覆盖前面贴的。问最后能看见几种海报。

思路：可以理解成往墙上涂颜色，最后能看见几种颜色（下面就是以涂色来讲的）。这面墙长度为1~1000 0000，一千万，确实很大。暴力的话肯定不行，除非..（ you know）。

正确的解法是用线段树，不过还得加上离散化，因为数据太大10000000啊。

先说一下离散化，这个其实就是压缩，把范围压缩，举个例子:

输入：

1 3000 //涂第一种颜色范围从1~10000 下面同理

2000 7000 //第二种颜色

我们可以先把输入的数据范围压缩，假如输入的数据存到数组a[0]=1,a[1]=3000,a[2]=2000,a[3]=7000。

离散化（压缩）过程：

先把a[]从小到大排序。然后接着

把a数组里的数据映射到dis数组里，这样涂颜色（插入）的时候用dis[a[i]]。

压缩完之后建树的时候只需建1~4范围的树，而不用建1~7000的树。所以说离散化是必须的...懂嘞谬？

离散化完事后，再说说线段树，到底是个什么树呢？

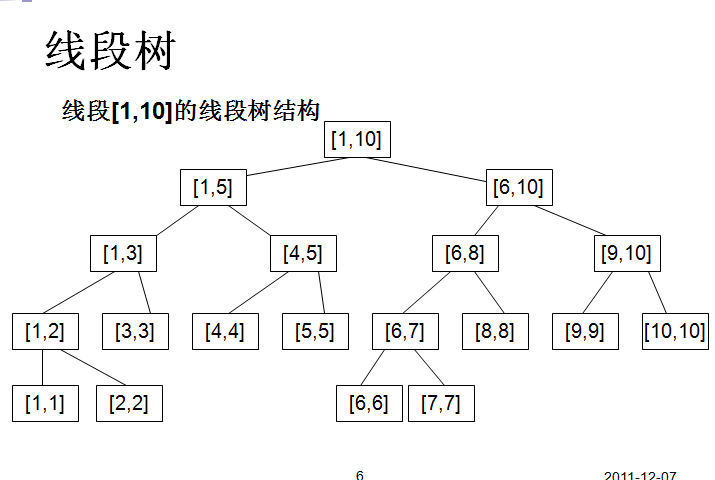
比如1~10这个线段，用二叉树的形式储存起来，

看图：

然后在每个节点加上各种信息，就可以用了，虽然空间大了但时间快了

对于这个问题线段树主要用了三个函数

void build(int p,int a,int b) //建树

void update(int p,int col,int a,int b)//插入颜色

void query(int p) //查询颜色

代码有详细解释

AC代码：

  1 #include <iostream>
  2 #include <cstring>
  3 #include <cstdio>
  4 #include <algorithm>
  5 using namespace std;
  6 
  7 const int MAXN=10005;
  8 
  9 bool tagcol[MAXN];   //标记颜色是否已经计算过
 10 
 11 int e[MAXN<<1];     //临时数组，把重复的数据去掉
 12 int ee[MAXN][2];    //直接输入数据的数组 存每张海报的范围的
 13 int dis[10000001];   //离散化之后的映射数组
 14 int cnt=0;           //颜色计数器
 15 
 16 struct node     //线段树节点
 17 {
 18     int l,r;    //l~r 范围
 19     int c;    //颜色（用1,2,3...表示）
 20 }LTnode[MAXN<<4];    //开数组的时候尽量开大点，开8倍就Runtime Error了，开16倍就过，虽然不知道为啥
 21 
 22 void build(int p,int a,int b)   //建树，p是节点下标，范围 a~b
 23 {
 24     LTnode[p].l=a;
 25     LTnode[p].r=b;
 26     LTnode[p].c=0;
 27     if(a==b)    //到叶子节点直接返回
 28     {
 29         return;
 30     }
 31 
 32     //继续递归建树
 33     int mid=(a+b)>>1;
 34     build(p<<1,a,mid);
 35     build(p<<1|1,mid+1,b);
 36     return;
 37 }
 38 void update(int p,int col,int a,int b)   //更新（插入）颜色，p是节点下标，col是颜色，a,b是要更新的范围
 39 {
 40     if(LTnode[p].l>=a&&LTnode[p].r<=b)   //如果当前节点范围 正好在a,b内，更新颜色 返回
 41     {
 42         LTnode[p].c=col;
 43         return;
 44     }
 45     if(LTnode[p].r<a||LTnode[p].l>b)   //如果当前节点范围和a,b没有交集
 46         return;
 47     if(LTnode[p].c>=0)   //当前节点和a,b有部分交集
 48     {
 49         LTnode[p<<1].c=LTnode[p<<1|1].c=LTnode[p].c;  //把当前节点的颜色传递给左右孩子节点，灰常重要
 50         LTnode[p].c=-1;    //-1代表有多种颜色
 51     }
 52     //继续处理左右孩子
 53     update(p<<1,col,a,b);
 54     update(p<<1|1,col,a,b);
 55     return;
 56 }
 57 
 58 void query(int p)   //查询,p是节点下标
 59 {
 60     if(LTnode[p].c==0)  //当前节点的颜色为0，即没有颜色
 61         return;
 62     if(LTnode[p].c>0&&!tagcol[LTnode[p].c])  //当前节点有某种颜色并且该颜色没有被计算过
 63     {
 64         cnt++;  //颜色计数器+1
 65         tagcol[LTnode[p].c]=true;
 66         return;
 67     }
 68     if(LTnode[p].c==-1)  //多色 则继续细化处理左右孩子
 69     {
 70         query(p<<1);
 71         query(p<<1|1);
 72     }
 73     return;
 74 
 75 }
 76 
 77 int main()
 78 {
 79     int T;
 80     scanf("%d",&T);
 81     while(T--)
 82     {
 83 
 84         memset(tagcol,false,sizeof(tagcol));
 85         memset(dis,0,sizeof(dis));
 86 
 87         int n;   //n表示有几张海报
 88         //cin>>n;
 89         scanf("%d",&n);
 90         int maxp=0;
 91         for(int i=0;i<n;i++)
 92         {
 93             //cin>>ee[i][0]>>ee[i][1];
 94             scanf("%d%d",&ee[i][0],&ee[i][1]);  //poj上用scanf就过，cin就TLE 坑啊...
 95             if(!dis[ee[i][0]])   //用dis数组先标记下 有没有重复的数据 这样就不用再开一个数组了
 96             {
 97                 e[maxp++]=ee[i][0];
 98                 dis[ee[i][0]]=1;
 99             }
100             if(!dis[ee[i][1]])
101             {
102                 e[maxp++]=ee[i][1];
103                 dis[ee[i][1]]=1;
104             }
105         }
106         memset(dis,0,sizeof(dis));
107         int has=0;
108         sort(e,e+maxp);   //先排序
109         for(int i=0;i<maxp;i++)  //for循环出来后 has 就是离散后的最大范围
110         {
111             dis[e[i]]=++has;
112         }
113         build(1,1,has);
114         for(int i=0;i<n;i++)   //一次插入颜色，i为颜色
115         {
116             update(1,i+1,dis[ee[i][0]],dis[ee[i][1]]);
117         }
118         cnt=0;
119         query(1);
120         cout<<cnt<<endl;
121 
122     }
123 
124     return 0;
125 }

View Code

手打真累啊，肩膀疼..

posted on 2016-08-01 13:58 北溟有鱼。阅读(263) 评论(0) 编辑收藏举报