备忘
写一篇博客备忘，以后应该会渐渐加一些东西。
关于组合数的一些公式
$$\sum_{i=0}^{n}C_{n}^{i}*C_{m}^{i+k}=\sum_{i=0}^{n}C_{n}^{n-i}*C_{m}^{i+k}=C_{n+m}^{n+k}$$
相当于把n+m个物品分两半，枚举前一半和后一半分别选了什么，一共选n+k个的方案数
期望
$E(x^p)=\frac{1}{p+1}$
卡特兰数
$f(n)=C_{2n}^{n}-C_{2n}^{n+1}=\frac{1}{n+1}\times C_{2n}^{n}$
相当于包含$2n$个括号合法的括号序列，或n个节点二叉树的个数。
证明：
左括号为$0$,右括号为$1$，一个合法的括号序列即为任意前缀$0$的个数大于$1$的个数。
一个非法序列一定在某一个最短前缀中$1$的个数刚好等$0$的个数加$1$。
那么把这个前缀$01$取反，就变成了$n+1$个$0$和$n-1$个$1$。
方案数就为$C_{2n}^{n-1}$。
这是一个一一对应关系，每个由$n+1$个$0$和$n-1$个$1$构成的序列一定可以找到第一个$0$大于$1$的位置，$01$翻转后就对应着一个违法原数列。
prufer数列
$n$个节点的生成树个数为$n^{n-2}$
一棵树的prufer数列中每个点出现了$d[i]-1$次，d[i]为点的度数
一种生成Prufer序列的方法是迭代删点，直到原图仅剩两个点。对于一棵顶点已经经过编号的树T，顶点的编号为{1,2,...,n}，在第i步时，移去所有叶子节点（度为1的顶点）中标号最小的顶点和相连的边，并把与它相邻的点的编号加入Prufer序列中，重复以上步骤直到原图仅剩2个顶点。
设{a1,a2,..an-2}为一棵有n个节点的树的Prufer序列，另建一个集合G含有元素{1..n}，找出集合中最小的未在Prufer序列中出现过的数，将该点与Prufer序列中首项连一条边，并将该点和Prufer序列首项删除，重复操作n-2次，将集合中剩余的两个点之间连边即可。
找环
对于一个连通无向图，求出一棵生成树，再判断所有的返祖边就可以找出所有的有用的奇环和偶环。
对于无向图的一些特殊的图论问题通常求任意一棵生成树会很有用。
第二类斯特林数
第二类Stirling数表示将n个不同的元素拆分成m个集合的方案数。
递推式：
$$S(n,m)=\frac{1}{m!}\times \sum_{i=0}^{m}(-1)^k\times C_m^k\times (m-k)^n$$
化简后变成一个卷积的形式，可以NTT快速求出$S(n,1)$到$S(n,n)$.
真·欧几里得算法 直线下整点数目
$$\sum_{0<=x<n} \lfloor \frac{ax+b}{c} \rfloor=n*\lfloor \frac{b}{c} \rfloor+\frac{n*(n-1)}{2}*\lfloor \frac{a}{c} \rfloor+\sum_{0<=x<\lfloor \frac{(a\%c)*n+b\%c\quad}{c} \rfloor} \lfloor \frac{cx+(an+b)\%c}{a\%c} \rfloor$$
第一个式子相当于求ax+b这条直线从0到n-1下整点的数目。
b%c*n相当于把直线下的一个矩形取掉。
(a%c)*(n*(n-1)/2)相当于把直线斜率变到1以下，把上边的点都取掉。
然后变换坐标系，以直线x=n与现在这条直线最靠上的一个交点为原点，向下为x轴，向左为y轴，显然斜率变成了相反数，(a%c)/c--->c/(a%c)。
然后解出直线截距（大概算出之前y方向上最后一小段再乘一下斜率）。
递归计算，当n==0时结束，或an+b<c时结束。
复杂度
$$\sum_{d \mid n}fac(d)$$，其中fac(d)表示d的因子个数,这个东西比n小
指标
在%p的意义下，设x为p的原根，那么对于一个在[1,p-1]中的数a。
$x^y=a$那么y为a的指标。
即可以用加法代替乘法，相当于取对数。
0没有指标，1的指标为0，指标范围为[0,p-2]
线性求逆
$$inv[i]=-(\frac{p}{i})\times inv[p\%i]$$
平面图性质
边数<=3n+6
二分图最小字典序完备匹配
跑两遍匈牙利算法，第一遍求出任意一个完备匹配，第二遍对于每个点贪心选最小的出边判断能否找到不影响前面点的交错环
费用流负环
如果连反向边之前没有负环，那么跑dinic的时候也不会出现负环。
一个NB的思想(很容易忘掉)
一些题可以对于$>=\sqrt{n}$的和$<=\sqrt{n}$的分开讨论,把复杂度从$n^2$降为$n\sqrt{n}$。
陈老师R老师等式
$d(n)$表示n的约数个数。
$$d(n*m)=\sum_{i|n}\sum_{j|m}[(i,j)]$$
$f(n)$表示n的约数和。
$$f(n*m)=\sum_{i|n}\sum_{j|m}i*\frac{m}{j}[(i,j)]$$
哥德巴赫猜想
任何一个大于等于6的偶数都能拆成两个奇素数之和。在OI的数据范围内成立。
ps：没想到还真有一天会用到
Hook length定理
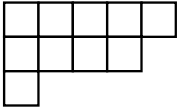
将$1-n$填入格子里，使得每行从左到右递增，每列从上到下递增。
方案数为$\frac{n!}{\Pi{H_{i,j}}}$
$H_{i,j}表示$i,j$这个位置正下和正右加上自己一共有多少格子$
最小二乘法
只能算是这个方法的一个方面吧
当给出一组数据$(x_i,y_i)$,要用一条直线拟合使得误差的平方和最小。
即使$Q=\sum{(y_i-\overline{y_i})^2 }$最小，其中$\overline{y_i}=\beta_1 x_i + \beta_0$\
函数的极值点是在偏导为0的地方
解得(上边是$\beta_1$,下边是$\beta_0$)
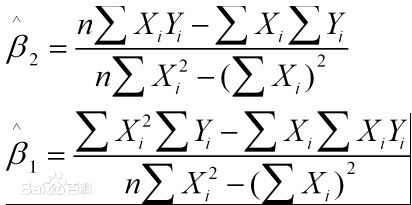
协方差
在概率论和统计学中，协方差用于衡量两个变量的总体误差。
$Cov(x,y)=E[x-E[x]]E[y-E[y]]=E[xy]-E[x]E[y]$
当$x$与$y$无关时，$Cov(x,y)=0$。
$Cov(aX,bY)=abCov(X,Y)$
$Cov(X1+X2,Y)=Cov(X1,Y)+Cov(X2,Y)$。
协方差矩阵
如果$x=(x1,x2,x3,...,xn)^T$为$n$维随机变量
那么$x$的协方差矩阵为
$C=(c_{i,j})_{n \times n},c_{i,j}=Cov(Xi,Xj)$
协方差矩阵可用来表示多维随机变量的概率密度
图的度数序列
