[BZOJ3684][拉格朗日反演+多项式求幂]大朋友和多叉树
题面
Description
我们的大朋友很喜欢计算机科学,而且尤其喜欢多叉树。对于一棵带有正整数点权的有根多叉树,如果它满足这样的性质,我们的大朋友就会将其称作神犇的:点权为\(1\)的结点是叶子结点;对于任一点权大于\(1\)的结点\(u\),\(u\)的孩子数目\(deg_u\)属于集合\(D\),且\(u\)的点权等于这些孩子结点的点权之和。
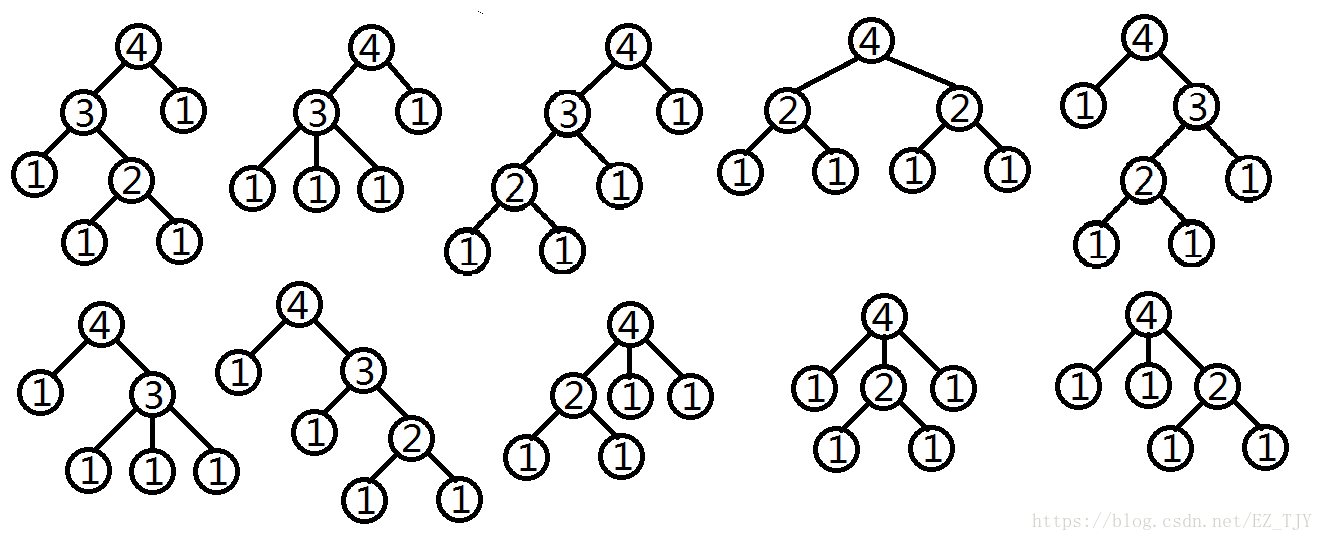
给出一个整数\(s\),你能求出根节点权值为\(s\)的神犇多叉树的个数吗?请参照样例以更好的理解什么样的两棵多叉树会被视为不同的。
我们只需要知道答案关于\(950009857\)(\(453\times2^{21}+1\),一个质数)取模后的值。
Input
第一行有\(2\)个整数\(s,m\)。
第二行有\(m\)个互异的整数,\(d_1,d_2,\ldots,d_m\),为集合\(D\)中的元素。
Output
输出一行仅一个整数,表示答案模\(950009857\)的值。
Sample Input
4 2
2 3
Sample Output
10
HINT
\(1\le m\le s\le10^5,2\le d_i\le s\),有\(3\)组小数据和\(3\)组大数据。
分析
首先,我们设\(v_i\)为集合\(D\)中是否有\(i\)这个元素,有则为\(1\),无则为\(0\):$$v_i=\sum_{k=1}^{m}[d_k=i]$$
我们令\(V(x)\)为\(v_i\)的生成函数:$$V(x)=\sum_{k=0}^\infty v_i x^k$$
我们再设\(f_i\)为根节点权值为\(i\)的神犇多叉树的数量。
首先,显然有\(f_0=0\);而当\(i=1\)即叶子节点时,有\(f_1=1\)。
而在\(i>1\)时,我们枚举根节点的儿子节点数量,在枚举各个叶子节点的权值,根据乘法原理得到递归式:$$f_i=\sum_{k=0}{i-1}v_k\sum_{s_1+s_2+\cdots+s_k=i};;\prod_{j=1}k f_j$$
我们发现后面这个是一个\(k\)重卷积。那么我们令\(F(x)\)为\(f_i\)的生成函数:$$F(x)=\sum_{k=0}^\infty f_k x^k$$
那么我们根据递归式再加上特殊情况时的值,可以得到:$$F(x)=\sum_{k=0}^\infty v_k F(x)^k+x$$
那么我们发现这就是\(V(x)\)的形式。那么我们就得到:$$F(x)=V(F(x))+x$$
即$$F(x)-V(F(x))=x$$
只要我们令\(G(x)=x-V(x)\),就可以构造出一个拉格朗日反演的形式:$$G(F(x))=x$$
那么我们作反演就得到:$$[xn]F(x)=\frac{1}{n}[x]\left(\frac{x}{G(x)}\right)^n$$
即:$$f_s=\frac{1}{s}[x{s-1}]\left(\frac{x}{G(x)}\right)s$$
注意到我们可以\(x\)和\(G(x)\)约掉一个\(x\),则我们令:$$H(x)=\sum_{k=0}^\infty v_{k+1} x^k=\frac{C(x)}{x}$$
则有:$$f_s=\frac{1}{s}[x{s-1}]\left(\frac{1}{1-H(x)}\right)n$$
我们直接多项式求逆+多项式求幂就可以解决了。
关于拉格朗日反演、多项式的操作,详见我的这篇博客:多项式全家桶
代码
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
typedef long long ll;
const ll p=950009857,g=7;
int n,nn,s,m,r[262145];
ll inv[262145],c[262145],gn[2][262145],ans;
inline ll pow(ll a,int b){
ll ans=1;
while(b){
if(b&1)ans=ans*a%p;
a=a*a%p;
b>>=1;
}
return ans;
}
inline ll add(ll a,ll b){return a+b>p?a+b-p:a+b;}
inline ll cut(ll a,ll b){return a-b<0?a-b+p:a-b;}
void init(){
for(n=1;n<=s;n<<=1);
nn=n;
gn[0][0]=gn[1][0]=1;
gn[0][1]=pow(g,(p-1)/(n<<1));
gn[1][1]=pow(gn[0][1],p-2);
for(int i=2;i<(n<<1);i++){gn[0][i]=gn[0][i-1]*gn[0][1]%p;gn[1][i]=gn[1][i-1]*gn[1][1]%p;}
inv[1]=1;
for(int i=2;i<=(n<<1);i++)inv[i]=inv[p%i]*(p-p/i)%p;
}
void NTT(ll c[],int n,int tp=1){
for(int i=0;i<n;i++){
r[i]=(r[i>>1]>>1)|((i&1)*(n>>1));
if(i<r[i])swap(c[i],c[r[i]]);
}
for(int i=1;i<n;i<<=1){
for(int j=0;j<n;j+=(i<<1)){
for(int k=0;k<i;k++){
ll x=c[j+k],y=gn[tp!=1][nn/i*k]*c[j+k+i]%p;
c[j+k]=add(x,y);
c[j+k+i]=cut(x,y);
}
}
}
}
void INTT(ll c[],int n){
NTT(c,n,-1);
for(int i=0;i<n;i++)c[i]=c[i]*inv[n]%p;
}
void inverse(ll c[],int n=n){
static ll t[262145],tma[262145];
t[0]=pow(c[0],p-2);
for(int k=2;k<=n;k<<=1){
for(int i=0;i<(k<<1);i++)tma[i]=(i<k?c[i]:0);
for(int i=(k>>1);i<(k<<1);i++)t[i]=0;
NTT(tma,k<<1);
NTT(t,k<<1);
for(int i=0;i<(k<<1);i++)t[i]=cut(add(t[i],t[i]),t[i]*t[i]%p*tma[i]%p);
INTT(t,k<<1);
}
memcpy(c,t,sizeof(ll)*n);
}
void derivative(ll c[],int n=n){for(int i=0;i<n;i++)c[i]=c[i+1]*(i+1)%p;}
void integrate(ll c[],int n=n){for(int i=n-1;i>=1;i--)c[i]=c[i-1]*inv[i]%p;c[0]=0;}
void ln(ll c[],int n=n){
static ll t[262145];
for(int i=0;i<(n<<1);i++)t[i]=(i<n?c[i]:0);
derivative(t,n);
inverse(c,n);
NTT(t,n<<1);
NTT(c,n<<1);
for(int i=0;i<(n<<1);i++)c[i]=c[i]*t[i]%p;
INTT(c,n<<1);
for(int i=n;i<(n<<1);i++)c[i]=0;
integrate(c,n);
}
void exp(ll c[]){
static ll t[262145],ta[262145];
t[0]=1;
for(int k=2;k<=n;k<<=1){
for(int i=0;i<(k<<1);i++)ta[i]=t[i];
ln(ta,k);
for(int i=0;i<k;i++)ta[i]=cut(c[i],ta[i]);
ta[0]++;
NTT(t,k<<1);
NTT(ta,k<<1);
for(int i=0;i<(k<<1);i++)t[i]=t[i]*ta[i]%p;
INTT(t,k<<1);
for(int i=k;i<(k<<1);i++)t[i]=0;
}
memcpy(c,t,sizeof(ll)*n);
}
void pow(ll c[],int k){
ln(c);
for(int i=0;i<n;i++)c[i]=c[i]*k%p;
exp(c);
}
int main(){
scanf("%d%d",&s,&m);
for(int i=1;i<=m;i++){
int x;
scanf("%d",&x);
c[x-1]=p-1;
}
c[0]=1;
init();
inverse(c);
pow(c,s);
printf("%lld\n",c[s-1]*inv[s]%p);
}