三分

昨天晚修的时候在看必修五，看到线性规划，然后就在想直线相交的问题，然后不知道怎么做，就问hqm大佬，他说用三分，于是就去看了看三分，发现这是一个好东西啊！

我们可以先看下三分最最基本的用法

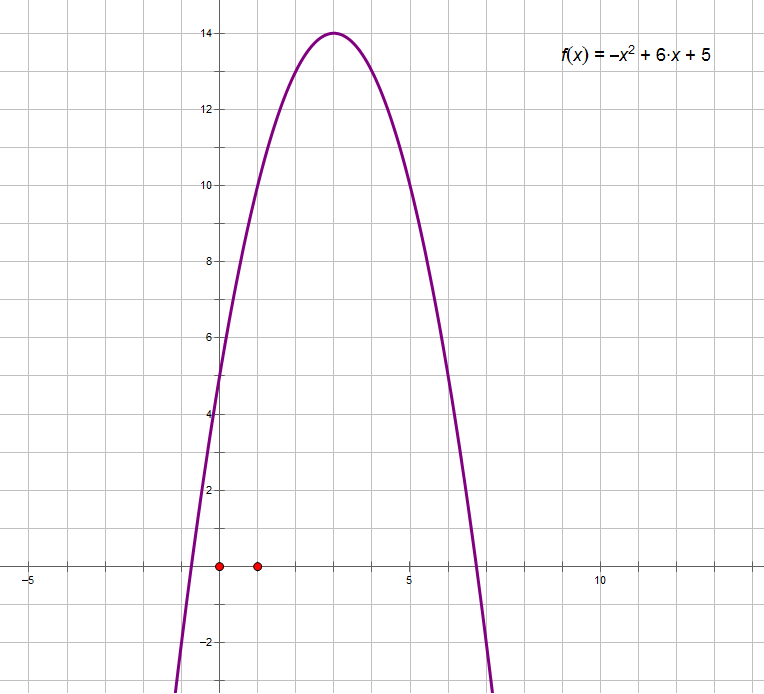
上图显然是一个单峰函数，如果我们要求它的峰值，显然我们找不到高效的算法，这时我们就要用三分了。

1、思路

三分法其实就是二分的升级，二分分成左右两段，而三分分成左中右三段，二分只有中点，而三分有左右两个三等分点（下文记左三等分点记为\(trip_l\),右三等分点记为\(trip_r\)）。

如果\(f(trip_l)>f(trip_r)\)的话那么\(R=trip_r\)否则\(L=trip_l\)

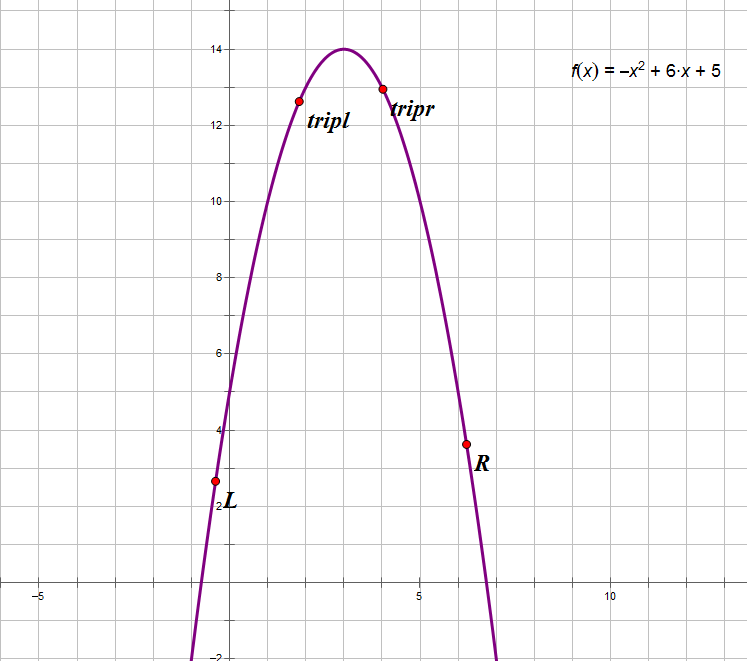
这样我们的思路就极其清晰了

2、代码实现

这里我们就以Luogu P3382 【模板】三分法为例来看下三分法的具体实现。

#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;

const double eps=1e-7;

int n;
double l,r,a[101];

double check(double x){
	double ret=a[0],tmp=x;
	for(int i=1;i<=n;i++){
		ret+=a[i]*tmp;
		tmp*=x;
	}
	return ret;
}

int main(){
	scanf("%d%lf%lf",&n,&l,&r);
	for(int i=n;i;i--){
		scanf("%lf",&a[i]);
	}
	while(r-l>eps){
		double tmp=(r-l)/3.0;
		double l1=check(l+tmp),r1=check(r-tmp);
		if(l1>r1)r=r-tmp;
		else {
			l=l+tmp;
		}
	}
	printf("%.5lf",l);
	return 0;
}