线段树
没错则就是一个(过去的)线段树黑洞的线段树博客
线段树:
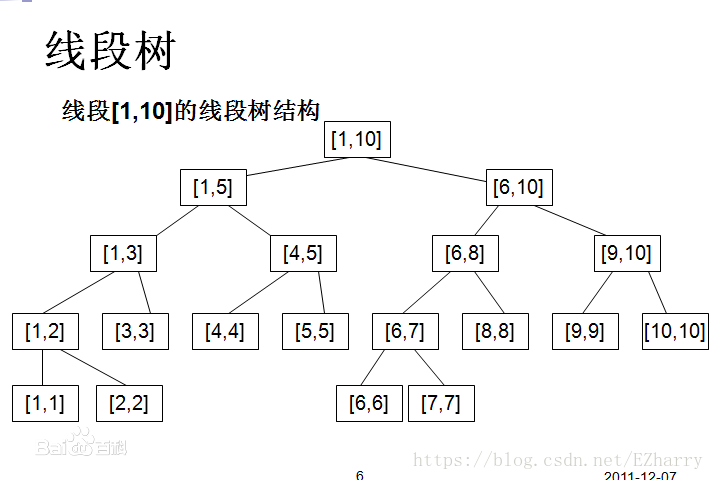
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,实际应用时一般还要开4N的数组以免越界,因此有时需要离散化让空间压缩。
先上一个点修改的模板
忠诚改
tips:这不是洛谷P1816喔(但是用那个测程序也是可以的
Time Limit: 1000 ms Memory Limit: 128 MB
老管家是一个聪明能干的人。他为财主工作了整整10年,财主为了让自已账目更加清楚。要求管家每天记k次账,由于管家聪明能干,因而管家总是让财主十分满意。但是由于一些人的挑拨,财主还是对管家产生了怀疑。于是他决定用一种特别的方法来判断管家的忠诚,他把每次的账目按1,2,3…编号,然后不定时的问管家问题,问题是这样的:在a到b号账中最少的一笔是多少?为了让管家没时间作假他总是一次问多个问题。
在询问过程中账本的内容可能会被修改
Input
输入中第一行有两个数m,n表示有m(m<=100000)笔账,n表示有n个问题,n<=100000。
接下来每行为3个数字,第一个p为数字1或数字2,第二个数为x,第三个数为y
当p=1 则查询x,y区间
当p=2 则改变第x个数为y
Output
输出文件中为每个问题的答案。具体查看样例。
Sample Input
10 3
1 2 3 4 5 6 7 8 9 10
1 2 7
2 2 0
1 1 10
Sample Output
2 0
上代码
#include<iostream> #include<cstdio> using namespace std; int sum[10000001],n,m; void build(int l,int r,int o){ if(l==r){ int x; scanf("%d",&x); sum[o]=x; return; } int mid=(l+r)>>1; build(l,mid,o<<1); build(mid+1,r,(o<<1)+1); sum[o]=min(sum[o<<1],sum[(o<<1)+1]); } void insert(int l,int r,int x,int o,int v){ if(l==r){ sum[o]=v; return; } int mid=(l+r)>>1; if(x<=mid)insert(l,mid,x,o<<1,v); else insert(mid+1,r,x,(o<<1)+1,v); sum[o]=min(sum[o<<1],sum[(o<<1)+1]); } int query(int l,int r,int x,int y,int o){ if(x<=l and r<=y){ return sum[o]; } int mid=(l+r)>>1,ans=0x7fffffff; if(x<=mid)ans=query(l,mid,x,y,o<<1); if(y>mid) ans=min(ans,query(mid+1,r,x,y,(o<<1)+1)); return ans; } int main(){ scanf("%d%d",&n,&m); build(1,n,1); for(int i=1;i<=m;i++){ int x; scanf("%d",&x); if(x==1){ int y,z; scanf("%d%d",&y,&z); printf("%d\n",query(1,n,y,z,1)); }else if(x==2){ int y,z; scanf("%d%d",&y,&z); insert(1,n,y,1,z); } } return 0; }
以上的代码十分(逃XDDD
实际上这个线段树是十分的简(fu)单(za)的
分别有以下几个函数:
build:构建整棵线段树
pushup:对于我们所要求的答案进行往上更新
pushdown:lazy标记下传
update:区间修改(可以当做单点修改用)
query:区间查询(和,最值等)
先上一个丑陋的线段树 
对于每一个颜色的方块,它是线段树上的一个节点
而[x,y]就是x到y的一个闭区间。
所以这里每个节点可以维护一个值(如区间最值、和等
所以我们正式来学习一下区间修改的线段树,刚刚那是点修改的线段树,在oi使用中用处十分有限,同时也可是用区间修改的线段树代替
所以
我们来了解一下各个函数的用法:
build:构建一棵线段树
update:上传(修改)一个区间(点)的值,可以至此区间加、减、set等操作
query:查询一个区间的最值,和等
pushdown:下传lazytag
简述一下lazytag
我们也会发现有时候我们修改是一个区间,而这个区间在线段树上有一个节点刚好被这个区间所包括,那么我们就直接在这个节点上打标记也就是lazytag,我们就不用下传到叶子节点,这样我们就可以省下很大的复杂度。当然我们在查询时也要下放标记。也就是一个懒惰的思想,我们可以先不下放标记,在需要使用时再下放标记。
接下来我们以luogu P3372 【模板】线段树 1 为例
这是线段树最基础的一题
可能大家对于lazytag还是有一定的陌生,但是慢慢就会熟悉的
#include<iostream> #include<cstdio> #define ll long long using namespace std; ll a[100001],sum[400001],lazy[400001]; int n,m; void pushdown(int o,int len){ if(lazy[o]){ int left=o<<1,right=left+1; lazy[left]+=lazy[o],lazy[right]+=lazy[o]; sum[left]+=lazy[o]*(len-(len>>1)); sum[right]+=lazy[o]*(len>>1); lazy[o]=0; } } void build(int o,int l,int r){ if(l==r){ scanf("%d",&sum[o]); return; } int mid=(l+r)>>1,left=o<<1,right=left+1; build(left,l,mid),build(right,mid+1,r); sum[o]=sum[right]+sum[left]; } void update(int o,int l,int r,int x,int y,int v){ if(x<=l and r<=y){ lazy[o]+=v; sum[o]+=v*(r-l+1); return; } int mid=(l+r)>>1,left=o<<1,right=left+1; pushdown(o,r-l+1); if(x<=mid)update(left,l,mid,x,y,v); if(y>mid)update(right,mid+1,r,x,y,v); sum[o]=sum[left]+sum[right]; } ll query(int o,int l,int r,int x,int y){ if(x<=l and r<=y){ return sum[o]; } int mid=(l+r)>>1,left=o<<1,right=left+1; ll m=0; pushdown(o,r-l+1); if(x<=mid)m+=query(left,l,mid,x,y); if(mid+1<=y)m+=query(right,mid+1,r,x,y); return m; } int main(){ scanf("%d%d",&n,&m); build(1,1,n); for(int i=1;i<=m;i++){ int x; scanf("%d",&x); if(x==1){ int y,z,q; scanf("%d%d%d",&y,&z,&q); update(1,1,n,y,z,q); } if(x==2){ int y,z,q; scanf("%d%d",&y,&z); printf("%lld\n",query(1,1,n,y,z)); } } return 0; }
线段树其实我们还有别的操作,如区间乘,set,lca,gcd等等
我们可以看下luogu线段树2
代码
#include<cstdio> #include<cstring> #define ls o*2 #define rs o*2+1 using namespace std; int n,m,Mod; long long lazy1[500001],lazy2[500001],sum[500001],a[100001]; void pushdown(int o,int l,int r){ if(lazy2[o]!=1){ int mid=(l+r)/2; lazy2[ls]=(lazy2[ls]*lazy2[o])%Mod; lazy2[rs]=(lazy2[rs]*lazy2[o])%Mod; lazy1[ls]=(lazy1[ls]*lazy2[o])%Mod; lazy1[rs]=(lazy1[rs]*lazy2[o])%Mod; sum[ls]=(sum[ls]*lazy2[o])%Mod; sum[rs]=(sum[rs]*lazy2[o])%Mod; lazy2[o]=1; } if(lazy1[o]){ int mid=(l+r)/2; lazy1[ls]=(lazy1[ls]+lazy1[o])%Mod; lazy1[rs]=(lazy1[rs]+lazy1[o])%Mod; sum[ls]=(sum[ls]+lazy1[o]*(mid-l+1))%Mod; sum[rs]=(sum[rs]+lazy1[o]*(r-mid))%Mod; lazy1[o]=0; } } void build(int o,int l,int r){ lazy2[o]=1; if(l==r){ sum[o]=a[l]%Mod; return; } int mid=(l+r)/2; build(ls,l,mid); build(rs,mid+1,r); sum[o]=(sum[ls]+sum[rs])%Mod; } void update(int a,int b,int o,int l,int r,int x){ if(a<=l&&b>=r){ // pushdown(o,l,r); sum[o]=(sum[o]+x*(r-l+1))%Mod; lazy1[o]=(lazy1[o]+x)%Mod; return; } pushdown(o,l,r); int mid=(l+r)/2; if(a<=mid) update(a,b,ls,l,mid,x); if(b>mid) update(a,b,rs,mid+1,r,x); sum[o]=(sum[ls]+sum[rs])%Mod; } void update2(int a,int b,int o,int l,int r,int x){ if(a<=l&&b>=r){ // pushdown(o,l,r); sum[o]=(sum[o]*x)%Mod; lazy2[o]=(lazy2[o]*x)%Mod; lazy1[o]=(lazy1[o]*x)%Mod; return; } pushdown(o,l,r); int mid=(l+r)/2; if(a<=mid) update2(a,b,ls,l,mid,x); if(b>mid) update2(a,b,rs,mid+1,r,x); sum[o]=(sum[ls]+sum[rs])%Mod; } long long query(int a,int b,int o,int l,int r){ if(a<=l&&b>=r) return sum[o]; pushdown(o,l,r); int mid=(l+r)/2; long long qq=0; if(a<=mid) qq=(qq+query(a,b,ls,l,mid))%Mod; if(b>mid) qq=(qq+query(a,b,rs,mid+1,r))%Mod; return qq%Mod; } int main(){ // freopen("testdata.in","r",stdin); // freopen("hehe.txt","w",stdout); // for(int i=1;i<500001;i++) lazy2[i]=1; scanf("%d%d%d",&n,&m,&Mod); for(int i=1;i<=n;i++) scanf("%d",&a[i]); build(1,1,n); for(int i=1;i<=m;i++){ int id,x,y,z; scanf("%d",&id); if(id==1){ scanf("%d%d%d",&x,&y,&z); update2(x,y,1,1,n,z); }else if(id==2){ scanf("%d%d%d",&x,&y,&z); update(x,y,1,1,n,z); }else{ scanf("%d%d",&x,&y); printf("%lld\n",query(x,y,1,1,n)); } // printf("No.%d %d\n",i,query(1,n,1,1,n)); // if(i==1) printf("checks:%d\n",query(1,5,1,1,n)); } }
有时频繁的标记下放会给我们带来极大的常数,于是我们就可以用可持久化线段树,当然初学者可以忽略下面的内容。
线段树的标记永久化
其实线段树的标记永久化是一个非常容易理解的东西,往往我们都会在区间操作时打lazytag,但是在标记下放时会耗费大量的时间,所以我们可以尝试标记永久化,这样我们的就不用下放标记,同时代码也更加简洁,因为我们少了一个pushdown函数,同时出错率也会大大降低。
对于标记永久化,其实和普通线段树比起来,其实差不多
#include<iostream> #include<cstdio> #include<cstring> using namespace std; typedef long long ll; int n,m; ll sum[4000001],tag[4000001]; void pushup(int o){ sum[o]=sum[o<<1]+sum[o<<1|1]; } void build(int o,int l,int r){ if(l==r){ scanf("%lld",&sum[o]); return; } int mid=(l+r)>>1; build(o<<1,l,mid); build(o<<1|1,mid+1,r); pushup(o); } void update(int o,int l,int r,int x,int y,ll v){ sum[o]+=((ll)min(r,y)-(ll)max(x,l)+1)*v; if(x<=l and r<=y){ tag[o]+=v; return; } int mid=(l+r)>>1; if(x<=mid){ update(o<<1,l,mid,x,y,v); } if(y>mid){ update(o<<1|1,mid+1,r,x,y,v); } } ll query(int o,int l,int r,ll tg,int x,int y){ if(x<=l and r<=y){ return sum[o]+(ll)(min(r,y)-max(x,l)+1)*(tg); } int mid=(l+r)>>1; ll ret=0; if(x<=mid){ ret+=query(o<<1,l,mid,tg+tag[o],x,y); } if(y>mid){ ret+=query(o<<1|1,mid+1,r,tg+tag[o],x,y); } return ret; } int main(){ scanf("%d%d",&n,&m); build(1,1,n); for(int i=1;i<=m;i++){ int opt; scanf("%d",&opt); if(opt==1){ int x,y; ll z; scanf("%d%d%lld",&x,&y,&z); update(1,1,n,x,y,z); }else{ int x,y; scanf("%d%d",&x,&y); printf("%lld\n",query(1,1,n,0,x,y)); } } return 0; }

